目录

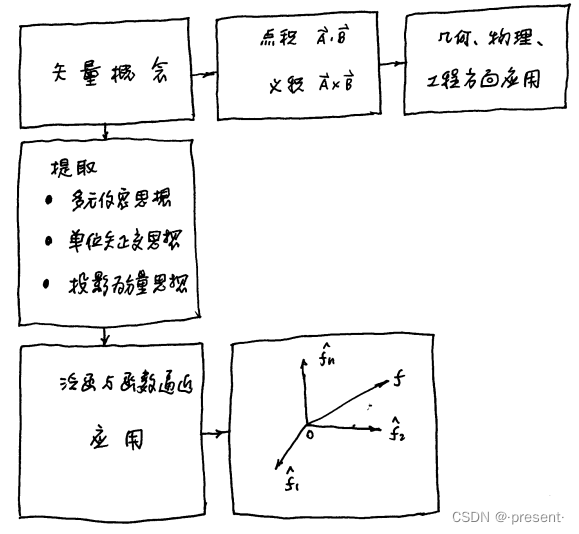
一.什么是矢量

1.1 定义

1.2 公理与体系

1.3 矢量几何化

二.矢量间的相互作用

1.点积

2.点积应用

3.叉积

4. 叉积应用

三.矢量除法

1.单用叉积无法唯一定义矢量除法

2.矢量除法

四.复杂相互作用 

1.混合积

2.双叉积 

3.Laplace公式

五.泛函的广义矢量理论

5.1 投影逼近

5.2 最小二乘法

六.总结 

---

一.什么是矢量

1.1 定义

说起矢量，我们第一想法想到的应该是高中物理所谈到的一个有方向，有大小的量，方向用箭头来

表示，大小则用长度来表示

不过这样的定义，会有点局限，矢量不应该仅仅局限于三维，而可以更高维.

因此，我们给出矢量新的定义.

矢量是有序独立的n个数

比如说我们的邮政编码，这一串数字就可以看作是矢量，它满足有序，独立这两大基本条件.

1.2 公理与体系

有了概念后，我们要建立一个矢量体系，就需要公理作为基石，它是我们建成高楼大厦的基础.

矢量的公理有两个，一个是判断两个矢量是否相等，一个是零矢量.

看似很简单，但是却非常关键，就像1和3不是同一个数字，我们必须事先规定好，同样地，0和零

矢量并不相同，矢量并不是一个简单的数字.

建立公理后，我们需要规定矢量的运算，也就是标题的体系

矢量的体系也有两个，一个是可加性，另一个是可数乘性,两者结合起来，统一称为线性. 

可加性指出两个矢量相加减，是对应位置的元素相加减

PS：可加性符合平行四边形法则，也就是矢量首尾相接，原点指向最后末尾的矢量，即为最终合

成的矢量.

可数乘性指出一个常数和矢量相乘，等于对应每一个位置的元素乘以该常数.（通常我们也把常量

叫做标量scalar，和矢量作区别，常数和标量两者是等价的）

PS：可数乘性，我们也常常把它称作对向量的拉缩，比如乘以2，是将其长度拉长为原来的两倍，

乘以-1/2，则是反向压缩为原来的一半.

1.3 矢量几何化

有了概念，公理和体系，矢量理论可以走出关键的第一步——矢量几何化.

我们将笛卡尔坐标系和单位矢引入.

这样，任意一个三维向量，我们现在就可以通过缩放单位矢，再矢量相加的方法得到它.

比如(3，2，2)一个三维矢量，它的实质就是，将每一个坐标看作一个标量，分别对i,j,k单位矢做缩

放，再相加.(在线性代数中，我们也把n个数乘向量的和，称为这n个向量的线性组合)

一切矢量都可以归功于单位矢，单位矢相当于一个基准的作用，正是由于有了单位矢，我们才可以

用坐标表示一个向量.

我们也可以把它理解为一种运动，首先在x轴坐标轴上移动x个单位，这个单位移动的长度就是我们

单位矢的长度，紧接着沿y轴方向移动y个单位，最后是沿z轴方向，我们就可以得到空间内任意一

个向量.

PS：进一步来说，一个向量可以表示为其模的大小和其方向单位矢的乘积

二.矢量间的相互作用

将矢量在坐标系表示出来后，我们就可以进一步考虑两两向量间的相互作用，一共有两种类型.

1.点积

矢量点积是一种数量型相互作用，顾名思义，得到的结果是一个数

它的定义如下

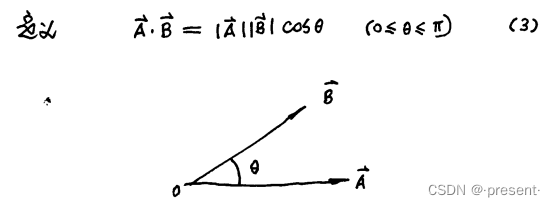
由于它最后得到的结果是一个数，并且结合它的定义，我们可以知道点积是对称运算.

那具体我们如何将矢量点积，表示成坐标系的结果呢？

还是抓住把一切归于单位矢的思想，我们只需要研究透单位矢的点积，就自然而然可以求解任意两

个向量的点积.

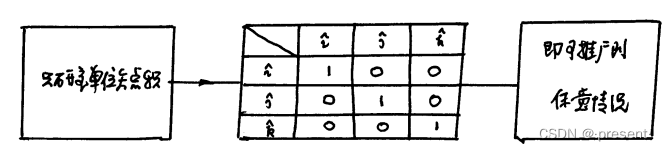
两两相同单位矢做点积结果为1，两两不同单位矢做点积结果为0(i,j,k相互正交， ) 

那对于任意两个向量A,B，由于两两不同单位矢做点积结果为0，与这一项做点积还能剩下

来的，只有对面的，得到，其余全部为0，类似地，我们就可以得到两个向量用坐

标表示后，其点积的运算表达式. 

 

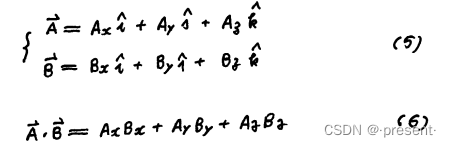
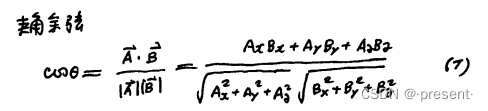
2.点积应用

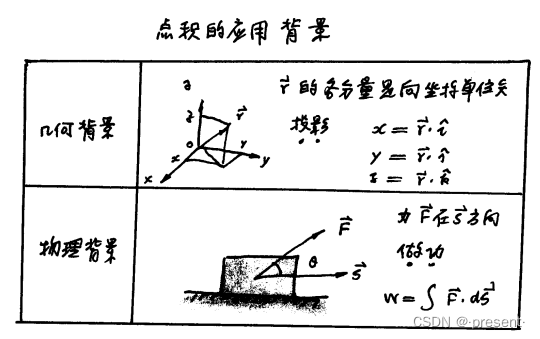
 我们分为两个背景进行讨论，一个是几何背景，一个是物理背景

几何背景，就是我们最常见的投影

将任意向量，和其对应的单位矢做点积，就可以得到其对应坐标值.

把思路放开，不局限于坐标单位矢，而是任意单位矢，其实就可以得到向量沿该单位矢指向方向的

投影

PS：这里能用点积实现投影求坐标，其实隐藏了一个条件，就是坐标单位矢的正交性.

正是i,j,k这三个单位矢两两正交，两两点乘为0，才能实现.

在线性代数里面，也有类似的概念，我们把这三个向量，称作一组基.

基中的任意一个向量，都无法由其余向量线性表示，比如i单位矢，我们不能通过j,k单位矢线性组合得到，我们就称这组向量为线性无关.

基中的每一个向量，都对扩充空间(表示空间中的任意一个向量)发挥作用，正是i,j,k三个正交单位矢缩放再相加，才能表示三维空间中的任意向量.

基的定义:

空间中的一组基是张成该空间的一个线性无关向量组

物理背景，就是我们常见的力对物体做功.

垂直于物体运动方向的力，对物体是不做功的，也就是力对物体做功，需要将力投影到物体运动的

方向，对应的就是力和ds(dl)做点积.

更甚，我们可以用点积证明余弦定理(向量相减，箭头指向被减向量)

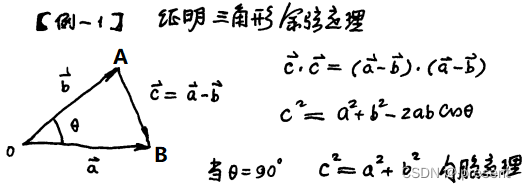
3.叉积

矢量点积是一种矢量型相互作用，顾名思义，得到的结果是一个矢量

既然是矢量，就存在大小和方向

大小与点积相对应，不过，叉积大小乘的是sin

方向符合右手螺旋法则

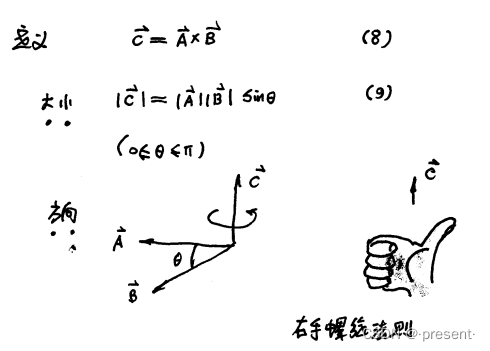
由于它最后得到的结果是一个矢量，并且结合它的定义，我们可以知道点积是反对称运算.(即运算

对象不可随意互换，两者大小相同，但方向不同)

同样的，我们还是抓住把一切归于单位矢的思想，我们只需要研究透单位矢的叉积，就自然而然可

以求解任意两个向量的叉积.

 

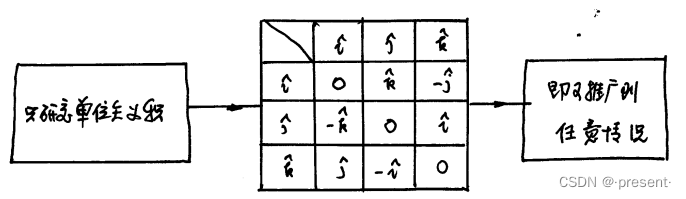
两两相同单位矢做叉积结果为0，两两不同单位矢做叉积得到第三个单位矢，是否带负号，由右手

螺旋法则确定

进一步我们可以总结出行列式法则

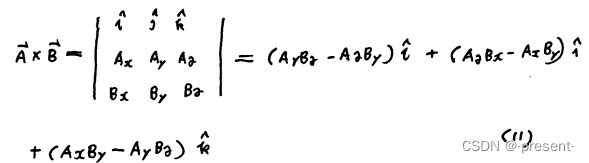
按第一行展开，即可得到对应向量

4. 叉积应用

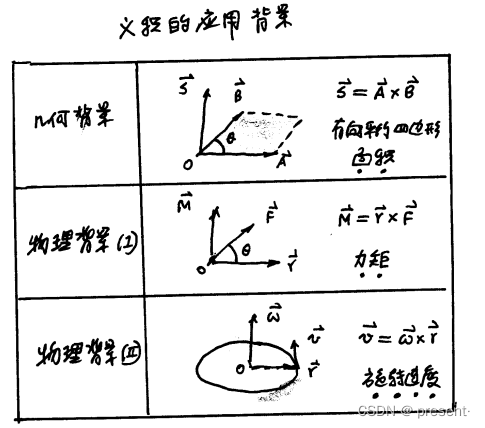
叉积应用同样可以分为几何背景和物理背景进行阐述

几何背景，叉积代表的是有向平行四边形的面积

原因也很简单，因为我们知道平行四边形面积计算的其中一个方法，恰好就是两邻边相乘，再乘以

两者夹角的正弦

物理背景有两个，一个是力矩，用来描述转动的一个矢量

另一个就是我们熟悉的角速度与速度之间的关系式

我们也可以通过叉积证明正弦定理

三.矢量除法

1.单用叉积无法唯一定义矢量除法

讨论到这里，我们有两个方法还没有得到解答

第一，为什么矢量要定义两种运算，点积和叉积?

第二，为什么矢量没有除法?按照一般逻辑，有乘法必定有除法

回答这两个关系之前，我们先看看除法的定义是什么?

已知两个数，分母不为0，两者相除，得到乘法时相乘的那个数，并且该数具有唯一性

 同样的，我们可以假定存在矢量相除这一种运算

那两个矢量相除，得到的应该是一个唯一确定的矢量，和叉乘时的矢量相同

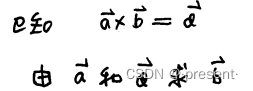
但是，问题就出现了，我们无法唯一性地定义矢量除法

将A,B矢量的叉积用矩阵方式描述，把B矢量中的分量看作未知数，A矢量中的分量看作系数，我们

可以发现系数矩阵的行列式始终为0，系数矩阵不满秩，不是可逆矩阵，方程有无穷多个解

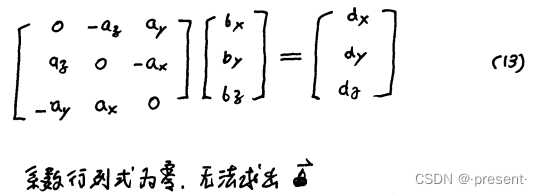
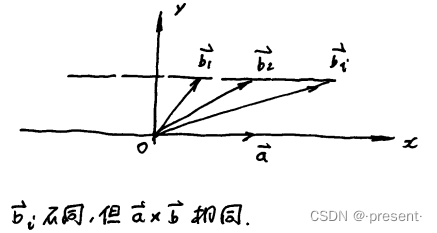
还可以从另一个角度(定义)来看待这个问题

假设我把矢量a放置在x轴，会有无穷多个矢量b，和a做叉乘，得到的都是矢量d(高固定，平行四边

形面积恒定不变)

2.矢量除法

但是引入点积后，我们就可以通过两个矢量点乘和叉乘，唯一确定一个矢量，定义两个矢量的除法

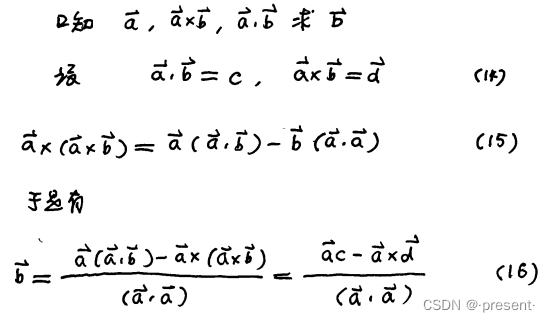
其中式15为双叉乘公式，我们后面会讲解到，公式结果得到的是一个矢量

将式15中的移到左边，左式移到右边，再同时除以这个数字

即可得到矢量b的表达式，由于点积和叉积运算结果都已知，即可以唯一确定b矢量 

总结：

矢量的点乘和叉乘运算并不是孤立的，而是一个有机集合体

按照定义，点积确定一个角的余弦，叉积确定一个角的正弦，其实这个角就唯一确定，两边相同，角确定，自然而然，b矢量其实也就唯一确定

两者满足对偶关系，即一一对应，但又有所差别，比如就拿本质说，一个得到的是数，另一

个得到的是矢量

四.复杂相互作用 

有了两两矢量的相互作用基础，我们便可以考虑更多矢量间的相互作用.

1.混合积

混合积得到的最终结果是一个数，两个向量做叉积得到一个矢量，再与第三个数做点积

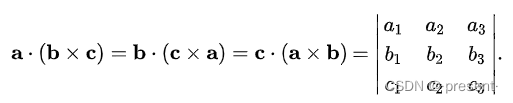
记忆方法也很简单，想象一个循环的圈

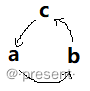
选取哪个矢量作为最后作为最后的点积矢量，然后按逆时针顺序将另外两个矢量做叉积即可.

它的物理背景是两个叉积可以计算得到有向平行四边形面积，另外一个矢量往有向平行四边形方向

做投影，得到的平行六面体体积是不变的 

补充：三个非零矢量混合积为0的充要条件是三个矢量共面(此时平行六面体的体积为0)

2.双叉积 

混合积得到的最终结果是一个矢量，两个向量做点积得到一个数，再与第三个数做数乘

记忆方法就是中间矢量提出来，与剩余矢量的点积做数乘，减去后面矢量提出来，与剩余矢量的的

点积做数乘 

TIPS:

1.点积得到的是一个数，数和矢量做数乘，中间不需要加任何符号(有些网上公式中间加了×

号，没有必要，而且容易造成误导)

2.矢量与矢量间的位置可以互换，因为点积是对称型运算

3.Laplace公式

Laplace公式最终结果是一个数

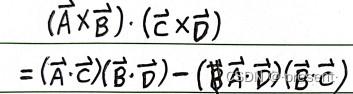
下列是公式的证明

记忆方法也很简单，前前后后做点积，减去左右左右做点积. 

五.泛函的广义矢量理论

把坐标系和单位矢引入矢量体系中，矢量体系得到进一步的发展.

前面我们提到把正交单位矢进行拉缩再相加，可以表示空间中的任意一个向量.

从另一个角度看，我们可以说我们应用正交单位矢来逼近这个矢量.

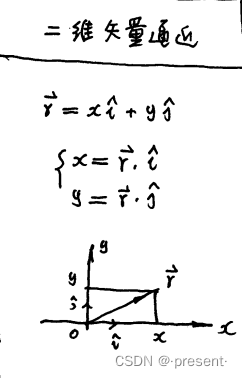
那我们再把思路放开一点，函数能否也像向量一样，逼近一个函数呢？

能否找到类似于正交单位矢概念的正交基函数呢？

答案是可以的，这样我们就可以发展出二维泛函空间.

我们把一族函数，若其满足任意取两个函数相乘并积分为0，则称该族函数为正交函数族.

一个最为常见的正交向量组就是我们的以w为基频率的三角函数族.

傅里叶级数，我们可以从把它看作是正交基函数族逼近某个函数的结果.

逼近函数有两大方法，一是投影逼近，二是最小二乘法

我们接下来将通过一个具体例子，来体会这两种方法.

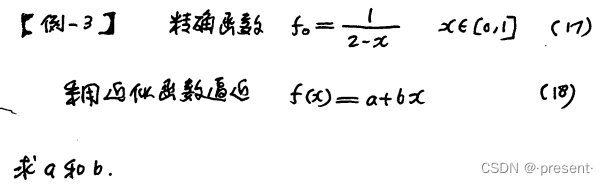
我们现在已知一个具体的精确函数，我们想要通过一个近似线性函数来逼近它，也就是代入不同

的x，所得到的y值尽可能与精确函数算出的y值相同. 

5.1 投影逼近

我们先找两个正交基函数，一个是题目给的近似函数，另一个我们用1来作为正交基函数 

这两个正交基函数需要满足归一性和正交性

所以，我们可以得到两个等式

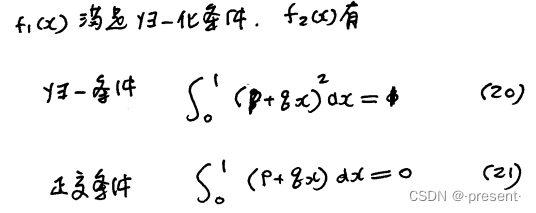
由正交性，我们可以计算得到

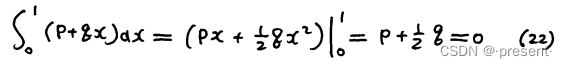
由归一性，我们可以计算得到

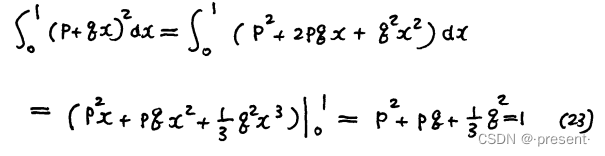
将式22代入式23，即可解出来p和q

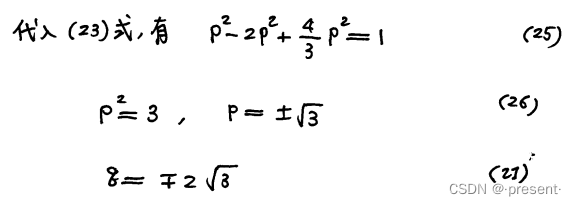
从而确定我们的两个正交基函数

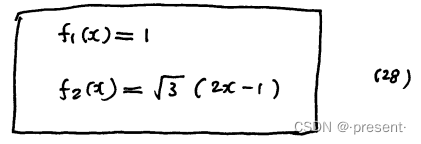
有了正交基函数，我们现在就是求解精确函数，在其上的投影值. 

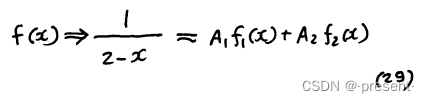
类比于矢量点积投影，函数投影，用的是积分

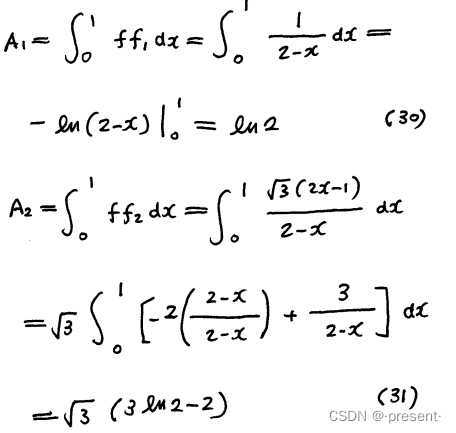
解出来相应的投影值后，我们即可求出近似线性函数

  

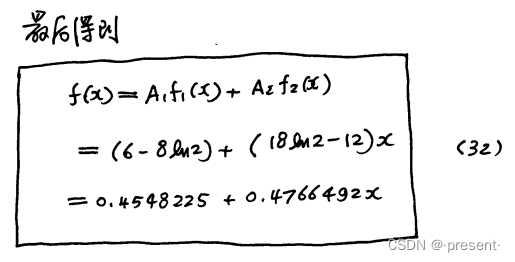
5.2 最小二乘法

必须指出，把函数基推广到广义单位矢的函数逼近思想已经十分普遍，而且它与我们熟悉的最小二

乘法是完全等价的.

最小二乘法的核心思想，就是误差总和最小

我们先假设出该近似线性函数，和原精确函数作差，求误差和，使其最小，便可以得到近似线性函

数

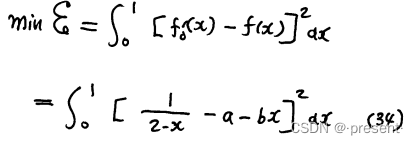
误差式中有a,b两个变量，分别对其求偏导，并使其等于0(b求偏导会有x出)

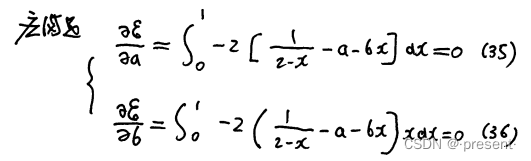
上面式子化简可以得到a,b关系式

 

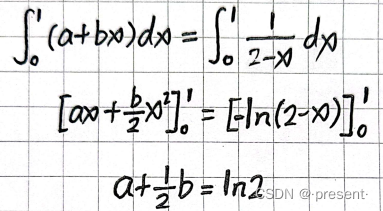
下面式子化简也可以得到a,b关系式

 

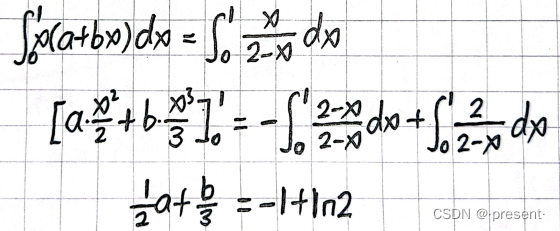
解出来a,b的值，即可得到我们的近似线性函数，可以发现和函数逼近得到的结果完全相同

但是，利用广义单位矢函数逼近的方法并不是最佳逼近，它有局限性

它仅仅是线性逼近，是二维的，只抓了主投影 

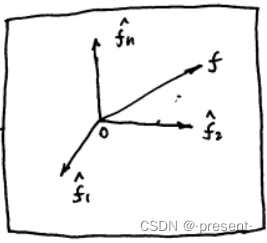
a + bx，仅仅是1，x，还有x的二次，三次，...n次(泰勒级数展开)

六.总结 

紧紧抓住坐标系+单位矢的思想

第一节我们引入了矢量的概念，首先明确了它的两大公理(相等，零矢量)和运算体系(线性)

紧接着我们介绍了它矢量间的相互作用(点积和叉积)，明确定义后，并指出它们的应用

进一步推广到矢量间的相互作用

最后推广到泛函中的广义矢函数，介绍它函数逼近的应用.