前言
参考资料:
高升博客
《CUDA C编程权威指南》
以及 CUDA官方文档
CUDA编程:基础与实践 樊哲勇
文章所有代码可在我的GitHub获得,后续会慢慢更新
文章、讲解视频同步更新公众《AI知识物语》,B站:出门吃三碗饭
在各种设备内存中,全局内存具有最低的访问速度(最高的延迟), 往往是一个CUDA程序性能的瓶颈,所以值得特别地关注。
1:全局内存的合并和非合并访问
关于全局内存的访问模式,有合并(coalesced)与非合并(uncoalesced)之分。合并 访问指的是一个线程束对全局内存的一次访问请求(读或者写)导致最少数量的数据传输,否则称访问是非合并的。
探讨合并度与全局内存访 问模式之间的关系
为简单起见,我们主要以全局内存的读取和仅使用 L2 缓存的情况为例进行下述讨论。 在此情况下,一次数据传输指的就是将 32 字节的数据从全局内存(DRAM)通过 32 字节的 L2 缓存片段(cache sector)传输到SM。
考虑一个线程束访问单精度浮点数类型的全局 内存变量的情形。因为一个单精度浮点数占有 4 个字节,故该线程束将请求 128 字节的数 据。在理想情况下(即合并度为 100% 的情况),这将仅触发 128/32 = 4 次用 L2 缓存的数据传输。那么,在什么情况下会导致多于 4 次数据传输呢?
为了回答这个问题,我们首先需要了解数据传输对数据地址的要求:在一次数据传输 中,从全局内存转移到L2缓存的一片内存的首地址一定是一个最小粒度(这里是32 字节)的整数倍。
例如,一次数据传输只能从全局内存读取地址为 0-31 字节、32-63 字节、64-95字节、96-127 字节等片段的数据。
再接着思考,那么如何保证一次数据传输中内存片段的首地址为最小粒度的整数倍呢? 或者问:如何控制所使用的全局内存的地址呢?答案是:使用CUDA运行时 API 函数(如我们常用的 cudaMalloc)分配的内存的首地址至少是 256 字节的整数倍。
1:顺序的合并访问。我们考察如下的核函数和相应的调用:
void __global__ add(float *x, float *y, float *z) {
int n = threadIdx.x + blockIdx.x * blockDim.x; z[n] = x[n] + y[n];
}
add<<<128, 32>>>(x, y, z);
其中,x、y 和 z 是由 cudaMalloc() 分配全局内存的指针。很容易看出,核函数中对 这几个指针所指内存区域的访问都是合并的。例如,第一个线程块中的线程束将访问 数组x中第 0-31 个元素,对应128字节的连续内存,而且首地址一定是256字节的整数倍。这样的访问只需要 4 次数据传输即可完成,所以是合并访问,合并度为 100%。
案例
本节将通过一个矩阵转置的例子讨论全局内存的合理使用。矩阵转置是线性代数中一 个基本的操作。我们这里仅考虑行数与列数相等的矩阵,即方阵。学完本节后,读者可以思考如何在CUDA中对非方阵进行转置
假设一个矩阵A的矩阵元为Aij,则其转置矩阵B = AT 的矩阵元为

2.1矩阵的复制
__global__ void copy(const real* A, real* B, const int N)
{
const int nx = blockIdx.x * TILE_DIM + threadIdx.x;
const int ny = blockIdx.y * TILE_DIM + threadIdx.y;
const int index = ny * N + nx;
if (nx < N && ny < N)
{
B[index] = A[index];
}
}
const int grid_size_x = (N + TILE_DIM - 1) / TILE_DIM;
const int grid_size_y = grid_size_x;
const dim3 block_size(TILE_DIM, TILE_DIM);
const dim3 grid_size(grid_size_x, grid_size_y);
copy<<<grid_size, block_size>>>(d_A, d_B, N);
注释:
(1)在调用核函数copy时,我们用了二维的网格和线程块。 在该问题中,并不是一定要使用二维的网格和线程块,因为矩阵中的数据排列本质上依然是一维的。然而,在后面的矩阵转置问题中,使用二维的网格和线程块更为方便。
(2)程序中的 TILE_DIM 是一个整型常量,取值为 32,指的是一片(tile)矩阵的维度 (dimension,即行数)。我们将一片一片地处理一个大矩阵。其中的一片是一个 32 × 32 的矩阵。每一个二维的线程块将处理一片矩阵。
(3)和线程块一致,网格也用二维的,维度为待处理矩阵的维度 N 除以线程块维度。
例如,假如N为128,则grid_size_x和grid_size_y都 是 128/32 = 4。也就是说,核函数所用网格维度为 4 × 4,线程块维度为 32 × 32。此时在 核函数 copy 中的 gridDim.x 和 gridDim.y 都等于 4,而 blockDim.x 和 blockDim.y 都等于 32。读者应该注意到,一个线程块中总的线程数目为 1024,刚好为所允许的最大值。
2.1矩阵的转置
if (nx < N && ny < N) B[ny * N + nx] = A[ny * N + nx];
从数学的角度来看,这相当于做了Bij = Aij 的操作。
如果要实现矩阵转置,即Bij = Aji 的 操作,可以将上述代码换成
if (nx < N && ny < N) B[nx * N + ny] = A[ny * N + nx];
or
if (nx < N && ny < N) B[ny * N + nx] = A[nx * N + ny];
注意看其区别变化
以上两条语句都能实现矩阵转置,但是它们将带来不同的性能。
与它们对应的核函数分 别为 transpose1 和 transpose2,代码如下
__global__ void transpose1(const real* A, real* B, const int N)
{
const int nx = blockIdx.x * blockDim.x + threadIdx.x;
const int ny = blockIdx.y * blockDim.y + threadIdx.y;
if (nx < N && ny < N)
{
B[nx * N + ny] = A[ny * N + nx];
}
}
__global__ void transpose2(const real* A, real* B, const int N)
{
const int nx = blockIdx.x * blockDim.x + threadIdx.x;
const int ny = blockIdx.y * blockDim.y + threadIdx.y;
if (nx < N && ny < N)
{
B[ny * N + nx] = A[nx * N + ny];
}
}
可以看出,在核函 数transpose1中,对矩阵A中数据的访问(读取)是顺序的,但对矩阵B中数据的访问(写 入)不是顺序的。
在核函数transpose2中,对矩阵A中数据的访问(读取)不是顺序的,但 对矩阵B中数据的访问(写入)是顺序的。
在不考虑数据是否对齐的情况下,我们可以说核 函数transpose1对矩阵A和B的访问分别是合并的和非合并的,而核函数transpose2对矩阵 A 和 B 的访问分别是非合并的和合并的。
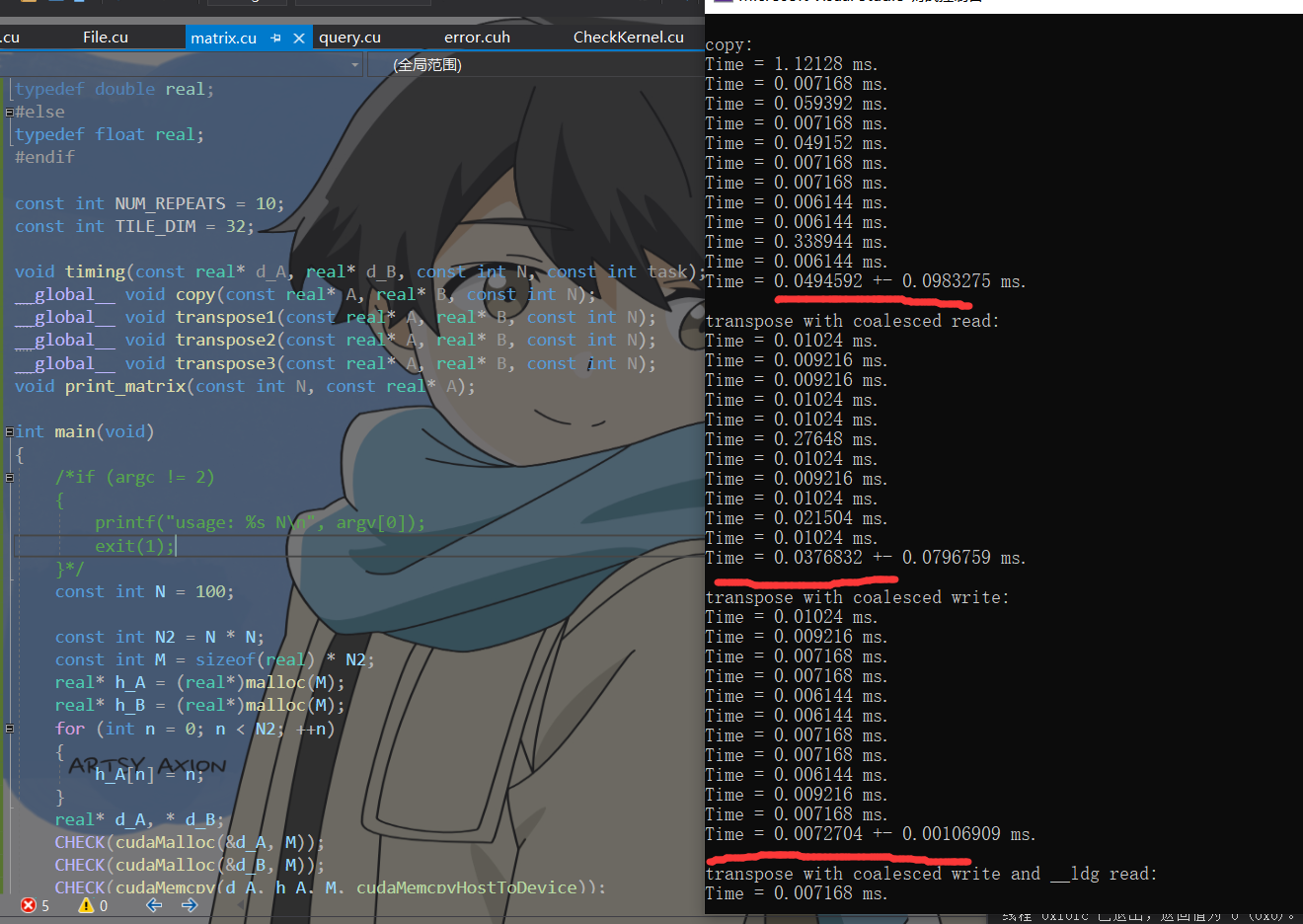
性能结果:
核 函数 transpose1 的执行时间为 5.3 ms,而核函数 transpose2 的执行时间为 2.8 ms。
以上 两个核函数中都有一个合并访问和一个非合并访问,但为什么性能差别那么大呢?
这是因为在核函数transpose2中,读取操作虽然是非合并的,但利用了第 6 章提到的只读数据 缓存的加载函数 __ldg()。从帕斯卡架构开始,如果编译器能够判断一个全局内存变量在 整个核函数的范围都只可读(如这里的矩阵 A),则会自动用函数 __ldg() 读取全局内存, 从而对数据的读取进行缓存,缓解非合并访问带来的影响。对于全局内存的写入,则没有 类似的函数可用。这就是以上两个核函数性能差别的根源。
改进:
所以,在不能同时满足读取和写入都是合并的情况下,一般来说应当尽量做到合并的写入。
#include <stdio.h>
#include <math.h>
#include <stdio.h>
#include<stdint.h>
#include<cuda.h>
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include <stdio.h>
#define CHECK(call) \
do \
{ \
const cudaError_t error_code = call; \
if (error_code != cudaSuccess) \
{ \
printf("CUDA Error:\n"); \
printf(" File: %s\n", __FILE__); \
printf(" Line: %d\n", __LINE__); \
printf(" Error code: %d\n", error_code); \
printf(" Error text: %s\n", \
cudaGetErrorString(error_code)); \
exit(1); \
} \
} while (0)
#ifdef USE_DP
typedef double real;
#else
typedef float real;
#endif
const int NUM_REPEATS = 10;
const int TILE_DIM = 32;
void timing(const real* d_A, real* d_B, const int N, const int task);
__global__ void copy(const real* A, real* B, const int N);
__global__ void transpose1(const real* A, real* B, const int N);
__global__ void transpose2(const real* A, real* B, const int N);
__global__ void transpose3(const real* A, real* B, const int N);
void print_matrix(const int N, const real* A);
int main(void)
{
/*if (argc != 2)
{
printf("usage: %s N\n", argv[0]);
exit(1);
}*/
const int N = 100;
const int N2 = N * N;
const int M = sizeof(real) * N2;
real* h_A = (real*)malloc(M);
real* h_B = (real*)malloc(M);
for (int n = 0; n < N2; ++n)
{
h_A[n] = n;
}
real* d_A, * d_B;
CHECK(cudaMalloc(&d_A, M));
CHECK(cudaMalloc(&d_B, M));
CHECK(cudaMemcpy(d_A, h_A, M, cudaMemcpyHostToDevice));
printf("\ncopy:\n");
timing(d_A, d_B, N, 0);
printf("\ntranspose with coalesced read:\n");
timing(d_A, d_B, N, 1);
printf("\ntranspose with coalesced write:\n");
timing(d_A, d_B, N, 2);
printf("\ntranspose with coalesced write and __ldg read:\n");
timing(d_A, d_B, N, 3);
CHECK(cudaMemcpy(h_B, d_B, M, cudaMemcpyDeviceToHost));
if (N <= 10)
{
printf("A =\n");
print_matrix(N, h_A);
printf("\nB =\n");
print_matrix(N, h_B);
}
free(h_A);
free(h_B);
CHECK(cudaFree(d_A));
CHECK(cudaFree(d_B));
return 0;
}
void timing(const real* d_A, real* d_B, const int N, const int task)
{
const int grid_size_x = (N + TILE_DIM - 1) / TILE_DIM;
const int grid_size_y = grid_size_x;
const dim3 block_size(TILE_DIM, TILE_DIM);
const dim3 grid_size(grid_size_x, grid_size_y);
float t_sum = 0;
float t2_sum = 0;
for (int repeat = 0; repeat <= NUM_REPEATS; ++repeat)
{
cudaEvent_t start, stop;
CHECK(cudaEventCreate(&start));
CHECK(cudaEventCreate(&stop));
CHECK(cudaEventRecord(start));
cudaEventQuery(start);
switch (task)
{
case 0:
copy << <grid_size, block_size >> > (d_A, d_B, N);
break;
case 1:
transpose1 << <grid_size, block_size >> > (d_A, d_B, N);
break;
case 2:
transpose2 << <grid_size, block_size >> > (d_A, d_B, N);
break;
case 3:
transpose3 << <grid_size, block_size >> > (d_A, d_B, N);
break;
default:
printf("Error: wrong task\n");
exit(1);
break;
}
CHECK(cudaEventRecord(stop));
CHECK(cudaEventSynchronize(stop));
float elapsed_time;
CHECK(cudaEventElapsedTime(&elapsed_time, start, stop));
printf("Time = %g ms.\n", elapsed_time);
if (repeat > 0)
{
t_sum += elapsed_time;
t2_sum += elapsed_time * elapsed_time;
}
CHECK(cudaEventDestroy(start));
CHECK(cudaEventDestroy(stop));
}
const float t_ave = t_sum / NUM_REPEATS;
const float t_err = sqrt(t2_sum / NUM_REPEATS - t_ave * t_ave);
printf("Time = %g +- %g ms.\n", t_ave, t_err);
}
__global__ void copy(const real* A, real* B, const int N)
{
const int nx = blockIdx.x * TILE_DIM + threadIdx.x;
const int ny = blockIdx.y * TILE_DIM + threadIdx.y;
const int index = ny * N + nx;
if (nx < N && ny < N)
{
B[index] = A[index];
}
}
__global__ void transpose1(const real* A, real* B, const int N)
{
const int nx = blockIdx.x * blockDim.x + threadIdx.x;
const int ny = blockIdx.y * blockDim.y + threadIdx.y;
if (nx < N && ny < N)
{
B[nx * N + ny] = A[ny * N + nx];
}
}
__global__ void transpose2(const real* A, real* B, const int N)
{
const int nx = blockIdx.x * blockDim.x + threadIdx.x;
const int ny = blockIdx.y * blockDim.y + threadIdx.y;
if (nx < N && ny < N)
{
B[ny * N + nx] = A[nx * N + ny];
}
}
__global__ void transpose3(const real* A, real* B, const int N)
{
const int nx = blockIdx.x * blockDim.x + threadIdx.x;
const int ny = blockIdx.y * blockDim.y + threadIdx.y;
if (nx < N && ny < N)
{
B[ny * N + nx] = __ldg(&A[nx * N + ny]);
}
}
void print_matrix(const int N, const real* A)
{
for (int ny = 0; ny < N; ny++)
{
for (int nx = 0; nx < N; nx++)
{
printf("%g\t", A[ny * N + nx]);
}
printf("\n");
}
}