1. 假设检验
1.1 概述
假设检验是一种统计推断方法,用于对一个或多个总体参数提出关于其取值的假设,并根据样本数据对这些假设进行检验。假设检验的目的是根据样本数据提供统计上的证据,以便对总体参数的假设进行接受或拒绝。
在假设检验中,通常会建立一个原假设H0和一个备择假设H1(或叫做另一种假设)。原假设是对总体参数的陈述,常常是我们希望证明或接受的假设,而备择假设则是对原假设的否定或替代陈述。
1.2 步骤
假设检验的一般步骤如下:
- 建立原假设H0和备择假设H1。
- 选择适当的检验统计量,该统计量应能够反映样本数据对原假设的支持程度。
- 根据显著性水平(通常为0.05)确定拒绝域,拒绝域是检验统计量的取值范围,如果检验统计量的值落在拒绝域内,则拒绝原假设。
- 收集样本数据并计算检验统计量的值。
- 根据检验统计量的值与拒绝域的关系,做出对原假设的判断,即接受或拒绝原假设。
- 给出假设检验的结论,并解释结果的统计显著性和实际意义。
假设检验可以应用于多种情境,例如比较两个或多个总体的均值、比较两个或多个总体的方差、检验相关性等。具体的假设检验方法和统计推断的步骤会根据问题的特点和所采用的统计方法而有所不同。
1.3 示例
洗衣粉标准重量500g,标准差2g。产出的洗衣粉重量为:501.8g、502.4g、499g、500.3g、504.5g、498.2g、505.6g。由此判断这台机器生产的洗衣粉是不是符合要求。
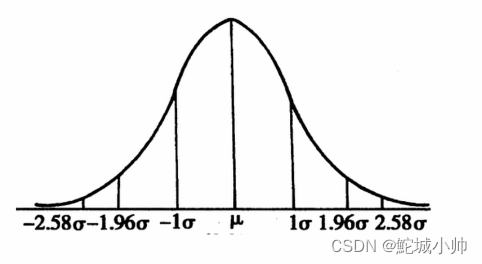
分析过程如下:
- 提供的数据包括洗衣粉的标准重量为500克,标准差为2克,以及实际产出的洗衣粉重量数据。
- 我们希望通过假设检验来判断这台机器生产的洗衣粉是否符合要求。
- 建立原假设H0:样本是符合均值500克,标准差2克的正态分布的。备择假设H1:样本不符合这个分布。
- 根据假设校验量的公式
,计算出检验统计量为2.176。
- 设定显著性水平为0.05。
- 根据显著性水平,查找标准正态分布表或使用统计软件,找到检验统计量为2.176对应的双边P值为约0.026。
- 比较P值(0.026)和显著性水平(0.05)。由于P值小于显著性水平,我们拒绝原假设H0。
- 根据假设检验的结果,得出结论:这台机器生产的洗衣粉不符合标准重量500克,标准差2克的要求。

2. 卡方检验
2.1 概述
卡方检验(Chi-Square Test)是一种用于比较观察值与期望值之间差异的统计检验方法。它适用于分析分类数据的关联性和独立性。
卡方检验的基本思想是比较实际观察值与在假设为真时的期望值之间的差异程度。它通过计算卡方统计量来衡量观察值与期望值之间的差异程度。卡方统计量的计算是基于各个观察值与期望值之间的差异,差异越大,卡方统计量越大,表示观察值与期望值之间的偏离程度越大。
2.2 分析步骤
卡方检验的步骤如下:
(1)建立原假设(H0)和备择假设(H1):
- H0:变量之间不存在关联或独立。
- H1:变量之间存在关联或依赖关系。
(2)构建列联表(Contingency Table):
列联表是将两个或多个分类变量的观察值按照不同组合进行统计汇总的表格。
(3)计算期望值(Expected Values):
根据原假设,计算得到在假设为真时的期望值。
(4)计算卡方统计量(Chi-Square Statistic):
根据观察值与期望值的差异程度,计算得到卡方统计量。
(5)确定自由度(Degrees of Freedom):
自由度是用来描述独立变量中可以自由变动的部分。
(6)确定显著性水平(Significance Level):
选择适当的显著性水平,通常是0.05或0.01。
(7)查找卡方分布表或使用统计软件,根据卡方统计量、自由度和显著性水平,计算得到卡方检验的P值。
(8)比较P值和显著性水平的大小:
- 如果P值小于显著性水平,通常是0.05或0.01,拒绝原假设,认为变量之间存在关联或依赖关系。
- 如果P值大于等于显著性水平,不拒绝原假设,认为变量之间不存在关联或独立。
请注意,卡方检验的应用条件是变量为分类变量,观察值满足一定的条件,例如每个单元格的期望值不小于5等。如果条件不满足,可能需要考虑使用其他适合的检验方法。
2.3 示例
| 男 | 女 | ||
| 化妆 | 15(55) | 95(55) | 110 |
| 不化妆 | 85(45) | 5(45) | 90 |
| 100 | 100 | 200 |
计算公式:
| P | 0.99 | 0.95 | 0.90 | 0.70 | 0.50 | 0.30 | 0.10 | 0.05 | 0.01 |
| 卡方 | 0.00016 | 0.004 | 0.016 | 0.148 | 0.455 | 1.074 | 2.706 | 3.841 | 6.635 |
根据上述的P值与卡方分布对照表,我们可以找到卡方统计量为 129.3 对应的P值。
假设P值取0.05的话,那么卡方值应该不大于3.841的范围,但目前得出的卡方统计量达到了 129.3 。远超过对应的P值0.05对应的3.841,所以,我们可以得出结论:该卡方的P值在显著性水平为 0.05 下,变量之间存在显著关联。
3. 方差检验
3.1 概述
方差检验(Variance Analysis),也称为方差分析或ANOVA(Analysis of Variance),是一种用于比较多个样本均值之间差异的统计方法。它通过分析样本数据的方差来判断各组之间是否存在显著差异。
3.2 使用场景
方差检验适用于以下场景:
- 有一个因变量(连续型)和一个或多个自变量(分类型);
- 自变量有两个以上的水平(组);
- 假设要比较各组均值是否存在显著差异。
方差检验的基本思想是将总体方差分解为组内方差和组间方差,然后通过计算统计量(F值)来比较组间方差和组内方差的大小关系,进而判断各组均值是否存在显著差异。
3.3 检验步骤
方差检验通常包括以下几个步骤:
(1)建立假设:
- H0(原假设):各组样本均值相等,即组间差异为零;
- H1(备择假设):至少有一组样本均值不相等,即组间差异不为零。
(2)计算统计量:
- 组间平方和(SSB):各组均值与总体均值之差的平方和;
- 组内平方和(SSW):各组内观察值与各组均值之差的平方和;
- 组间均方(MSB):组间平方和除以组间自由度;
- 组内均方(MSW):组内平方和除以组内自由度;
- F值:组间均方与组内均方的比值。
(3)确定显著性水平(α)和自由度:
- 显著性水平(α):用于决定拒绝原假设的临界值,常见的显著性水平有0.05和0.01;
- 自由度:组间自由度和组内自由度。
(4)比较F值与临界值:
- 如果计算得到的F值大于临界值,则拒绝原假设,认为各组均值存在显著差异;
- 如果计算得到的F值小于等于临界值,则接受原假设,认为各组均值无显著差异。
(5)计算P值:
- 如果拒绝原假设,则根据F分布表或使用统计软件计算得到P值;
- P值表示观察到的样本结果或更极端结果出现的概率,
3.4 示例
数据分为m组,共n个采样:3组,共15个采样
| 编号 | 电池寿命 | ||
| 甲 | 乙 | 丙 | |
| 1 | 49 | 28 | 38 |
| 2 | 50 | 32 | 40 |
| 3 | 39 | 30 | 45 |
| 4 | 40 | 26 | 42 |
| 5 | 43 | 34 | 48 |
计算:
检验统计量F,做假设检验【F满足自由度(m-1,n-m)的F分布】
假设:
假设三者的均值是一定的,是没有区别的。检验统计量为F值。
| 甲 均值 | 乙 均值 | 丙 均值 | 总体均值 | SSM | SSE |
| 44.2 | 30 | 42.6 | 38.93 | 604.93 | 206 |
F值:
P值:
由此,可以得出,三者是存在差异的,并不是没有差异。(在方差检验中,P值(P-value)表示观察到的样本结果或更极端结果出现的概率。P值越小,表示观察到的差异越显著,即拒绝原假设的程度越高。)