2022年天府杯全国大学生数学建模竞赛
E题 地铁线路的运营与规划
原题再现:
地铁是一种非常绿色快捷的交通出行方式,全国各大城市也都在如火如荼地进行地铁线路建设与规划。但乘坐地铁有时候会感觉特别拥挤,这一时期我们称为高峰期。如何合理安排线路和运营策略是地铁运营者和普通大众都很关心的话题。
我们收集了杭州市三条地铁线路的数据。其中,附件 1 为杭州三条地铁线路首班车、末班车发车时间和站点,附件 2 是杭州市公交站点分布,附件 3 是 2019年 1 月 21 日杭州市各地铁站 24 小时内的人流量数据。由于人流量数据已经经过脱敏处理,无法直接与线路和站点对应,需要你们自行分析。其中字段的意义为:time 是刷卡时间,lineID 是线路,stationID 是站点,deviceID 是刷卡设备,status 中 0 为出站 1 为进站,userID 是用户身份,payType 代表支付方式。目前杭州市线路图如图所示:
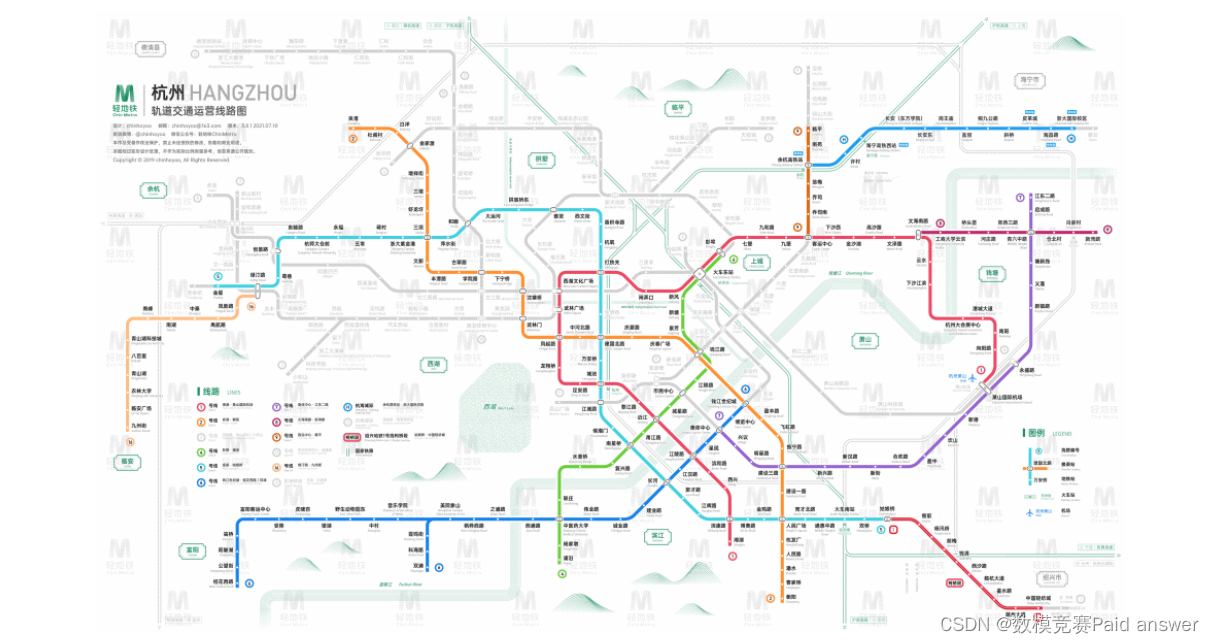
你们需要解决以下问题:
(1) 根据附件 3,请试着预测 1 小时内人 A 线各站点的人流量变化
(2) 根据人流量数据分析,针对这三条地铁线路,发车间隔应如何设置能够避免早高峰晚高峰造成的人流拥堵?
(3) 如果你是地铁运营方,考虑到附件 2 中的公交站点位置与居民下车变更交通方式的便捷性,你会新增哪几条地铁线路?请说明你的理由。
整体求解过程概述(摘要)
针对问题一,首先,将附件 3 进行数据预处理,将线路 A 从多线路中进行分离,然后,对线路 A 中的不同站点进行分离,再将每个站点中的乘客分为进站和出站两类进行分析。其次,分别建立回归预测模型进行分析,得出分析结果,67 站点第 9 小时结果为 730.233,再用指数平滑法模型通过已知数据对未来一小时内人流量进行预测比较,趋势平缓的站点运用一次平滑指数法,呈现二元曲线的站点运用三次平滑指数法预测。最后,运用时间预测模型,可得出 67、68、69 等站点后一小时的人流量分别为 237、8946、410.6 等。
针对问题二,首先,对附件 2 和附件 3 的数据进行处理,通过一天的人流量来判断出地铁的高峰期为每天的 7:00-8:59,设置出发车时间间隔来避免高峰期的拥堵。其次,基于人流量运用粒子群优化算法对发车时间间隔进行优化,不考虑特殊情况,在高峰期缩短发车的时间间隔,最后,运用 Matlab 进行数据处理,计算出优化后的结果,经过计算后得出,在高峰期时将发车的时间间隔改为 3分 40 秒就会避免拥堵。
针对问题三,首先,对轨道交通和接运公交的技术经济特性分析进行分析,比较得出轨道交通的优势,然后,考虑轨道交通选取的因素,建立轨道站点选取模型,分析需要被接运的公交服务的轨道站点,最后,通过计算客流周转量确定站点选取的标准,建立聚集效应函数模型,确定轨道站点合理的接运范围,若地铁晚高峰的客流量为 7019 人,最低换乘人流比率为 85%,最接近的换乘距离就为2.5km,可以据此根据公交站点设置新增地铁站点。
模型假设:
1、假设在设计线路时,不考虑城市空间建设
2、假设车辆发车的时间间隔不变,在沿途各站停车时间固定不变。
3、假设站台与站台之间车辆的运行速度是恒定的,并且在中途无特殊事件发生。
4、假设三条地铁在运行时不会相互影响。
问题分析:
针对问题一:首先,将附件 3 进行数据预处理,将线路 A 进行分离,然后,对线路 A 中的不同站点进行分离,再将每个站点中的乘客分为进出站两类进行分析。其次,分别建立回归预测模型和指数平滑法模型通过已知数据对未来一小时内人流量进行预测比较,得出分析结果。最后,对二者的预测精度进行比较,在实际预测中可以选择更精确的方法。
针对问题二:首先,对附件 2 和附件 3 的数据进行处理,通过一天的人流量来判断出地铁的高峰期,设置出发车时间间隔来避免高峰期的拥堵。其次,基于人流量运用粒子群优化算法对发车时间间隔进行优化,不考虑特殊情况,在高峰期缩短发车的时间间隔,最后,运用 Matlab 进行数据处理,计算出优化后的结果。
针对问题三:首先,对轨道交通和接运公交的技术经济特性分析进行分析,比较得出轨道交通的优势,然后,考虑轨道交通选取的因素,建立轨道站点选取模型,分析需要被接运的公交服务的轨道站点,最后,通过计算客流周转量确定站点选取的标准,建立聚集效应函数模型,确定轨道站点合理的接运范围。
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
clear
clc
S=[13
176
773
1116
3994
265
272
166];
figure
hold on
plot(S,'b-*','linewidth',1);
alpha=0.5;
beta=0.5;
gamma=0.3;
fc=3;%预测个数
k=3;%初始取均值数据个数
n=length(S);
a(1)=sum(S(1:k))/k;
b(1)=(sum(S(k+1:2*k))-sum(S(1:k)))/k;
s=S(1)-a(1);
y=a(1)+b(1)+s(1);
for i=1:n+fc-1
if i==length(S)
S(i+1)=a(end)+b(end)+s(end-k+1);
end
a(i+1)=alpha*(S(i)-s(i))+(1-alpha)*(a(i)+b(i));
b(i+1)=beta*(a(i+1)-a(i))+(1-beta)*b(i);%趋势
s(i+1)=gamma*(S(i)-a(i)-b(i))+(1-gamma)*s(i);%周期
y(i+1)=a(i+1)+b(i+1)+s(i+1);
end
plot(n:n+fc,S(end-fc:end),'r-o','linewidth',1);
legend('历史走势','未来走势')
xlim([0,14])
clear all;
close all;
clc;
N=20; %群体粒子个数
D=3; %粒子维数
T=50; %最大迭代次数
c1=1.5; %学习因子 1
c2=1.5; %学习因子 2
w=0.8; %惯性权重
Xmax=4; %位置最大值
Xmin=1; %位置最小值
Vmax=5; %速度最大值
Vmin=-5; %速度最小值
%初始化个体
x=rand(N,D)*(Xmax-Xmin)+Xmin;
v=rand(N,D)*(Vmax-Vmin)+Vmin;
%初始化个体最优位置和最优值
p=x;
pbest=ones(N,1);
for i=1:N
pbest(i)=func1(x(i,:));
end
%初始化全局最优位置和最优值
g=ones(1,D);
gbest=inf;
for i=1:N
if (pbest(i)<gbest)
g=p(i,:);
gbest=pbest(i);
end
end
gb=ones(1,T);
%按照公式依次迭代直到满足精度或者迭代次数
for i=1:T
for j=1:N
if (func1(x(j,:))<pbest(j))
p(j,:)=x(j,:);
pbest(j)=func1(x(j,:));
end
if (pbest(j)<gbest)
g=p(j,:);
gbest=pbest(j);
end
v(j,:)=w*v(j,:)+c1*rand*(p(j,:)-x(j,:))+c2*rand*(g-x(j,:));
x(j,:)=x(j,:)+v(j,:);
%边界条件处理
for ii=1:D
if (v(j,ii)<Vmin)||(v(j,ii)>Vmax)
v(j,ii)=rand*(Vmax-Vmin)+Vmin;
end
if (x(j,ii)<Xmin)|(x(j,ii)>Xmax)
x(j,ii)=rand*(Xmax-Xmin)+Xmin;
end
end
end
%记录全局最优值
gb(i)=gbest;
end
g; %最优个体
gb(end); %最优值
figure
plot(gb)
xlabel('迭代次数')
ylabel('适应度值')
title('适应度进化曲线')
%适应度函数
function result=func1(x)
summ=sum(x.^2);
result=summ;
end