文章目录
- 前言
- 一、二叉搜索树的概念
- 二、代码详解
- 1、构建节点
- 2、构建二叉树类
- 3、插入方法
- 4、删除方法
- 5、四种遍历方法
- 6、测试代码
- 总结
前言
前文已经讲了二叉树概念,并搞出一个数组存储的没写具体实用意义的二叉树,这篇文章将讲解二叉树的另一种存储方式:链式存储,它和链表的存储方式有点像,这也是前面用了很多篇幅写链表的原因,实现了链表再来看本文会容易很多。因为光写链式存储水一篇文章也太没意义了,所以本文将实现一个链式存储基本有序的二叉搜索树,并实现四种遍历方式,它在排序搜索方面有一定的实用意义。
一、二叉搜索树的概念
我们先给出测试数据 int arr[10] = {5, 3, 6, 8, 9, 2, 4, 7, 10, 1};,还是以一张图来看,比较直观好懂,这张图是最后实现后的效果:
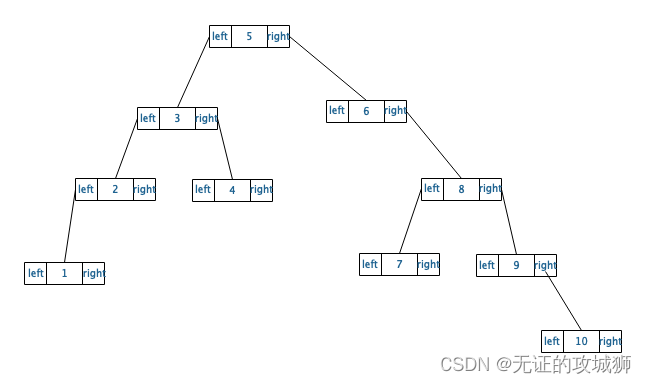
二叉搜索树(BST)是一种基于节点的二叉树数据结构,它具有以下性质:节点的左子树只包含键值小于节点键值的节点;节点的右子树只包含键值大于节点键值的节点;每个节点的左右子树也必须是二叉搜索树。
二叉搜索树支持多种操作,包括搜索、插入和删除。搜索操作通过比较要搜索的值和当前节点的键值来进行。如果要搜索的值小于当前节点的键值,则在左子树中继续搜索;如果要搜索的值大于当前节点的键值,则在右子树中继续搜索。插入操作类似于搜索操作,不同之处在于当找到一个空位置时,新节点将被插入到这个位置。删除操作相对复杂一些,需要考虑被删除节点的子节点数量和位置。下面给出实现代码:
二、代码详解
代码比较长,分段来说吧:
1、构建节点
#include <iostream>
#include <queue>
using std::cout;
using std::endl;
using std::queue;
template <typename T> class Btree; //仅声明,为了下面节点定义友元
template <typename T> class Node{
private:
T val;
Node<T>* left;
Node<T>* right;
public:
friend class Btree<T>;
Node(){
left = nullptr;
right = nullptr;
}
Node(T data){
val = data;
left = nullptr;
right = nullptr;
}
};
以上是节点类,这里直接在节点中写了赋值,比较方便。顺便声明了二叉树类,方便在节点类中写友元。
2、构建二叉树类
template<typename T> class Btree{
private:
Node<T>* root;
public:
Btree(){
root = nullptr;
}
Btree(T data){
root = new Node<T>(data);
}
~Btree(){
deleteTree(root);
}
void deleteTree(Node<T>* node) {
if (node != nullptr) {
deleteTree(node->left);
deleteTree(node->right);
delete node;
}
}
以上是二叉树类的构造、析构函数。因为在节点中写了赋值,这里构造很简单,析构方法调用了一个函数,直接在析构里写循环也是一样的。
3、插入方法
bool insert(T v){
if (!root){
root = new Node<T>(v);
return true;
}
Node<T>* curr = root;
while (curr){
if (v < curr->val){
if (!curr->left){
curr->left = new Node<T>(v);
return true;
}else{
curr = curr->left;
}
}else{
if (!curr->right){
curr->right = new Node<T>(v);
return true;
}else{
curr = curr->right;
}
}
}
return false;
}
以上是插入函数,这个方法逻辑也不复杂,先判断有无根节点,没有就先建立根节点,后面插入的值就是比大小了,小于根节点的放左边,大于根节点的放右边。最终按示例给出的数据,会形成如图所示的结构。仔细想想,并不难理解。
4、删除方法
void remove(T v){
root = remove(root, v);
}
Node<T>* remove(Node<T>* node, T v){
if (node == nullptr) return node;
if (v < node->val) {
node->left = remove(node->left, v);
} else if (v > node->val){
node->right = remove(node->right, v);
} else{
if (node->left == nullptr){
Node<T>* tmp = node->right;
delete node;
return tmp;
} else if (node->right == nullptr){
Node<T>* tmp = node->left;
delete node;
return tmp;
}
Node<T>* tmp = min(node->right);
node->val = tmp->val;
node->right = remove(node->right, tmp->val);
}
return node;
}
Node<T>* min(Node<T>* node){
Node<T>* current = node;
while (current && current->left != nullptr)
current = current->left;
return current;
}
以上是删除方法,这个写法有点绕~ remove这个方法有一个重载,这是因为我们要删除某个节点,却只知道某节点的值,并不知道具体是哪个节点,那就只能从根节点开始找。删除节点有三种情况:
- 如果要删除的节点是叶子节点(没有子节点),则直接删除该节点,这个最简单了。
- 如果要删除的节点只有一个子节点,则用该子节点替换要删除的节点。
- 如果要删除的节点有两个子节点,则用其右子树中的最小值(或左子树中的最大值)替换要删除的节点,然后在右子树(或左子树)中递归删除最小值(或最大值)。这里是以右子树最小值来实现的,这二种方法基本上是一样的逻辑实现,因为这个二叉树是有序的,找起来也很方便。右子树最小值就是该节点的右边的最左边,左子树中的最大值就是该节点的左边的最右边那个节点。
root = remove(root, v); 这行代码调用了它的重载 remove 函数,该函数接受两个参数:一个 Node* 类型的指针和一个 T 类型的值。在这行代码中,第一个参数是 root,表示从树的根节点开始找;第二个参数是 v,它是要删除的节点的值。
remove 函数会返回一个 Node* 类型的指针,表示删除节点后新的根节点。在这行代码中,我们将返回的新根节点赋值给了 root 变量(如果删除的是主根节点),以更新树的根节点。
如果删除的不是主根节点,比如想要删除值为6的节点,那么 remove 函数将首先比较6和根节点的值。如果6大于根节点的值,则函数将在右子树中递归调用自身,以在右子树中查找并删除值为6的节点。
当找到值为6的节点时,函数将检查该节点是否有左子节点。如果没有左子节点,则函数将返回该节点的右子节点,并删除该节点。在这种情况下,返回的 tmp 将是值为6的节点的右子节点。
这样写的目的是为了能够递归地删除节点。在 remove 函数中,我们首先检查要删除的值是否小于当前节点的值,如果是,则在左子树中递归删除;否则,如果要删除的值大于当前节点的值,则在右子树中递归删除。当找到要删除的节点时,我们按前面提到的三种情况之一来删除该节点,并返回新的根节点。
根节点5的右子节点指针在 remove(Node<T>* node, T v) 函数递归返回时被更新。
当 remove(Node<T>* node, T v) 函数递归调用自身以在右子树中查找并删除值为6的节点时,它将返回一个新的子树的根节点。在这种情况下,返回的新根节点是值为6的节点的右子节点,即值为8的节点。
当递归返回到根节点时,我们将更新根节点的右子节点指针,使其指向新的子树的根节点。在这种情况下,我们将根节点的右子节点指针更新为指向值为8的节点。
if (v < node->val){
node->left = remove(node->left, v);
} else if (v > node->val){
node->right = remove(node->right, v);
}
就是这段代码,我们递归地调用 remove 函数,并将返回的新子树的根节点赋值给当前节点的左子节点或右子节点指针。
5、四种遍历方法
void preOrder(Node<T>* p = nullptr){
Node<T>* curr;
if (!p) curr = root;
else curr = p;
if (curr){
cout << curr->val << " ";
if (curr->left) preOrder(curr->left);
if (curr->right) preOrder(curr->right);
}
}
void inOrder(Node<T>* p = nullptr){
Node<T>* curr;
if (!p) curr = root;
else curr = p;
if (curr){
if (curr->left) inOrder(curr->left);
cout << curr->val << " ";
if (curr->right) inOrder(curr->right);
}
}
void postOrder(Node<T>* p = nullptr){
Node<T>* curr;
if (!p) curr = root;
else curr = p;
if (curr){
if (curr->left) postOrder(curr->left);
if (curr->right) postOrder(curr->right);
cout << curr->val << " ";
}
}
void layOrder(){
Node<T>* curr = root;
queue<Node<T>*> q;
int count = 0;
q.push(curr);
count++;
while (q.front()){
curr = q.front();
cout << curr->val << " ";
q.pop();
if (curr->left){
q.push(curr->left);
count++;
}
if (curr->right){
q.push(curr->right);
count++;
}
}
//cout << endl << count << endl; //统计节点数
}
};
上面的代码是四种遍历方式,也是比较好理解的。值得一提的是中序遍历 inOrder 它的输出结果是:
1 2 3 4 5 6 7 8 9 10
也即是说,这个二叉树有排序功能。它的排序效率是O(n)。这个在数据插入的时候就已经排好了。当然这个二叉树主要不是用来排序的,这只是顺便的,它主要用于搜索。因为分了大小,只要根节点选得好,它的效率还是比较高的。但是这个数据结构的效率不稳定,在最差情况下这个结构会变成单向链表。这里笔者是故意把5放在最前面做根节点,演示了这个结构效率比较高的情况。
6、测试代码
int main(){
int arr[10] = {5, 3, 6, 8, 9, 2, 4, 7, 10, 1};
Btree<int> t;
for (int i=0; i<10; ++i) t.insert(arr[i]);
t.remove(6);
t.preOrder();
cout << endl;
t.inOrder();
cout << endl;
t.postOrder();
cout << endl;
t.layOrder();
return 0;
}
按以上代码测试后的结果:
5 3 2 1 4 6 8 7 9 10
1 2 3 4 5 6 7 8 9 10
1 2 4 3 7 10 9 8 6 5
5 3 6 2 4 8 1 7 9 10
//6被删除后:
5 3 2 1 4 8 7 9 10
1 2 3 4 5 7 8 9 10
1 2 4 3 7 10 9 8 5
5 3 8 2 4 7 9 1 10
总结
好了,这篇文章太长了~ 好想拆成两篇啊。好像忘记写查找方法了哈…不过那个逻辑很简单,随便想想也就搞定了,有需要的读者自己搞定吧,预告一下:下一篇会写有序二叉树的扩展功能,比如搜索父节点、子节点、前驱后续节点等。