弗雷歇distanceDTW(动态时间规整)算法（附部分代码）

news2024/11/17 20:51:37

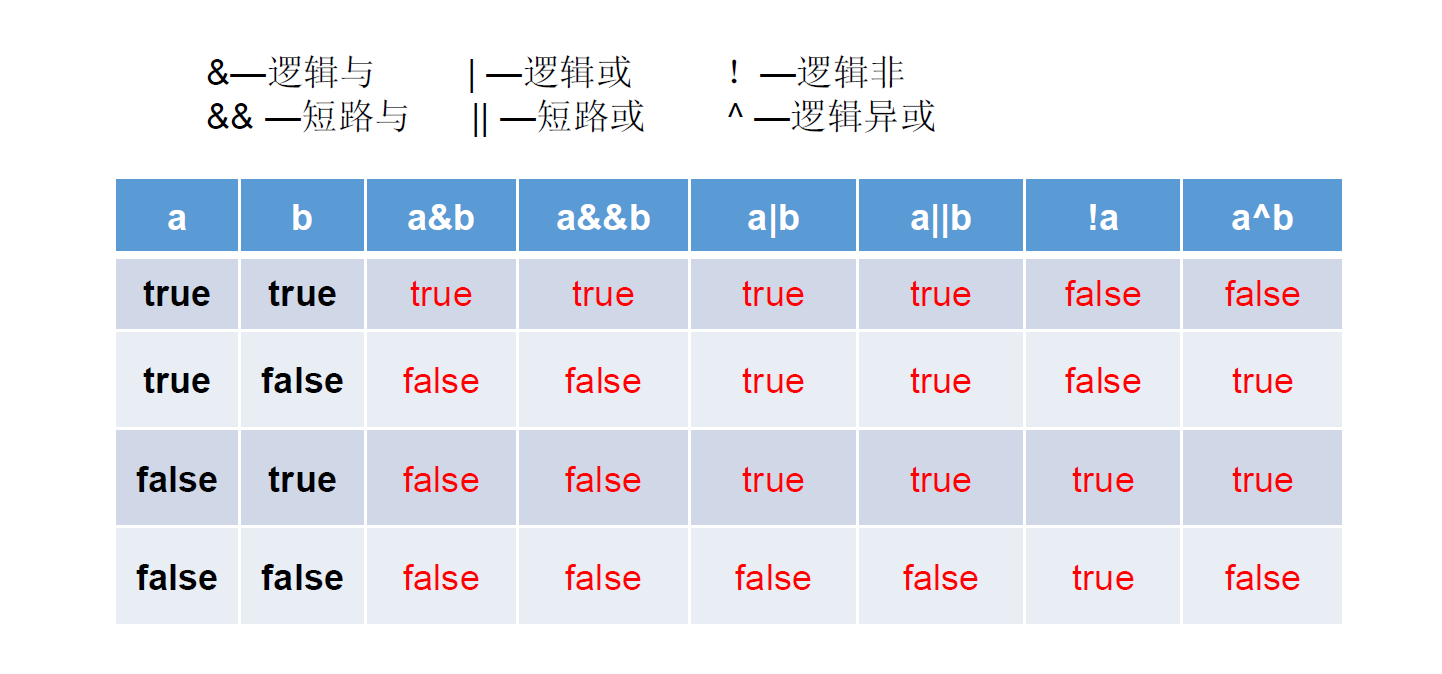
1、理论知识

1.1 什么是弗雷歇距离，它是用来干什么的？

费雷歇distance是求两个序列匹配之后的最大距离，这里需要明确a）两个序列；b）匹配过程；c）最大距离的含义。
a）两个序列的长度可以不同
b）匹配的过程可以是一一对应或者是一对多，这里可以这样理解：（小明拉着他家的狗旺财，在一条笔直的道路上玩耍，假设小明每走一步，旺财也会走一步，这个时候匹配的点就是一一对应的；当小明停下来捡狗屎的时候，如果旺财没有静止的话，旺财走过的所有点与小明当前所在的点就是多对一的关系）
c）最大距离可以理解为上述小明手里狗绳的长度，为什么狗可以走的很远也可以走得很近，因为绳子可能是弹簧绳（笑）。
思考如何实现两个不同长度的序列如何匹配：这里匹配的难点是一对多如何匹配。

1.2 DTW的概念以及算法

引入概念DTW（动态时间规整）这个算法是评估两个序列元素之间的对应关系，根据两个序列元素距离评估两个序列的相似度。这里DTW的作用和弗雷歇距离的是非常相似的，都是评价两个序列之间法的相似程度。
那么DTW是如何进行两个序列的匹配的：这里解释两个匹配中的概念（锁步度量：一对一的匹配；弹性度量：一对多的匹配）。

DTW算法要求：第一个点和第一个点匹配，最后一个点和最后一个点匹配
单向对应，不能回头（就是只能和自己相邻的两个点对应，不能越过已经链接的匹配进行对应）
一一对应，不能为空（这里的一一对应是，每个点都要有对应的点，不是严格意义上的一一对应）
对应之后，距离最近

bilibili关于DWT讲解

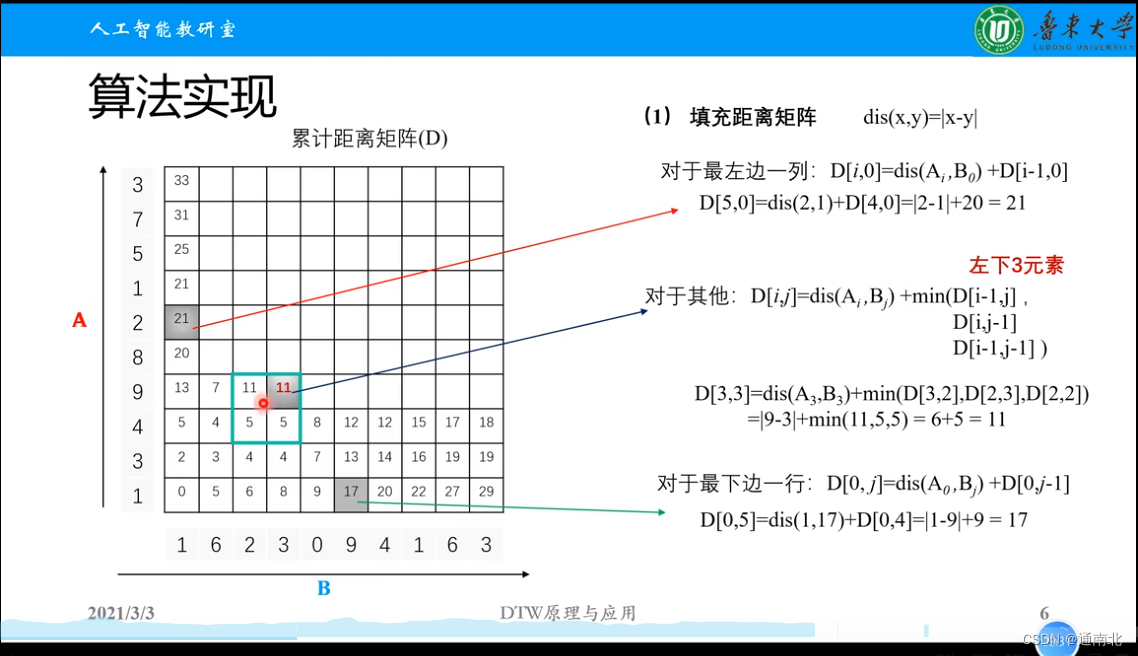
在这里插入图片描述
DTW算法中匹配算法，不需要实现绝对的两个序列的点之间一一对应，这里使用两个序列，一维数点进行举例，如上图所示，1）需要一个计算distance的function这里使用两个点的差的绝对值。2）然后两个序列的点一一对应，计算出每个点的dist然后生成一个m*n的矩阵。3）遍历这个矩阵，获得最小距离的路径path以及最小mean，code如下：

import numpy as np


def euc_dis(a, b):
    return abs(a-b)


def fill_matrix(a: np.array, b: np.array):
    l1 = len(a)
    l2 = len(b)
    dis_all = np.ones((l1, l2)) * -1
    dis_all[0, 0] = euc_dis(a[0], b[0])
    for i in range(1, l1):
        dis_all[i, 0] = euc_dis(a[i], b[0]) + dis_all[i-1, 0]
    for j in range(1, l2):
        dis_all[0, j] = euc_dis(a[0], b[j]) + dis_all[0, j-1]

    for i in range(1, l1):
        for j in range(1, l2):
            if dis_all[i, j] < 0:
                dis_all[i, j] = euc_dis(
                    a[i], b[j]) + min(dis_all[i-1, j], dis_all[i, j-1], dis_all[i-1, j-1])

    return dis_all, l1, l2


def DTW(dis_all: np.ndarray, l1: int, l2: int):
    # 返回匹配的最小距离的集合
    i, j = l1-1, l2-1
    path = []
    res = []
    cnt = 0
    path.append((i, j))
    res.append(dis_all[i, j])
    while True:
        if i > 0 and j > 0:
            m_pre = dis_all[i, j]
            m = min(dis_all[i-1, j], dis_all[i, j-1], dis_all[i-1, j-1])
            if m == dis_all[i-1, j]:
                i = i-1
            elif m == dis_all[i, j-1]:
                j = j-1
            elif m == dis_all[i-1, j-1]:
                j = j-1
                i = i-1
            res.append(m_pre - m)
            path.append((i, j))
            cnt += 1
        elif i == 0 and j == 0:
            path.append((i, j))
            res.append(dis_all[i, j])
            cnt += 1
            break
        elif i == 0:
            path.append((i, j))
            res.append(dis_all[i, j] - dis_all[i, j-1])
            j = j-1
            cnt += 1
        elif j == 0:
            path.append((i, j))
            res.append(dis_all[i, j] - dis_all[i-1, j])
            i = i-1
            cnt += 1

    mean = np.sum(res)/cnt
    print("cnt: ", cnt)
    return mean, res[:-1], path[::-1]


if __name__ == '__main__':
    a = np.array([2, 4, 6, 8])
    b = np.array([2, 3, 4, 6, 5, 7, 8])
    result, l1, l2 = fill_matrix(a, b)
    mean, res, path = DTW(result, l1, l2)
    print("result is:", result)
    print("mean is:", mean)
    print("res is:", res)
    print("path is:", path)

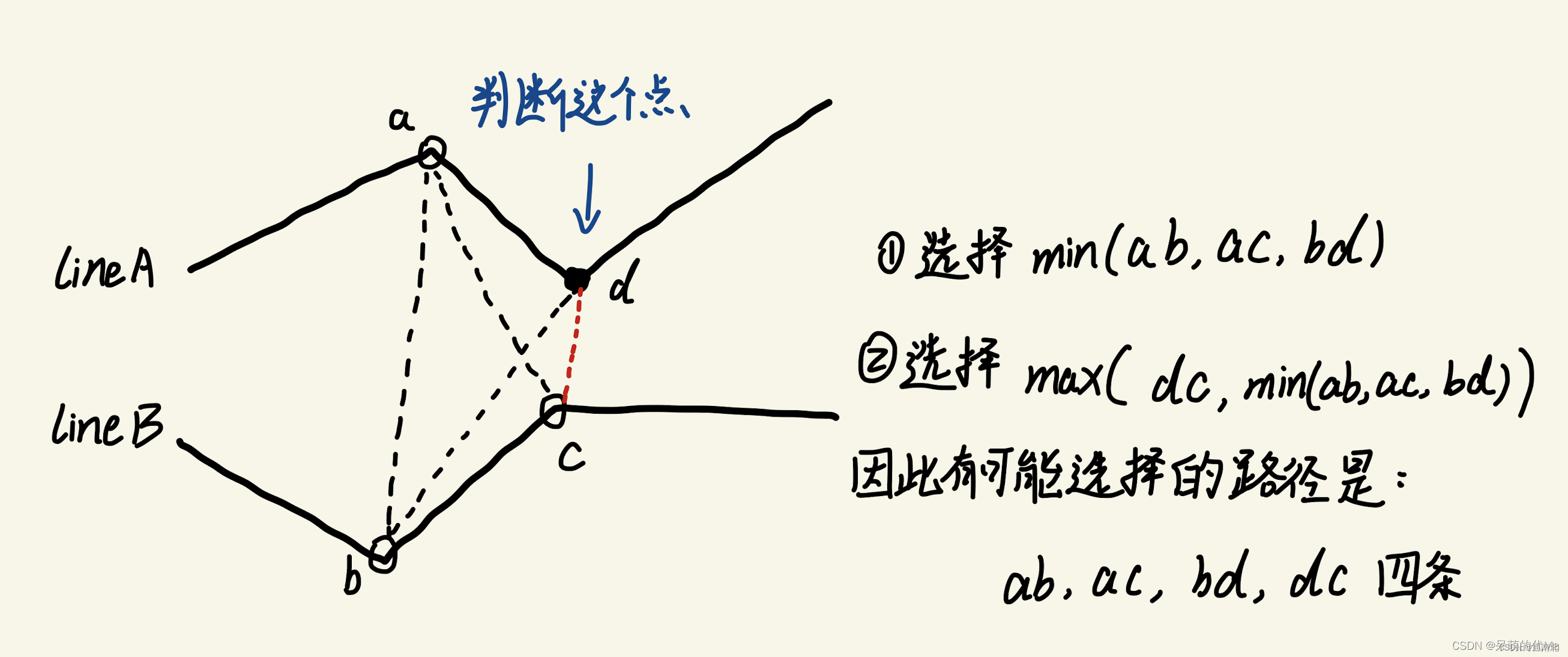
1.3弗雷歇距离的计算

弗雷歇距离也需要计算下方三个连线之间的最小距离
在这里插入图片描述

using namespace std;


class Frechet_dist{
public:
    Frechet_dist(){};
    ~Frechet_dist(){};

    double Frechet_distance(vector<vector<double>> curve_1, vector<vector<double>> curve_2);
    double Euc_dist(vector<double> p1, vector<double> p2);
    double Alignt(int l1, int l2, vector<vector<double>> curve_1, vector<vector<double>> curve_2, Eigen::MatrixXd Dis_all);
    double call_back();


};



#include "frechet_dist.h"
#include <iostream>
#include <math.h>

using namespace std;

double Frechet_dist::Euc_dist(vector<double> p1, vector<double> p2){
    double dis = sqrt(pow((p1[0] - p2[0]), 2) + pow((p1[1] - p2[1]), 2));
    return dis;
}
double min_of_three(double a,double b,double c)
{
    double temp = a;
    if(b < a) temp = b;
    if(temp > c) temp = c;
    return temp;
}
double Frechet_dist::Alignt(int l1, int l2, vector<vector<double>> curve_1, vector<vector<double>> curve_2, Eigen::MatrixXd Dis_all){
    double dis = 0;
    //多次迭代影响计算效率，这部分改成动态规划会不会稍微好一些
    cout <<  "len1" <<l1  << "len2" << l2 <<endl;
    for(int i = 0; i < l1; i++){
        for(int j = 0; j < l2; j++){
            if( i == 0 && j == 0){
                dis = Euc_dist(curve_1[0], curve_2[0]);
                Dis_all(i, j) = dis;
            }else if(i == 0 && j > 0){
                dis = Euc_dist(curve_1[0], curve_2[j]);
                Dis_all(i, j) = max(dis, Alignt(0, j-1, curve_1, curve_2, Dis_all));
            }else if(j == 0 && i > 0){
                dis = Euc_dist(curve_1[i], curve_2[0]);
                Dis_all(i, j) = max(dis ,  Alignt(i-1, 0, curve_1, curve_2, Dis_all));
            }else{
                dis = Euc_dist(curve_1[i], curve_2[j]);
                Dis_all(i, j) = max(dis , min_of_three(Alignt(i-1, j, curve_1, curve_2, Dis_all), Alignt(i-1, j-1, curve_1, curve_2, Dis_all),
                                    Alignt(i, j-1, curve_1, curve_2, Dis_all)));
            }
        }
    }
    cout << Dis_all << endl;
    return Dis_all(l1,l2);
}

double Frechet_dist::Frechet_distance(vector<vector<double>> curve_1, vector<vector<double>> curve_2){
    int l1 = curve_1.size();
    int l2 = curve_2.size();
    Eigen::MatrixXd Dis_all = Eigen::MatrixXd::Zero(l1,l2);

    Alignt(l1, l2, curve_1, curve_2, Dis_all);
    // Dis_all[0, 0] = dis;
    // // 动态规划方程的设计
    // // 第一行的计算方式：
    // for(int i = 1; i < l1; i++){
    //     dis = Euc_dist(curve_1[i], curve_2[0]);
    //     Dis_all[0, i] = dis + Dis_all[0, i-1];
    // }

    // // 第一列的计算
    // for(int j = 1; i < l2; i++){
    //     dis = Euc_dist(curve_1[0], curve_2[i]);
    //     Dis_all[0, i] = dis + Dis_all[i-1, 0];
    // }

    // 其他情况
    return 0.0;

}