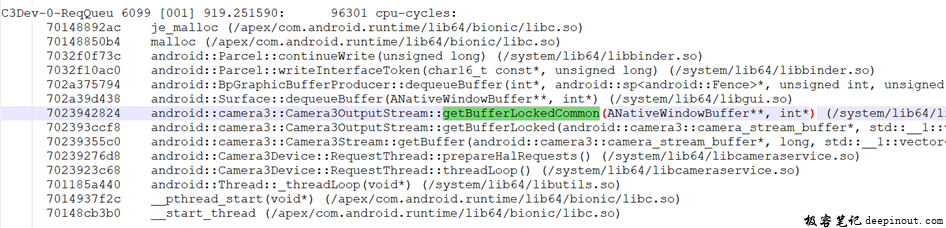
- 为什么使用平方损失而不是绝对差值呢?
答: 二者区别不大,但是绝对差值是一个不可导的函数,在零点的时候,绝对差值的导数会有点难求。
- 损失为什么要求平均?
答:求平均的话,梯度是在一个样本的scale上,不求平均的话,得到的损失是batch_size个样本或者整个样本,那相应的得到梯度会比较大。在损失上除以n其实就等价于梯度也除以了n。学习率就是为了(学习率*梯度)这一块 不要太大也不要太小。除以n的好处就是,不论样本多大或者批量batch_szie多大,梯度的值都是差不多的,因为都是在一个样本的scale上,这样比较好调学习率
- 线性回归损失函数是不是通常都是mse?
答:是的。一般都是。

- 不管是 梯度下降gd 还是随机梯度下降 sgd怎么找到合适的学习率?有什么好的方法吗?
答:一是可以找到一个对学习率不那么敏感的算法,比如说adam。二是可以进行合理的参数初始化使得学习率很容易取得。
- batch_size 是否会最终影响模型结果?
答:batch_size过小会有利于梯度计算的精确。在丢弃法dropout,batch_size在同样的计算,例如扫数据扫多少遍,epoch=3,batch_size越小,对收敛越好。随机梯度下降理论上是带来了噪音(跟真实的数据的差距),采样样本越小,噪音越多。
例如有一百万个样本,每次采样两张图片,那么噪音会比较大,跟真实的方向会差很远。
但是噪音对神经网络是件好事,因为现在深度神经网络都太复杂了,一定的噪音,使得你不会走偏。噪声可以防止过拟合,使得整个模型的泛化性更好。
- 训练过程中,过拟合和欠拟合情况下,学习率和批量大小该如何进行调整呢?有什么常见的策略吗?
答:理论上,学习率和批量大小不太会影响到最后的收敛结果。
- 针对batch_size大小的数据集进行网络训练的时候,网络中每个参数更新时减去的梯度是batch_size中每个样本对应参数梯度求和后取得平均值吗?
答:是的。
- detach()有什么作用?
答:希望将某些计算移动到记录的计算图之外,那就使用detach()。此外,想转numpy,也需要先做一下detach()
- 本质上要用SGD,是因为大部分的实际loss太复杂,推导不出导数为0的解,只能逐个batch去逼近。(只有线性回归有显示解)


![[附源码]计算机毕业设计疫苗药品批量扫码识别追溯系统Springboot程序](https://img-blog.csdnimg.cn/a50133befbc849f58525cdf9da2911fc.png)




![[附源码]计算机毕业设计校园招聘微信小程序Springboot程序](https://img-blog.csdnimg.cn/1bd458124b2d41d693bf86d8f8b94b73.png)