●多项式计算
一维多项式就是包含一个变量的多项式,一个一维多项式示例如下:
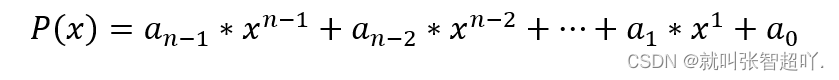 一维多项式求值就是对于上述多项式,计算在指定的x处的函数值。一个通用的计算多项式值的算法可以采用递推的方式,可以将上述多项式变为如下的等价形式(提公因式变形):
一维多项式求值就是对于上述多项式,计算在指定的x处的函数值。一个通用的计算多项式值的算法可以采用递推的方式,可以将上述多项式变为如下的等价形式(提公因式变形):
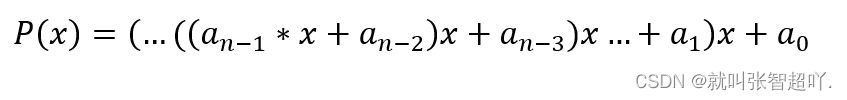 下面,我们按照这个算法来计算我们程序中的多项式。宏定义中已规定多项式系数的个数为7,并且在程序中我们输入系数值,则多项式如下所示:
下面,我们按照这个算法来计算我们程序中的多项式。宏定义中已规定多项式系数的个数为7,并且在程序中我们输入系数值,则多项式如下所示:
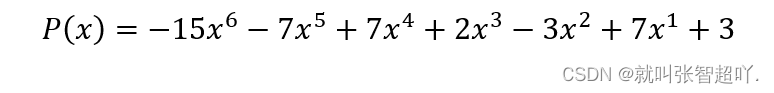 输入的6个未知数x的值分别为,-2、-0.5、1、2、3.7、4 ,带入上式多项式则可知我们要求以下几个多项式的值:
输入的6个未知数x的值分别为,-2、-0.5、1、2、3.7、4 ,带入上式多项式则可知我们要求以下几个多项式的值:
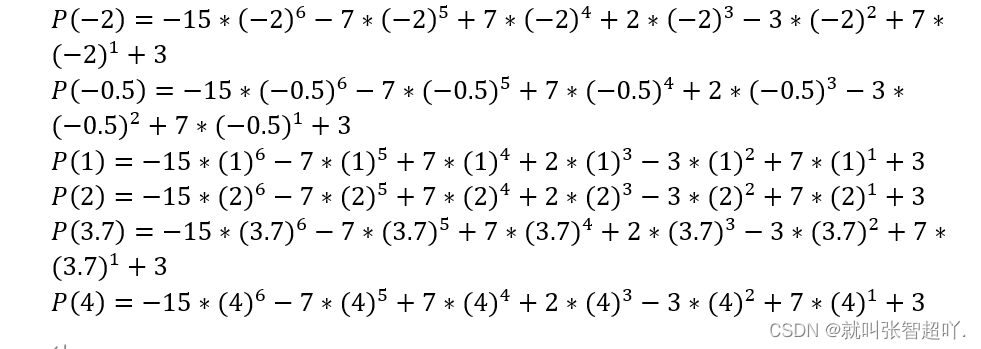 最后在程序中用计算多项式值的算法对其进行计算,并求得结果。
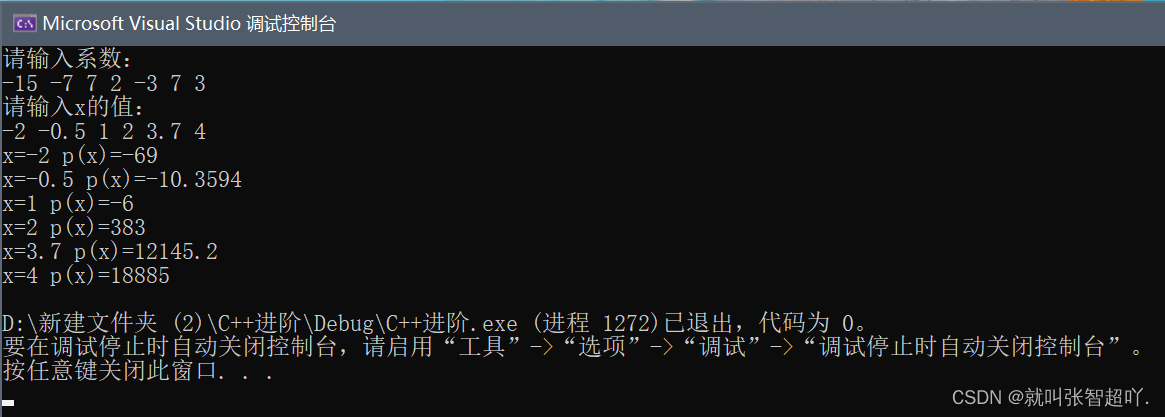
最后在程序中用计算多项式值的算法对其进行计算,并求得结果。
#include<iostream>
using namespace std;
#define sizea 7 //多项式系数个数
#define sizex 6 //未知数x的个数
class calculator {
public:
double polynomials_1(double x)
{
result = a[sizea - 1];
for(int i=sizea-2;i>=0;i--)
{
result = result * x + a[i];
//P(x)=A(n-1)*X^n-1+A(n-2)*X^n-2+...+A(1)*x+A(0)
//P(x)=(...((A(n-1)X+A(n-2))X+A(n-3))X+...+A1)x+A(0)
}
return result;
}
double a[sizea];
double x[sizex];
double result;
};
void polynomials(calculator &c)
{
for (int i = 0; i < sizex; i++)
{
c.polynomials_1(c.x[i]);
cout << "x=" << c.x[i] << " " << "p(x)=" << c.result << endl;
}
}
void text()
{
calculator c;
cout << "请输入系数:" << endl;
for(int i=0;i<sizea;i++)
{
cin >> c.a[i];
}
cout << "请输入x的值:" << endl;
for(int j=0;j<sizex;j++)
{
cin >> c.x[j];
}
polynomials(c);
}
int main()
{
text();
}
●多项式乘法
多项式乘法就是将两个多项式进行相乘,最后得到一个新的多项式。如下所示:
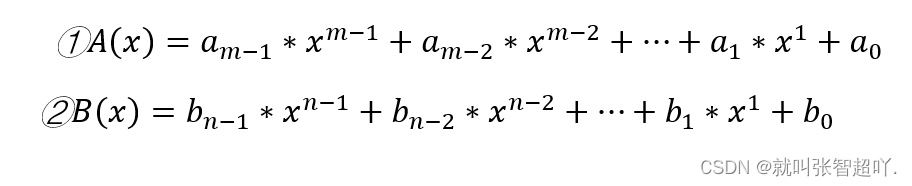 则这两个多项式相乘的结果如下:
则这两个多项式相乘的结果如下:
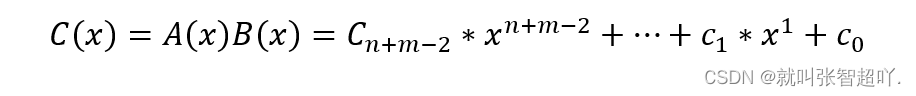
在下面的程序中,宏定义已确定多项式①的系数个数为6个,多项式②的系数个数为4个,则两个多项式如下所示:
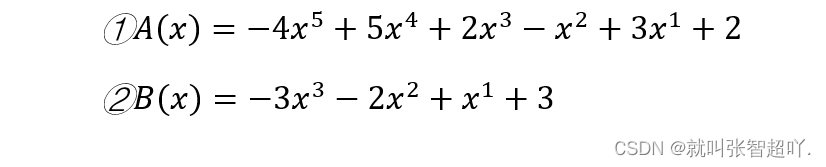
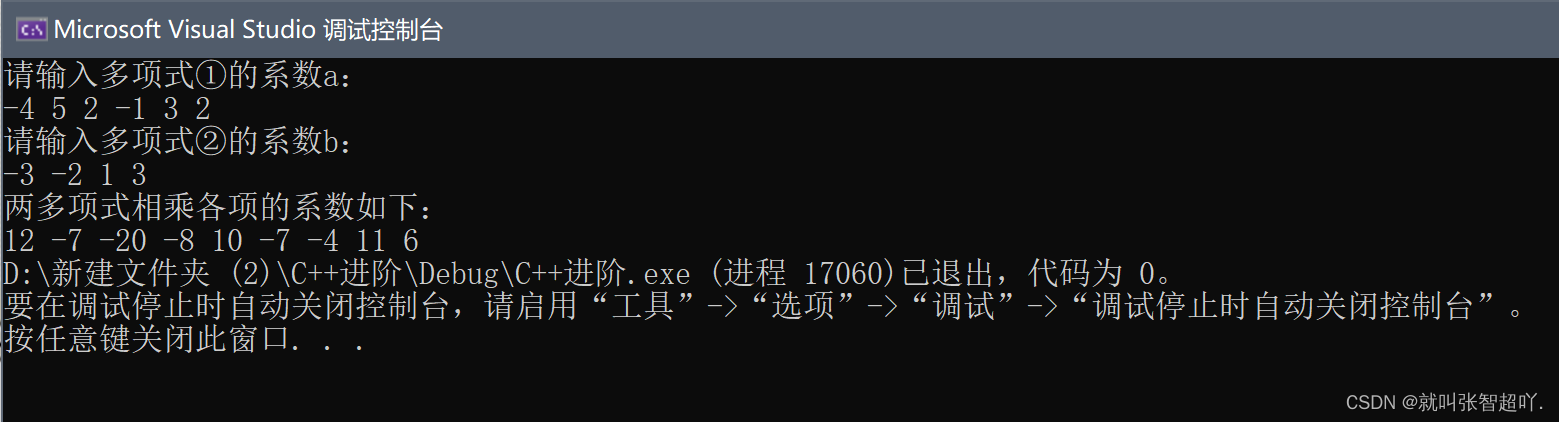
最后在程序中运用两个多项式相乘的算法公式对其进行计算,并且求得结果。
#include<iostream>
using namespace std;
#define sizea 6 //多项式①的系数个数
#define sizeb 4 //多项式②的系数个数
#define sizec 9
class calculator {
public:
void polynomialsmull()
{
for(int i=0;i<sizea;i++)
{
for(int j=0;j<sizeb;j++)
{
c[i + j] += a[i] * b[j];
/*
[0]=[0]*[0]/[1]=[0]*[1]/[2]=[0]*[2]/[3]=[0]*[3]
[1]=[1]*[0]/[2]=[1]*[1]/[3]=[1]*[2]/[4]=[1]*[3]
[2]=[2]*[0]/[3]=[2]*[1]/[4]=[2]*[2]/[5]=[2]*[3]
...
*/
}
}
}
void showresult()
{
cout << "两多项式相乘各项的系数如下:" << endl;
for (int k = 0; k < sizec; k++)
{
cout << c[k] << " ";
}
}
double a[sizea];
double b[sizeb];
double c[sizec] = {0}; //先将该数组每项置为0
};
void text()
{
calculator c;
cout << "请输入多项式①的系数a:" << endl;
for(int i=0;i<sizea;i++)
{
cin >> c.a[i];
}
cout << "请输入多项式②的系数b:" << endl;
for(int j=0;j<sizeb;j++)
{
cin >> c.b[j];
}
c.polynomialsmull();
c.showresult();
}
int main()
{
text();
}
●多项式除法
多项式除法就是将两个多项式进行相除,最后得到一个商多项式和余多项式,如下所示得两个多项式:
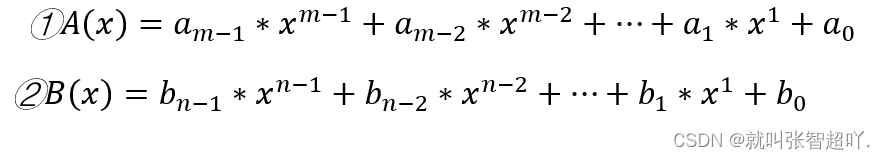
通过推算我们可以知道商多项式为 r(x)的最高次数为k=m-n,余多项式的最高次数为n-2.在数学上通过综合除法来计算商多项式 r(x)和余多项式为 l(x)中的各个系数,结合程序可进行进一步的细致理解。商多项式 l(x)的各个系数由下列递推算法来求得:
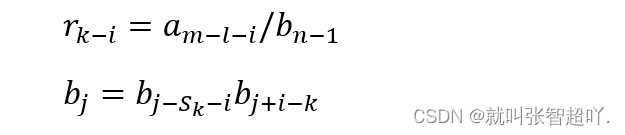 在下面的程序中,宏定义已确定多项式①的系数个数为5个,多项式②的系数个数为3个,则两个多项式如下所示:
在下面的程序中,宏定义已确定多项式①的系数个数为5个,多项式②的系数个数为3个,则两个多项式如下所示:
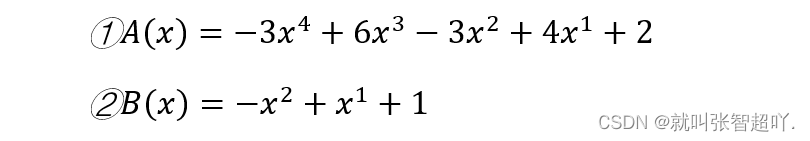
最后在程序中运用两个多项式相除的算法公式及其数学内容对其进行计算,并且求得结果。
#include<iostream>
using namespace std;
#define sizea 5 //多项式①的系数项个数
#define sizeb 3 //多项式②的系数项个数
#define sizer 3
#define sizel 2
class calculator {
public:
void polynomials_div()
{
//计算商多项式系数和余多项式系数
int m, n;
n = sizea - 1;
for(int i=sizer;i>0;i--)
{
r[i - 1] = a[n] / b[sizeb - 1]; //商
m = n;
for (int j = 1; j <= sizeb - 1; j++)
{
a[m - 1] -= r[i - 1] * b[sizeb - j - 1]; //余
m -= 1;
}
n -= 1;
}
for (int k = 0; k < sizel; k++)
{
l[k] = a[k];
}
}
void showresult()
{
cout << "请输出商多项式:" << endl;
for (int i = 0; i < sizer; i++)
{
cout << r[i]<<" ";
}
cout << endl;
cout << "请输出余多项式:" << endl;
for (int i = 0; i < sizel; i++)
{
cout << l[i] <<" ";
}
}
double a[sizea];
double b[sizeb];
double r[sizer] = { 0 };
double l[sizel] = { 0 };
};
void text()
{
calculator c;
cout << "请输入多项式①的系数a:" << endl;
for(int i=0;i<sizea;i++)
{
cin >> c.a[i];
}
cout << "请输入多项式②的系数b:" << endl;
for(int j=0;j<sizeb;j++)
{
cin >> c.b[j];
}
c.polynomials_div();
c.showresult();
}
int main()
{
text();
}

![[附源码]计算机毕业设计疫苗药品批量扫码识别追溯系统Springboot程序](https://img-blog.csdnimg.cn/a50133befbc849f58525cdf9da2911fc.png)




![[附源码]计算机毕业设计校园招聘微信小程序Springboot程序](https://img-blog.csdnimg.cn/1bd458124b2d41d693bf86d8f8b94b73.png)