一、位运算

1.1 思路

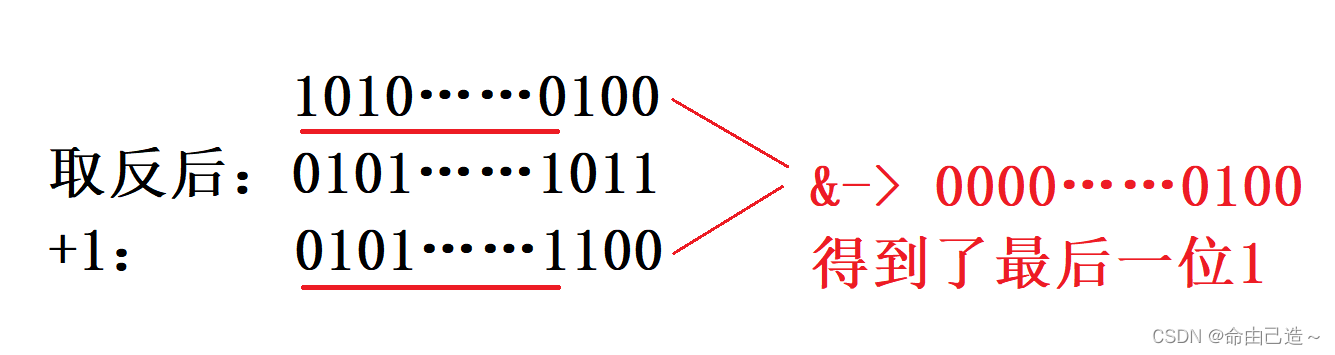
首先知道一个概念：一个正整数的负数等于其按位取反后+1
-x = ~x + 1
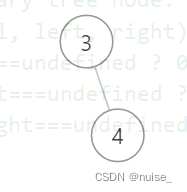
举个例子：3

而我们通过(x & ~x + 1)或(x & -x)就可以得到二进制数最后一位1的大小。
举个例子：

1.1 例题：二进制中1的个数

题目链接

题目描述

给定一个长度为 n 的数列，请你求出数列中每个数的二进制表示中 1 的个数。

输入格式

第一行包含整数 n。
第二行包含 n 个整数，表示整个数列。

输出格式

共一行，包含 n 个整数，其中的第 i 个数表示数列中的第 i 个数的二进制表示中 1 的个数。

数据范围

1≤n≤100000,
0≤数列中元素的值≤109

输入样例：

5
1 2 3 4 5

输出样例：

1 1 2 1 2

#include<iostream>

using namespace std;

int lowbit(int x)
{
    return x & -x;
}

int main()
{
    int n;
    cin >> n;
    while(n--)
    {
        int x;
        cin >> x;
        int sum = 0;
        while(x)
        {
            x -= lowbit(x);
            sum++;
        }
        cout << sum << " ";
    }
    return 0;
}

二、离散化

2.1 概念

联想之前讲过的计数排序八大排序，你都掌握了吗？，当两个坐标差距非常大的时候，就不好处理了。而离散化就是把这些下标全部聚集在一起。直接看例题：

2.2 例题：区间和

题目链接

题目描述

假定有一个无限长的数轴，数轴上每个坐标上的数都是 0。
现在，我们首先进行 n 次操作，每次操作将某一位置 x 上的数加 c。
接下来，进行 m 次询问，每个询问包含两个整数 l 和 r，你需要求出在区间 [l,r] 之间的所有数的和。

输入格式

第一行包含两个整数 n 和 m。
接下来 n 行，每行包含两个整数 x 和 c。
再接下来 m 行，每行包含两个整数 l 和 r。

输出格式

共 m 行，每行输出一个询问中所求的区间内数字和。

数据范围

−109≤x≤109,
1≤n,m≤105,
−109≤l≤r≤109,
−10000≤c≤10000

输入样例：

3 3
1 2
3 6
7 5
1 3
4 6
7 8

输出样例：

8
0
5

思路分析：
下标过于多且可能非常分散，而且是无序且可能重复，那么我们可以把需要用到的下标统计起来，例如（8， 11， 5， 1， 8），然后把他们排序+去重，就得到（1， 5， 8， 11），这样本来需要11个位置存储，现在只需要4个位置就能存住。因为是有序的，所以如果我们要找到下标，就可以用二分查找。
补充一个去重函数：
unique

template <class ForwardIterator>
  ForwardIterator unique (ForwardIterator first, ForwardIterator last);

他会自动去重且把重复的元素排到最后面并且把后边重复下标的第一个位置返回回来。

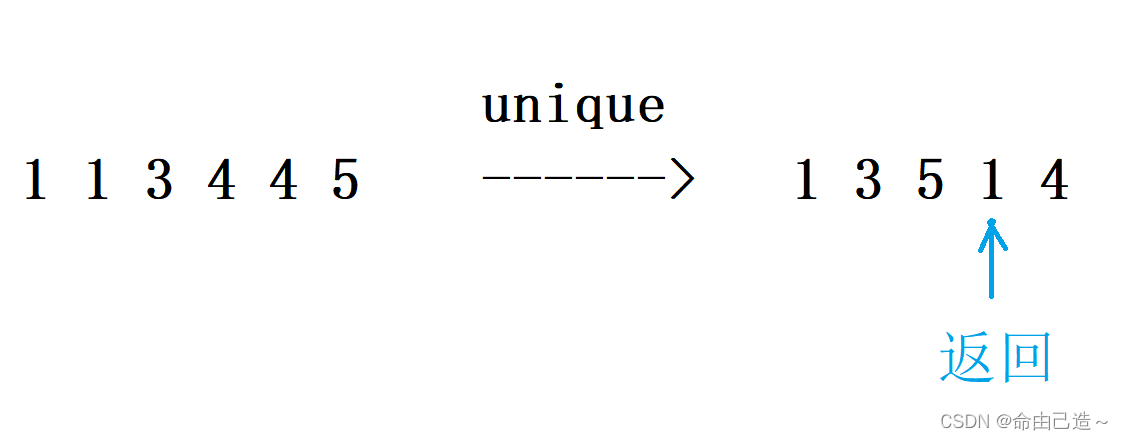
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

const int N = 3e5 + 10;

int a[N], s[N];// a存数据，s存前缀和
vector<int> Index;// 下标
typedef pair<int, int> PII;
vector<PII> add, sum;
// add记录要加的下标及数据
// sum存要加的区间

//通过find找到下标
int find(int x)
{
    int l = 0, r = Index.size() - 1;
    while(l < r)
    {
        int mid = (l + r) >> 1;
        if(Index[mid] >= x)
        {
            r = mid;
        }
        else
        {
            l = mid + 1;
        }
    }
    return r + 1;
}

int main()
{
    int n, m;
    cin >> n >> m;
    for(int i = 0; i < n; i++)
    {
        int x, c;
        scanf("%d %d", &x, &c);
        add.push_back({x, c});
        Index.push_back(x);
    }
    for(int i = 0; i < m; i++)
    {
        int l, r;
        scanf("%d %d", &l, &r);
        sum.push_back({l, r});
        // 需要的下标也要加上
        Index.push_back(l);
        Index.push_back(r);
    }
    // 排序+去重Index
    sort(Index.begin(), Index.end());
    Index.erase(unique(Index.begin(), Index.end()), Index.end());
    for(int i = 0; i < n; i++)
    {
        a[find(add[i].first)] += add[i].second;
    }
    // 求前缀和
    for(int i = 1; i <= Index.size(); i++)
    {
        s[i] = a[i] + s[i - 1];
    }
    for(int i = 0; i < m; i++)
    {
        int l = find(sum[i].first), r = find(sum[i].second);
        printf("%d\n", s[r] - s[l - 1]);
    }
    return 0;
}

三、合并区间

3.1 概念

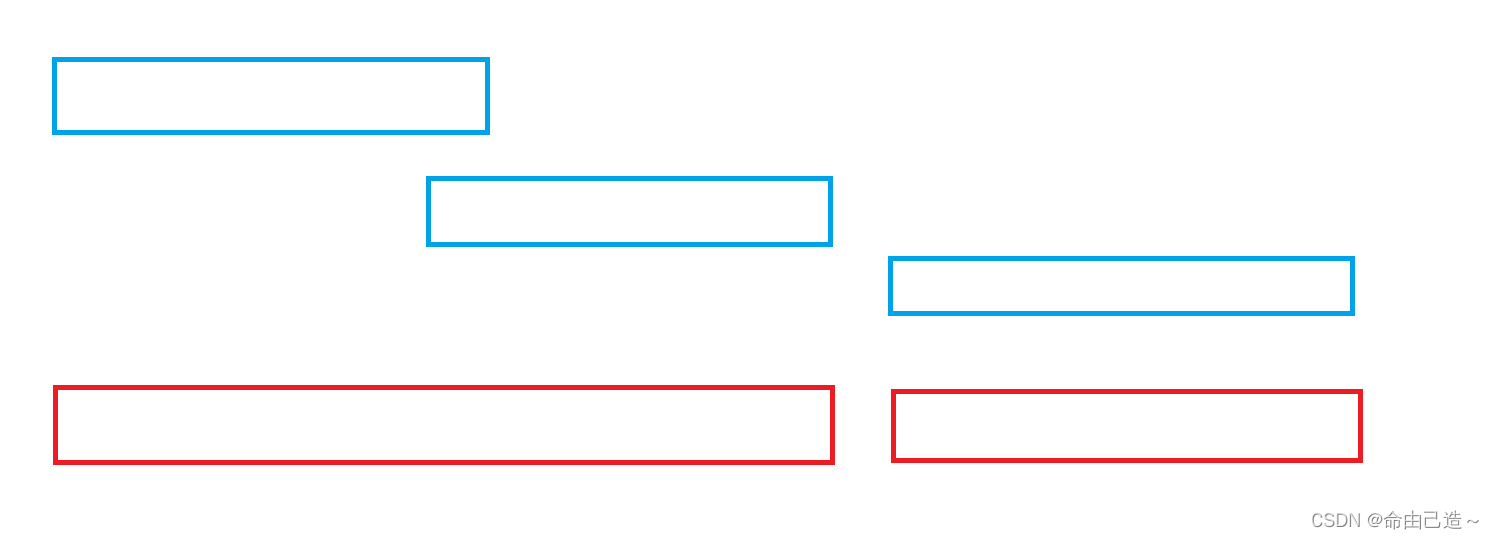
如图，上面三个区间可以合并成两个区间。

3.2 例题：合并区间

题目链接

题目描述

给定 n 个区间 [li,ri]，要求合并所有有交集的区间。
注意如果在端点处相交，也算有交集。
输出合并完成后的区间个数。
例如：[1,3] 和 [2,6] 可以合并为一个区间 [1,6]。

输入格式

第一行包含整数 n。
接下来 n 行，每行包含两个整数 l 和 r。

输出格式

共一行，包含一个整数，表示合并区间完成后的区间个数。

数据范围

1≤n≤100000,
−109≤li≤ri≤109

思路分析
我们先把所有区间存起来，再排序，这样每个区间的起始位置就是有序的。那么两个区间的位置关系只有两种情况：
1️⃣ 左区间的end >= 右区间的start，此时就要合并。
2️⃣ 左区间的end < 右区间的start，此时前面的就为一个空间

那么现在我们就可以设置一个start和end来维护当前区间，当是第一种情况时，调整end，start不变。第二种情况start和end都要去维护下一个区间。
要注意的是最后一个区间我们并没有算上，所以结果要+1

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

typedef pair<int, int> PII;
vector<PII> idx;

int main()
{
    int n;
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        int l, r;
        scanf("%d %d", &l, &r);
        idx.push_back({l, r});
    }
    sort(idx.begin(), idx.end());
    int start = -1e9 - 10, end = -1e9 - 10;
    int sum = 0;
    for(int i = 0; i < idx.size(); i++)
    {
        if(end != -1e9 - 10 && idx[i].first > end)
        {
            ++sum;
            start = idx[i].first;
            end = idx[i].second;
        }
        else
        {
            end = max(end, idx[i].second);
        }
    }
    ++sum;// 加上最后一段区间
    cout << sum << endl;
    return 0;
}