文章目录
- 一:无约束优化问题概述
- 二:线搜索方法
- (1)概述
- (2)线搜索准则
- A:Armijo准则
- ①:概述
- ②:Armjio准则缺陷
- ③:回退法
- ④:代码
- B:Goldstein准则
- ①:概述
- ②:代码
- C:Wolfe准则
- ①:概述
- ②:代码
- D:非单调线搜索准则
- (3)线搜索方法
一:无约束优化问题概述
考虑如下无约束优化问题
m i n x ∈ R n f ( x ) \mathop{min}\limits_{x\in R^{n}}f(x) x∈Rnminf(x)
无约束优化问题是众多优化问题中最基本的一类问题,它对自变量 x x x的取值范围不加限制,所以无需考虑 x x x的可行性
- 对于光滑函数,我们可以较容易地利用梯度和海瑟矩阵的信息来设计算法
- 对于非光滑函数,我们可以利用次梯度来构造迭代格式
无约束优化问题的优化算法主要分为如下两类
-
线搜索类型:根据搜索方向的不同可以分为如下几种,一旦确定了搜索的方向,下一步即沿着该方向寻找下一个迭代点
- 梯度类算法
- 次梯度算法
- 牛顿算法
- 拟牛顿算法
- …
-
信赖域类型:主要针对 f ( x ) f(x) f(x)二阶可微的情形,它是在一个给定的区域内使用二阶模型近似原问题,通过不断直接求解该二阶模型从而找到最优值点
二:线搜索方法
(1)概述
线搜索方法:对于本文最开始的优化问题,采用线搜索方法求解 f ( x ) f(x) f(x)最小值点的过程类似于盲人下山:假设一个人处于某个点 x x x处, f ( x ) f(x) f(x)表示此地的高度,为了寻找最低点,在点 x x x处需要确定如下两件事情
- 下一步应该向哪一个方向行走?
- 沿着该方向行走多远后停下以便选取下一个下山方向
以上这两个因素确定后,便可以一直重复,直到到达 f ( x ) f(x) f(x)的最小值点
线搜索类算法的数学表述为:给定当前迭代点 x k x^{k} xk,首先通过某种算法选取向量 d k d^{k} dk,之后确定正数 α k \alpha_{k} αk,则下一步迭代点可以写作
x k + 1 = x k + α k d k x^{k+1}=x^{k}+\alpha_{k}d^{k} xk+1=xk+αkdk
- d k d^{k} dk:是迭代点 x k x^{k} xk处的搜索方向。此处要求 d k d^{k} dk是一个下降方向,也即 ( d k ) T ∇ f ( x k ) < 0 (d^{k})^{T}\nabla f(x^{k})<0 (dk)T∇f(xk)<0,这个下降性质保证了沿着此方向搜索函数值会减小
- α k \alpha_{k} αk:是相应的步长
所以线搜索类算法的关键是如何选取一个好的方向 d k d^{k} dk和合适的步长 α k \alpha_{k} αk
不同的线搜索算法对于 d k d^{k} dk的选取有着不同的方式,但 α k \alpha_{k} αk的选取方法却基本一致。首先构造辅助函数
ϕ ( α ) = f ( x k + α d k ) \phi(\alpha)=f(x^{k}+\alpha d^{k}) ϕ(α)=f(xk+αdk)
- d k d^{k} dk:是给定的下降方向
- α > 0 \alpha >0 α>0:是该辅助函数的自变量
函数 ϕ ( α ) \phi(\alpha) ϕ(α)的几何意义非常直观:它是目标函数 f ( x ) f(x) f(x)在射线 { x k + α d k : α > 0 } \{x^{k}+\alpha d^{k}:\alpha>0\} {xk+αdk:α>0}上的限制。线搜索的目标时选取合适的 α k \alpha_{k} αk使得 ϕ ( α k ) \phi(\alpha_{k}) ϕ(αk)尽可能小,这要求
- α k \alpha_{k} αk应该使得 f f f充分下降
- 不应该在寻找 α k \alpha_{k} αk上花费过度的计算量
所以一个自然的想法是寻找 α k \alpha_{k} αk使得
α k = a r g m i n α > 0 ϕ ( α ) \alpha_{k}=\mathop{argmin}\limits_{\alpha>0}\phi(\alpha) αk=α>0argminϕ(α)
这种线搜索方法称之为精确线搜索算法,虽然精确线搜索算法可以在多数情况下找到问题的解,但这通常需要非常大的计算量,所以实际应用中很少使用。所以另一个想法是不要求 α k \alpha_{k} αk是 ϕ ( α ) \phi(\alpha) ϕ(α)的最小值点,而仅仅要求 ϕ ( α k ) \phi(\alpha_{k}) ϕ(αk)满足某些不等式性质,因此这类方法称之为非精确线搜索算法,所以我们接下来介绍该类算法的结构
(2)线搜索准则
线搜索准则:在非精确线搜索算法中,选取 α k \alpha_{k} αk需要满足一定的要求,这些要求被称为线搜索准则。不合适的线搜索准则会导致算法无法收敛
- 例如下面这个例子,由于迭代过程中函数值
f
(
x
k
)
f(x^{k})
f(xk)的下降量不够充分,以至于算法无法收敛至极小值点

所以为了避免这种情况发生,必须要引入一些更合理的线搜索准则来确保迭代的收敛性
A:Armijo准则
①:概述
Armijo准则:设 d k d^{k} dk是点 x k x^{k} xk处的下降方向,若
f ( x k + α d k ) ≤ f ( x k ) + c 1 α ∇ f ( x k ) T d k f(x^{k}+\alpha d^{k})\leq f(x^{k})+c_{1}\alpha \nabla f(x^{k})^{T}d^{k} f(xk+αdk)≤f(xk)+c1α∇f(xk)Tdk
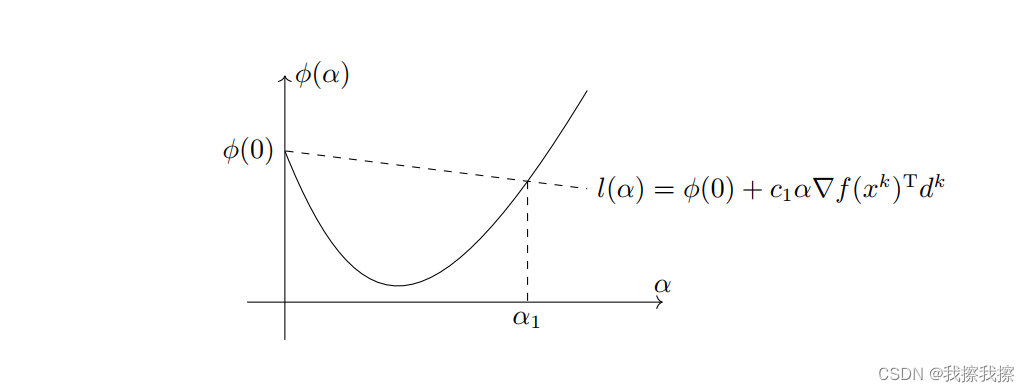
则称步长 α \alpha α满足Armijo准则,其中 c 1 ∈ ( 0 , 1 ) c_{1}\in(0,1) c1∈(0,1)是一个常数。其几何意义是指点 ( α , ϕ ( α ) ) (\alpha, \phi(\alpha)) (α,ϕ(α))必须在直线
l ( α ) = ϕ ( 0 ) + c 1 α ∇ f ( x k ) T d k l(\alpha)=\phi(0)+c_{1}\alpha\nabla f(x^{k})^{T}d^{k} l(α)=ϕ(0)+c1α∇f(xk)Tdk
的下方
如下图所示,区间
[
0
,
α
1
]
[0,\alpha_{1}]
[0,α1]中的点均满足Armijo准则。
d
k
d^{k}
dk为下降方向,这说明
l
(
α
)
l(\alpha)
l(α)方向,这说明
l
(
α
)
l(\alpha)
l(α)斜率为负,选取符合条件的
α
\alpha
α确实会使得函数值下降
②:Armjio准则缺陷
Armjio准则缺陷:实际应用中,参数 c 1 c_{1} c1通常选为一个很小的正数(例如 c 1 = 1 0 − 3 c_{1}=10^{-3} c1=10−3),这使得Armijo准则非常容易得到满足,但仅仅使用Armijo准则无法保证迭代的收敛性。这是因为 α = 0 \alpha=0 α=0时显然满足条件 f ( x k + α d k ) ≤ f ( x k ) + c 1 α ∇ f ( x k ) T d k f(x^{k}+\alpha d^{k})\leq f(x^{k})+c_{1}\alpha \nabla f(x^{k})^{T}d^{k} f(xk+αdk)≤f(xk)+c1α∇f(xk)Tdk,而这意味着迭代序列中的点固定不变,研究这样的步长是没有意义的,为此Armjio准则需要配合其他准则共同使用
③:回退法
回退法:在优化算法的实现中,寻找一个满足Armijo准则的步长是比较容易的,一个最常用的算法是回退法。给定初值 α ︿ \mathop{\alpha}\limits^{︿} α︿,回退法通过不断以指数方式缩小试探步长,找到第一个满足Armjio准则的点。具体来说,回退法选取
α k = γ j 0 α ︿ \alpha_{k}=\gamma^{j_{0}}\mathop{\alpha}\limits^{︿} αk=γj0α︿
其中
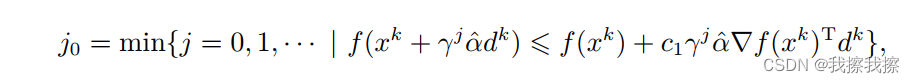
参数 γ ∈ ( 0 , 1 ) \gamma\in(0,1) γ∈(0,1)为一个定的实数,回退法基本过程如下所示

该算法被称为回退法是因为
α
\alpha
α的试验值是由大至小的,它可以确保输出的
α
k
\alpha_{k}
αk能尽量大。此算法也会收敛,因为
d
k
d^{k}
dk是一个下降方向,当
α
\alpha
α充分小时,Armijo准则总是成立的。在实际应用中我们通常也会给
α
\alpha
α设置一个下界,防止步长过小
④:代码
import numpy as np
from sympy import *
# 计算梯度函数
def cal_grad_funciton(function):
res = []
x = []
x.append(Symbol('x1'))
x.append(Symbol('x2'))
for i in range(len(x)):
res.append(diff(function, x[i]))
return res
# 定义目标函数
def function_define():
x = []
x.append(Symbol('x1'))
x.append(Symbol('x2'))
# y = 2 * (x[0] - x[1] ** 2) ** 2 + (1 + x[1]) ** 2
# Rosenbrock函数
y = 100 * (x[1] - x[0] ** 2) ** 2 + (1 - x[0]) ** 2
return y
# 计算函数返回值
def cal_function_ret(function, x):
res = function.subs([('x1', x[0]), ('x2', x[1])])
return res
# 计算梯度
def cal_grad_ret(grad_function, x):
res = []
for i in range(len(x)):
res.append(grad_function[i].subs([('x1', x[0]), ('x2', x[1])]))
return res
# armijo准则
"""
Parameter:
function:函数
grad_function:梯度函数
x:初始迭代点
d:下降方向
c:armijo准的参数,范围为[0-1]
Return:
alpha:步长
"""
def armijo(function, grad_function, x, d, c = 0.3):
# 指定初始步长
alpha = 1.0
# 回退参数
gamma = 0.333
# 迭代次数
k = 1.0
# fd 表示 f(x + alpha * d)
fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d)))
# fk 表示 f(x) + c * alpha * gradf(x) * d
fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
while fd > fk :
fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d)))
fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
alpha *= gamma
k += 1.0
print("迭代次数:", k)
return alpha
# armijo-goldstein准则
if __name__ == '__main__':
function = function_define()
grad_function = cal_grad_funciton(function)
print("函数为:", function)
print("梯度函数为:", grad_function)
x0 = [-10, 10]
d = cal_grad_ret(grad_function, x0)
d = np.dot(-1, d).tolist()
alpha = armijo(function, grad_function, x0, d)
xk = np.add(x0, np.dot(alpha, d))
f = cal_function_ret(function, xk)
print("初始迭代点:", x0)
print("搜索方向为:", d)
print("获取步长为:", alpha)
print("下降点为:", xk)
print("下降点函数值为:", f)

B:Goldstein准则
①:概述
Goldstein准则:为了克服Armijo准则的缺陷,我们需要引入其他准则来保证每一步的 α k \alpha^{k} αk不会太小。既然Armijo准则只要求点 ( α , ϕ ( α ) ) (\alpha, \phi(\alpha)) (α,ϕ(α))必须在某直线下方,那么我们也可以使用相同的形式使得该点必须处在另一条直线的上方,这便是Armijo-Goldstein准则,简称Goldstein准则。设 d k d^{k} dk是点 x k x^{k} xk处的下降方向,若
- f ( x k + α d k ) ≤ f ( x k ) + c α ∇ f ( x k ) T d k f(x^{k}+\alpha d^{k})\leq f(x^{k})+c\alpha \nabla f(x^{k})^{T}d^{k} f(xk+αdk)≤f(xk)+cα∇f(xk)Tdk
- f ( x k + α d k ) ≥ f ( x k ) + ( 1 − c ) α ∇ f ( x k ) T d k f(x^{k}+\alpha d^{k})\geq f(x^{k})+(1-c)\alpha \nabla f(x^{k})^{T}d^{k} f(xk+αdk)≥f(xk)+(1−c)α∇f(xk)Tdk
则称步长 α \alpha α满足Goldstein准则,其中 c ∈ ( 0 , 1 2 ) c\in (0,\frac{1}{2}) c∈(0,21)
同样,Goldstein准则也有非常直观的几何意义,它指的是点 ( α , ϕ ( α ) ) (\alpha, \phi(\alpha)) (α,ϕ(α))必须在以下两条直线之间
- l 1 ( α ) = ϕ ( 0 ) + c α ∇ f ( x k ) T d k l_{1}(\alpha)=\phi(0)+c\alpha\nabla f(x^{k})^{T}d^{k} l1(α)=ϕ(0)+cα∇f(xk)Tdk
- l 2 ( α ) = ϕ ( 0 ) + ( 1 − c ) α ∇ f ( x k ) T d k l_{2}(\alpha)=\phi(0)+(1-c)\alpha\nabla f(x^{k})^{T}d^{k} l2(α)=ϕ(0)+(1−c)α∇f(xk)Tdk
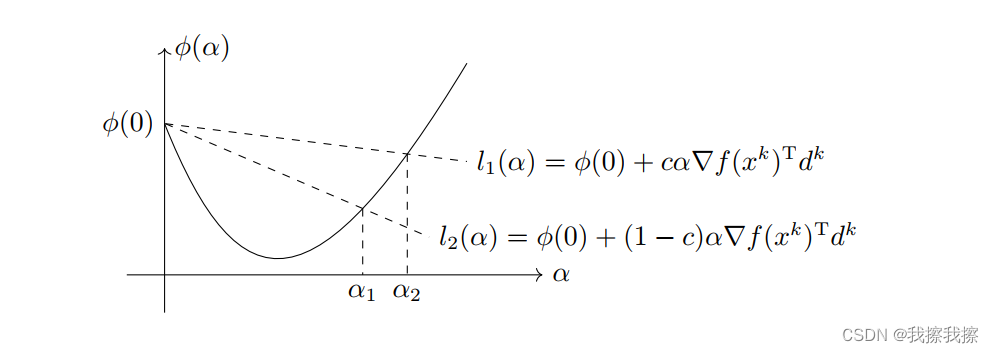
②:代码
import numpy as np
from sympy import *
# 计算梯度函数
def cal_grad_funciton(function):
res = []
x = []
x.append(Symbol('x1'))
x.append(Symbol('x2'))
for i in range(len(x)):
res.append(diff(function, x[i]))
return res
# 定义目标函数
def function_define():
x = []
x.append(Symbol('x1'))
x.append(Symbol('x2'))
# y = 2 * (x[0] - x[1] ** 2) ** 2 + (1 + x[1]) ** 2
# Rosenbrock函数
y = 100 * (x[1] - x[0] ** 2) ** 2 + (1 - x[0]) ** 2
return y
# 计算函数返回值
def cal_function_ret(function, x):
res = function.subs([('x1', x[0]), ('x2', x[1])])
return res
# 计算梯度
def cal_grad_ret(grad_function, x):
res = []
for i in range(len(x)):
res.append(grad_function[i].subs([('x1', x[0]), ('x2', x[1])]))
return res
# armijo-goldstein准则
def armijo_goldstein(function, grad_function, x0, d, c = 0.3):
# 指定初始步长
alpha = 1.0
# 回退参数
gamma = 0.333
# 迭代次数
k = 1.0
# fd 表示 f(x + alpha * d)
fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d)))
# fk 表示 f(x) + c * alpha * gradf(x) * d
fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
# fp 表示 f(x) + (1-c) * alpha * gradf(x) * d
fp = cal_function_ret(function, x0) + (1-c) * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
while fd > fk or fd < fp:
alpha *= gamma
fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d)))
fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
fp = cal_function_ret(function, x0) + (1-c) * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
k += 1.0
print("迭代次数:", k)
return alpha
if __name__ == '__main__':
function = function_define()
grad_function = cal_grad_funciton(function)
print("函数为:", function)
print("梯度函数为:", grad_function)
x0 = [-10, 10]
d = cal_grad_ret(grad_function, x0)
d = np.dot(-1, d).tolist()
alpha = armijo_goldstein(function, grad_function, x0, d)
xk = np.add(x0, np.dot(alpha, d))
f = cal_function_ret(function, xk)
print("初始迭代点:", x0)
print("搜索方向为:", d)
print("获取步长为:", alpha)
print("下降点为:", xk)
print("下降点函数值为:", f)

C:Wolfe准则
①:概述
Wolfe准则:Goldstein准则能够使得函数值充分下降,但是它可能避开了最优函数值
- 如下图所示,一维函数 ϕ ( α ) \phi(\alpha) ϕ(α)的最小值点并不在满足Goldstein准则的区间 [ α 1 , α 2 ] [\alpha_{1}, \alpha_{2}] [α1,α2]中
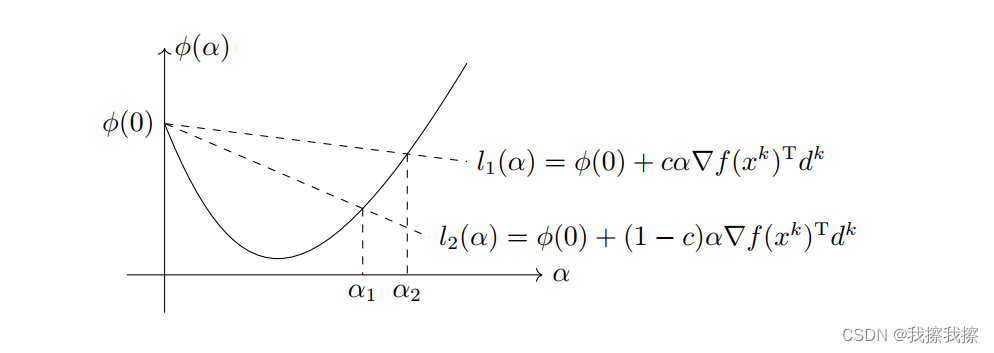
为此,我们引入Armijo准则-Wolfe准则,简称Wolfe准则。设 d k d^{k} dk是点 x k x^{k} xk处的下降方向,若
- f ( x k + α d k ) ≤ f ( x k ) + c 1 α ∇ f ( x k ) T d k f(x^{k}+\alpha d^{k})\leq f(x^{k})+c_{1}\alpha \nabla f(x^{k})^{T}d^{k} f(xk+αdk)≤f(xk)+c1α∇f(xk)Tdk
- ∇ f ( x k + α d k ) T d k ≥ c 2 ∇ f ( x k ) T d k \nabla f(x^{k}+\alpha d^{k})^{T}d^{k} \geq c_{2}\nabla f(x^{k})^{T}d^{k} ∇f(xk+αdk)Tdk≥c2∇f(xk)Tdk(Wolfe准则本质要求)
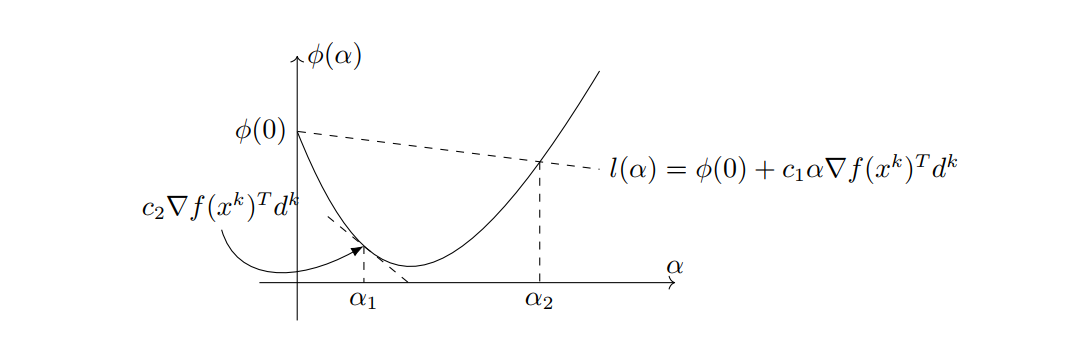
∇ f ( x k + α d k ) T d k \nabla f(x^{k}+\alpha d^{k})^{T}d^{k} ∇f(xk+αdk)Tdk恰好就是 ϕ ( α ) \phi(\alpha) ϕ(α)的导数,所以Wolfe助阵实则要求 ϕ ( α ) \phi(\alpha) ϕ(α)在点 α \alpha α处的切线斜率不能小于 ϕ ‘ ( 0 ) \phi^{`}(0) ϕ‘(0)的 c 2 c_{2} c2倍,如下图所示,区间 [ α 1 , α 2 ] [\alpha_{1}, \alpha_{2}] [α1,α2]中的点均满足Wolfe准则,在实际应用中参数 c 2 c_{2} c2一般取为0.9
②:代码
import numpy as np
from sympy import *
# 计算梯度函数
def cal_grad_funciton(function):
res = []
x = []
x.append(Symbol('x1'))
x.append(Symbol('x2'))
for i in range(len(x)):
res.append(diff(function, x[i]))
return res
# 定义目标函数
def function_define():
x = []
x.append(Symbol('x1'))
x.append(Symbol('x2'))
# y = 2 * (x[0] - x[1] ** 2) ** 2 + (1 + x[1]) ** 2
# Rosenbrock函数
y = 100 * (x[1] - x[0] ** 2) ** 2 + (1 - x[0]) ** 2
return y
# 计算函数返回值
def cal_function_ret(function, x):
res = function.subs([('x1', x[0]), ('x2', x[1])])
return res
# 计算梯度
def cal_grad_ret(grad_function, x):
res = []
for i in range(len(x)):
res.append(grad_function[i].subs([('x1', x[0]), ('x2', x[1])]))
return res
# armijo-wolfe准则
def armijo_wlofe(function, grad_function, x0, d, c = 0.3):
# wolfe准则参数
c2 = 0.9
# 指定初始步长
alpha = 1.0
# 二分法确定alpah
a, b = 0, np.inf
# 迭代次数
k = 1.0
# gk表示gradf(x)
gk = cal_grad_ret(grad_function, x0)
# fd 表示 f(x + alpha * d)
fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d)))
# fk 表示 f(x) + c * alpha * gradf(x) * d
fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
# gp表示gradf(x + alpha * d)
gp = cal_grad_ret(grad_function, np.add(x0, np.dot(alpha, d)))
while True:
if fd > fk:
b = alpha
alpha = (a + b) / 2
fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d)))
fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
gp = cal_grad_ret(grad_function, np.add(x0, np.dot(alpha, d)))
k = k + 1
continue
if np.dot(gp, d) < c2 * np.dot(gk, d):
a = alpha
alpha = np.min(2 * alpha, (a + b) / 2)
fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d)))
fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
gp = cal_grad_ret(grad_function, np.add(x0, np.dot(alpha, d)))
k = k + 1
continue
break
print("迭代次数:", k)
return alpha
if __name__ == '__main__':
function = function_define()
grad_function = cal_grad_funciton(function)
print("函数为:", function)
print("梯度函数为:", grad_function)
x0 = [-10, 10]
d = cal_grad_ret(grad_function, x0)
d = np.dot(-1, d).tolist()
# alpha = armijo(function, grad_function, x0, d)
alpha = armijo_wlofe(function, grad_function, x0, d)
xk = np.add(x0, np.dot(alpha, d))
f = cal_function_ret(function, xk)
print("初始迭代点:", x0)
print("搜索方向为:", d)
print("获取步长为:", alpha)
print("下降点为:", xk)
print("下降点函数值为:", f)

D:非单调线搜索准则
以上三种准则都有一个共同点:使用这些准则产生的迭代点序列都是单调的,但在实际应用中,非单调算法有时会有更好的效果,这里主要介绍两种
Grippo准则:设 d k d^{k} dk是点 x k x^{k} xk处的下降方向, M > 0 M>0 M>0为给定的正整数,以下不等式可以作为一种线搜索准则
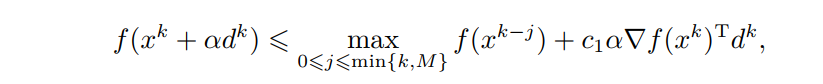
其中 c 1 ∈ ( 0 , 1 ) c_{1}\in (0,1) c1∈(0,1)为给定的常数。该准则和Armijo准非常相似,区别在于Armijo准则要求下一次迭代的函数值 f ( x k + 1 ) f(x^{k+1}) f(xk+1)相对于本次迭代的函数值 f ( x k ) f(x^{k}) f(xk)有充分的下降,而上述准则只需要下一步函数值相比前面至多 M M M步以内迭代的函数值有下降就可以了,显然该准则的要求要比Armijo准则更宽,它也不要求 f ( x k ) f(x^{k}) f(xk)的单调性
Zhang,Hager准则:设 d k d^{k} dk是点 x k x^{k} xk处的下降方向, M > 0 M>0 M>0为给定的正整数,以下不等式可以作为一种线搜索准则
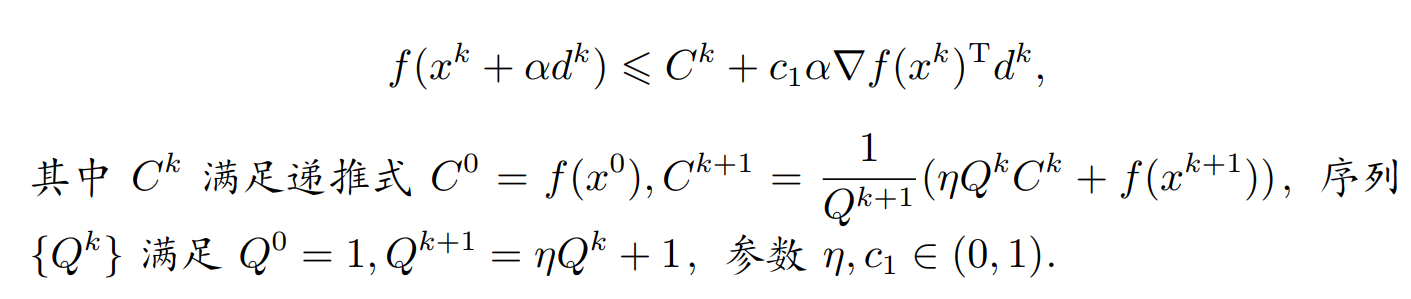
我们可以用以下的方式理解此准则:
- 变量 C k C^{k} Ck实际上是本次搜索准则的参照函数值,也即充分下降性质的起始标准
- 而下一步的标准 C k + 1 C^{k+1} Ck+1则是函数值 f ( x k + 1 ) f(x^{k+1}) f(xk+1)和 C k C^{k} Ck的凸组合,并非仅仅依赖于 f ( x k + 1 ) f(x^{k+1}) f(xk+1),而凸组合的两个系数由参数 η \eta η决定。可以看到,当 η = 0 \eta=0 η=0时,此准则就是Armijo准则




![[附源码]计算机毕业设计校园招聘微信小程序Springboot程序](https://img-blog.csdnimg.cn/1bd458124b2d41d693bf86d8f8b94b73.png)




![深度强化学习的组合优化[1] 综述阅读笔记](https://img-blog.csdnimg.cn/57d57efb3a1f429db78d1be169df3ee3.png)