题目描述:

题目解读:
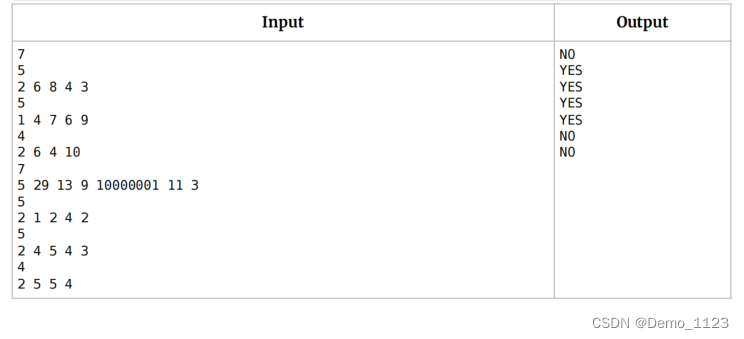
给定数组a[n],ai>0,问能否得到一个数组b[n],数组b中的元素都大于0且全奇or全偶。
数组b中的元素bi=ai or ai-aj(1<j<n)。
解题思路:
数组b中的元素都大于0且全奇or全偶。分析所有情况:
如果a[n]全为偶或全为奇,则b[n]全偶或全奇,必然满足要求;
如果a[n]奇偶都有,想实现b[n]全偶或全奇,必然需要使用bi=ai-aj运算,
对于减法: 奇-偶=奇;奇-奇=偶;偶-偶=偶;偶-奇=奇;
对于值比较大的元素,可以自由选择减去奇数还是偶数(而且减去后还大于0),来实现最终的全奇全偶;唯一需要重点考虑的是最小元素的奇偶性,因为题目要求每个元素需要大于0,故最小元素无法通过减法运算改变奇偶性。
如果最小值是奇数,那其他偶数-奇数,都可变为奇数,即使是最小偶数也可以减最小奇数来变为奇数,故可以满足要求;
如果最小值为偶数,其他奇数-偶数,还是奇数,无法变偶;奇数-奇数可以变偶数,但是最小奇数没有奇数给它减,所以无法满足要求。
综上所述,返回NO的唯一条件是,数组元素奇偶都有,且最小值为偶数。
代码实现:
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#define MAX 200000 //注意题目中要求的变量取值范围
#include<iostream>
using namespace std;
void Solve() {
int n,i=0;
int num[MAX];
int flgodd = 0,flgeven=0;
int minnum = 1e9;
scanf("%d", &n);
for (i = 0; i < n; i++) {
scanf("%d", &num[i]);
if (num[i] % 2 == 1) { //奇数
flgodd = 1;
minnum = min(num[i], minnum);
}
else { //偶数
flgeven = 1;
minnum = min(num[i], minnum);
}
}
if (flgodd == 1&& flgeven == 1) {
if (minnum % 2 == 0) {
printf("NO\n");
}else printf("YES\n");
}
else printf("YES\n");
return;
}
int main() {
int t;
scanf("%d", &t);
while (t--) Solve();
return 0;
}遇到的错误:全奇全偶的判断使用两个flg标记来实现,应该有更简单的办法。


![[Nacos] Nacos Server处理心跳请求 (八)](https://img-blog.csdnimg.cn/b40e497e471c4e099cdce5071b100315.png)