目录
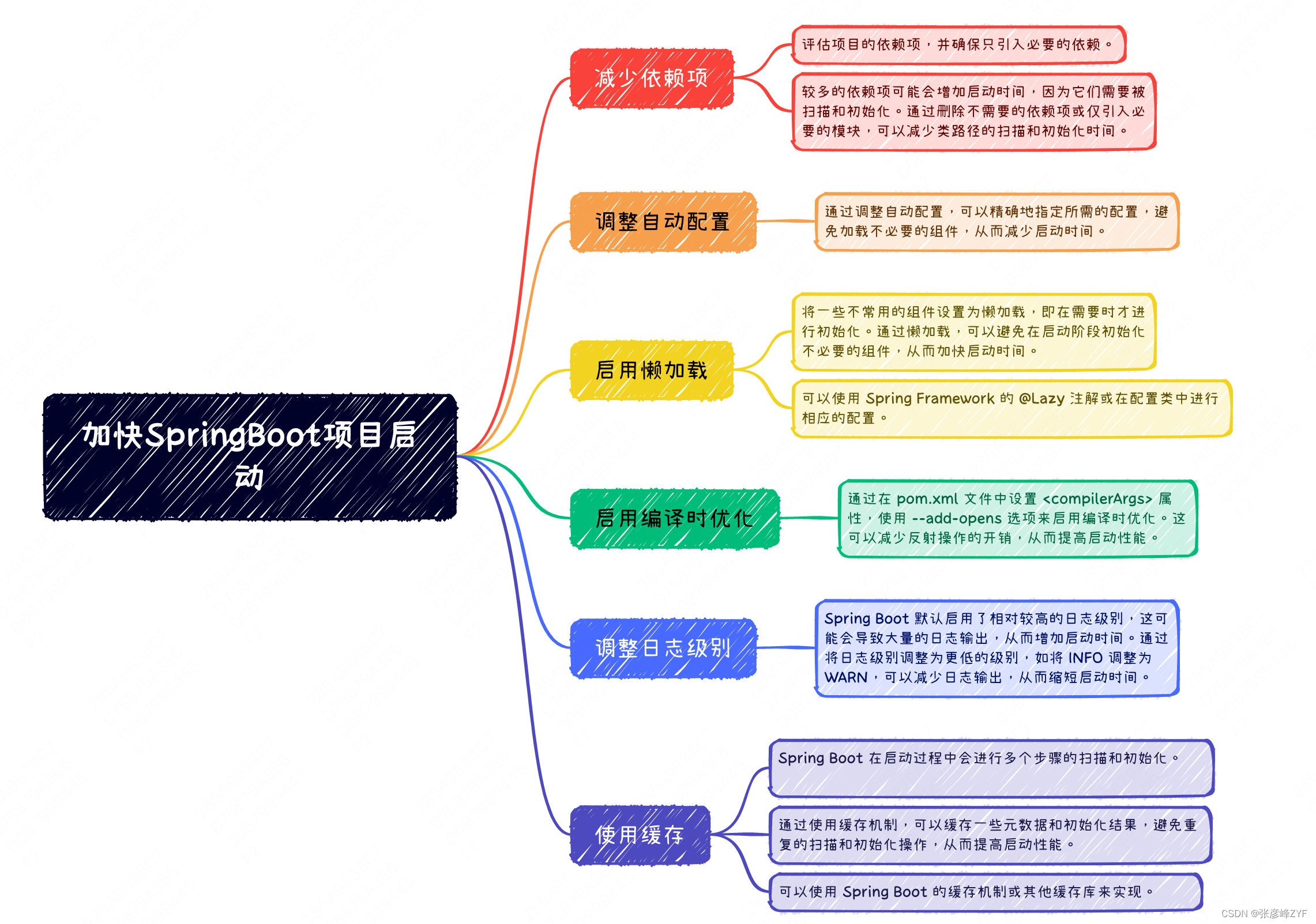
初步认识
逆元
定义
应用
费马小定理
好久没有更新我们的数论专题板块了,今天,我们就来探究一下新知——逆元。
初步认识
在数据非常大的情景下,我们通常会对数据先进行取模运算,来计算在一定的范围内进行处理。而运算的过程中,针对(a+b)%p,(a-b)%p和(a*b)%p,我们都可以通过运用分配律将数据缩小在一个在合理的范围内,再进行精确计算。即有(a+b)%p = (a%p+b%p)%p、(a-b)%p=(a%p-b%p)%p和(a*b)%p=(a%p*b%p)%p。
如果当a和b很大时,我们可以先取模将数据降区间后再进一步计算。但是对于(a/b)%p,它是不满足分配律的,那怎么办呢?对于一些数据,我们必须在中间过程先对其进行求余后再运算,否则数据将会太大,在计算机中进行除法运算的时候可能会损失精度,导致答案变小,那怎么才能解决这个问题呢?
我们就下来讲的逆元就能帮您初步解决这个疑难困惑。
逆元
在中,四则运算都要在模n的意义下,如Z12中,9+3=0,2*6=0。因此,在模运算中,我们知道,减法可以通过补数转化为加法,如在时钟系统中,(8-2)12 = 6,模12的系统中,2的补数是10,因此8-2可以转化为加法运算:(8+10)12 = (8+4+6)12 = (12+6)12 = 6(注,最终的结果不能超过12,即都要模12,相当于以12为周期)。同样,除数如果存在逆元的话,除法也可以转化为乘法,即除以一个数等于乘上这个数的逆元。如在模取9的系统中,(7÷2)9 = (7×5)9。那么,什么是逆元呢?
定义
如果一个线性同余方程,那么我们就称x为a mod b的逆元,记作
.
应用
换一种表述方式:在模n的意义下的两元素a和b(指以n为模的系统里,如时钟的计量范围是0~11,时钟就是以12位模的系统),满足
,比如在模为9的系统中,
,那么我们就说a、b互为模n意义下乘法的逆元,记做
,
。如2和5互为模9意义下乘法的逆元,记做
。
那么开始的例子中7÷2在模9的系统中是什么意思呢?我们知道剩余系中的每一个元素都对应一个同余等价类,所以7÷2的实际含义是:假定有两个整数a、b,满足a/b是整数),且a和b除以9的余数分别是7和2,那么a/b除以9的余数等于(7÷2)9= (16÷2)9=8%9=8。而(7×5)9=8。即(7÷2)9 = (7×5)9=8。
当a、m互素时,若ax≡1(mod m),则称x是a关于模m的逆元,记做。且在[0,m]范围内,a的逆元是唯一的。
证明(反证法证明唯一性:
若a有两个逆元0<x1<x2<m,即:ax1≡ax2≡1(mod m)。那么显然有m|a(x2-x1)成立,又gcd(a,m)=1。因此m|(x2-x1),即0<m<x2-x1。与0<x1<x2<m矛盾。故假设不成立。
又在概述中可以发现将一个整数乘以a^(-1)等价于这个整数除以a,即在模意义下将除法转化为了乘法。即:(注:这里
是在模m的系统下的)。那么,问题又来了,如何求逆元呢?我们需要先了解以下几个概念!
费马小定理
费马大定理众所周知,我们现在来看看费马小定理
若p为素数,且a和p互素,则有。
证明:∵p为素数,且a和p互素
∴a从1到(p-1)的倍数,即a,2a,3a,...,(p-1)a中没有一个是p的倍数,而且任意两个数模p都不同余。
∴a,2a,3a,...,(p-1)a这(p-1)个数对模p的同余是1,2,...,(p-1)的排列。
∴。即
。即
得证。易得,对于任意整数a,若p为素数,则有
。
费马小定理的应用就是转化,当p为素数,a和p互素时,则:
今天的文章就讲这么多了,下一篇博客我会继续讲如何推出逆元以及讲解欧拉定理。再见!!

![[Nacos] Nacos Server处理心跳请求 (八)](https://img-blog.csdnimg.cn/b40e497e471c4e099cdce5071b100315.png)