✨博主:命运之光
✨专栏:算法基础学习

目录
✨堆
🍓堆模板:
✨哈希表
🍓一般哈希模板:
🍓字符串哈希模板:
前言:算法学习笔记记录日常分享,需要的看哈O(∩_∩)O,感谢大家的支持!
✨堆
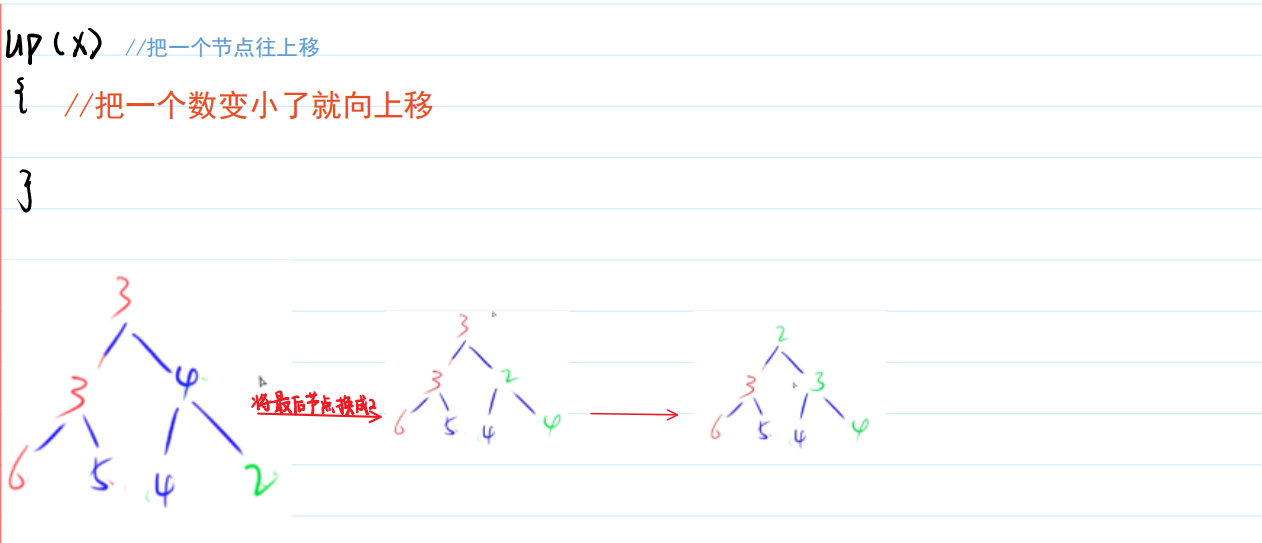
如何手写一个堆?
1.插入一个数 heap[++size]=x;up(size);
2.求集合当中的最小值 heap[1]
3.删除最小值//用最后一个元素覆盖掉第一个元素heap[1]=heap[size];size--;down(1);
4.删除任意一个元素 heap[k]=heap[size];size--;down(k);up(k);
5.修改任意一个元素 heap[k]=x;down(k);up(k);
堆的基本结构:完全二叉树//除最后一层节点之外,上面所有结点都是满的,最后一层结点从左到右排列

堆的存储:用一维数组存

堆可以使用一维数组来进行存储。一维数组可以使用连续的内存空间来表示堆的结构。
堆是一种完全二叉树,可以按照从上到下、从左到右的顺序将其节点依次存储在一维数组中。对于一个具有 n 个节点的堆,可以使用一个长度为 n 的一维数组来存储。
假设堆的根节点存储在数组的索引为 0 的位置。对于任意一个节点 i,其左子节点的索引为 2i+1,右子节点的索引为 2i+2。同时,对于一个节点 i 的父节点,其索引为 (i-1)/2。
这种数组表示的好处是可以通过索引计算节点之间的关系,不需要使用指针或引用。
以下是一个示例,展示如何使用一维数组存储堆:
class Heap:
def __init__(self):
self.heap = []
def parent(self, i):
return (i - 1) // 2
def left_child(self, i):
return 2 * i + 1
def right_child(self, i):
return 2 * i + 2
def insert(self, item):
self.heap.append(item)
self.heapify_up(len(self.heap) - 1)
def heapify_up(self, i):
while i != 0 and self.heap[i] < self.heap[self.parent(i)]:
self.heap[i], self.heap[self.parent(i)] = self.heap[self.parent(i)], self.heap[i]
i = self.parent(i)
def extract_min(self):
if len(self.heap) == 0:
return None
root = self.heap[0]
self.heap[0] = self.heap[-1]
self.heap.pop()
self.heapify_down(0)
return root
def heapify_down(self, i):
while (left := self.left_child(i)) < len(self.heap):
smallest = left
right = self.right_child(i)
if right < len(self.heap) and self.heap[right] < self.heap[left]:
smallest = right
if self.heap[i] <= self.heap[smallest]:
break
self.heap[i], self.heap[smallest] = self.heap[smallest], self.heap[i]
i = smallest上述示例代码展示了一个最小堆的实现。堆的插入操作使用了堆化上移(`heapify_up`),从插入位置开始,将节点与其父节点进行比较并交换,直到满足堆的性质为止。堆的删除操作使用了堆化下移(`heapify_down`),从根节点开始,将节点与其较小的子节点进行比较并交换,直到满足堆的性质为止。
通过使用一维数组存储堆,可以方便地实现堆的各种操作,并且可以节省存储空间,提高访问效率。
堆的基本操作:
堆是一种常用的数据结构,它具有以下基本操作:
插入(Insertion):将一个新元素插入到堆中。插入操作通常用于将新元素添加到堆的末尾,并通过一系列交换操作将其移动到合适的位置,以保持堆的性质。对于最小堆,插入操作会将新元素插入到堆中并保持最小堆的性质;对于最大堆,则是保持最大堆的性质。
删除(Deletion):从堆中删除指定元素或者删除堆顶的元素。删除操作通常用于删除堆中的某个元素,并保持堆的性质不变。对于最小堆,删除操作通常删除堆顶的最小元素,并通过将堆的最后一个元素移动到堆顶,并通过一系列交换操作将其移动到合适的位置,以保持最小堆的性质。最大堆的删除操作也是类似的,只是操作的目标变成了删除堆顶的最大元素。
获取堆顶元素(Get Top):获取堆中的最小或最大元素,即堆顶的元素,而不进行删除操作。对于最小堆,获取堆顶元素即为获取堆中的最小元素;对于最大堆,则是获取堆中的最大元素。获取堆顶元素的时间复杂度为 O(1)。

🍓堆模板:
// h[N]存储堆中的值, h[1]是堆顶,x的左儿子是2x, 右儿子是2x + 1
// ph[k]存储第k个插入的点在堆中的位置
// hp[k]存储堆中下标是k的点是第几个插入的
int h[N], ph[N], hp[N], size;
// 交换两个点,及其映射关系
void heap_swap(int a, int b)
{
swap(ph[hp[a]],ph[hp[b]]);//
swap(hp[a], hp[b]);//交换所记录的在堆中插入的值的顺序
swap(h[a], h[b]);//交换堆中的值
}
void down(int u)
{
int t = u;
if (u * 2 <= size && h[u * 2] < h[t]) t = u * 2;
if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
if (u != t)
{
heap_swap(u, t);
down(t);
}
}
void up(int u)
{
while (u / 2 && h[u] < h[u / 2])
{
heap_swap(u, u / 2);
u >>= 1;
}
}
// O(n)建堆
for (int i = n / 2; i; i -- ) down(i);✨哈希表

一般哈希
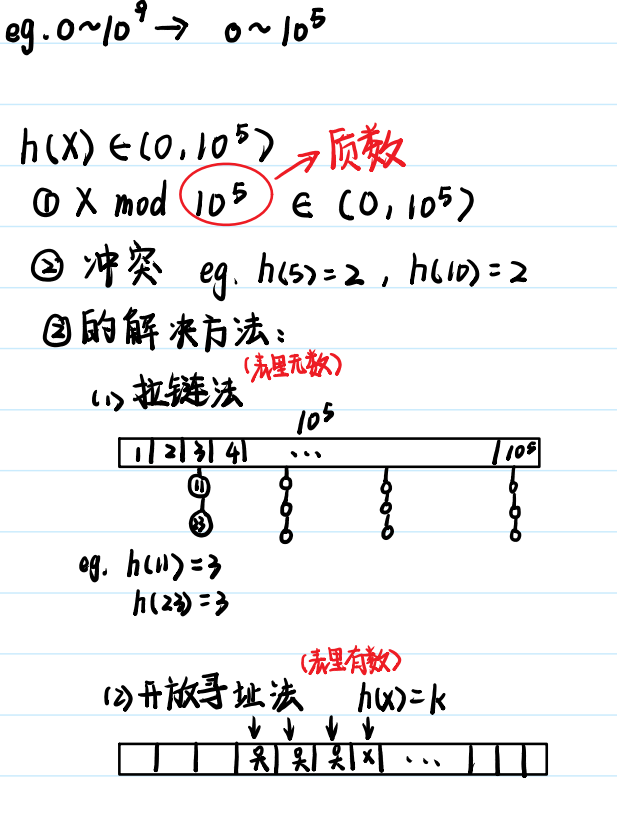
使用情况:将大范围数映射成小范围//哈希是把所有的数放在小空间存起来,然后解决冲突,离散化是把用到的抽取出来
🍓一般哈希模板:
(1) 拉链法
int h[N], e[N], ne[N], idx;
// 向哈希表中插入一个数
void insert(int x)
{
int k = (x % N + N) % N;
e[idx] = x;
ne[idx] = h[k];
h[k] = idx ++ ;
}
// 在哈希表中查询某个数是否存在
bool find(int x)
{
int k = (x % N + N) % N;
for (int i = h[k]; i != -1; i = ne[i])
if (e[i] == x)
return true;
return false;
}(2) 开放寻址法
int h[N];
// 如果x在哈希表中,返回x的下标;如果x不在哈希表中,返回x应该插入的位置
int find(int x)
{
int t = (x % N + N) % N;
while (h[t] != null && h[t] != x)
{
t ++ ;
if (t == N) t = 0;
}
return t;
}字符串哈希
字符串前缀哈希法//快速判断两个字符串是否相等
🍓字符串哈希模板:
🍒🍒核心思想:将字符串看成P进制数,P的经验值是131或13331,取这两个值的冲突概率低
🍒🍒小技巧:取模的数用2^64,这样直接用unsigned long long存储,溢出的结果就是取模的结果
typedef unsigned long long ULL;
ULL h[N], p[N]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
// 初始化
p[0] = 1;
for (int i = 1; i <= n; i ++ )
{
h[i] = h[i - 1] * P + str[i];
p[i] = p[i - 1] * P;
}
// 计算子串 str[l ~ r] 的哈希值
ULL get(int l, int r)
{
return h[r] - h[l - 1] * p[r - l + 1];
}