一、凸包检测

在这里插入图片描述
图中左侧为边缘检测的效果，中间为图像经过二值化的效果，右图为凸包检测效果。

convexHull(lnputArraypoints, OutputArray hull，bool clockwise = false, bool returnPoints = true)

points:输入的2D点集。
hull:输出凸包的顶点。
clockwise:方向标志，当参数为true时，凸包顺序为顺时针方向，否则为逆时针方向。
returnPoints:输出数据的类型标志，当参数为true时第二个参数输出的结果是凸包顶点的坐标，否则第二个参数输出的结果是凸包顶点的索引。
这里的计算实例如下：

int main() {

	//读取图片
	Mat src = imread("图片1.png");
	if (src.empty())
	{
		printf("不能打开空图片");
		return -1;
	}

	Mat gray, binary;
	//转化为灰度图
	cvtColor(src, gray, COLOR_BGR2GRAY);
	//二值化
	threshold(gray, binary, 105, 255, THRESH_BINARY);

	//开运算去除细小区域
	Mat k = getStructuringElement(MORPH_RECT, Size(3, 3), Point(-1, -1));
	morphologyEx(binary, binary, MORPH_RECT, k);

	//轮廓检测
	vector<vector<Point>>contours;
	//存放轮廓结构变量
	vector<Vec4i>hierarchy;

	findContours(binary, contours, hierarchy, 0, 2, Point());

	for (int i = 0; i < contours.size(); i++)
	{
		//计算凸包
		vector<Point>hull;
		convexHull(contours[i], hull);

		//绘制凸包
		for (int j = 0; j < hull.size(); j++)
		{
			//绘制凸包顶点
			circle(src, hull[j], 4, Scalar(255, 0, 0), 2, 8, 0);
			//连接凸包
			//将起始点与终点相连
			if (j == hull.size()-1)
			{
				line(src, hull[j], hull[0], Scalar(0, 0, 255), 2, 8, 0);
				break;
			}
			line(src, hull[j], hull[j+1], Scalar(0, 0, 255), 2, 8, 0);
		}
	}

	imshow("q", src);

	waitKey(0);
	return 0;
}

二、直线检测

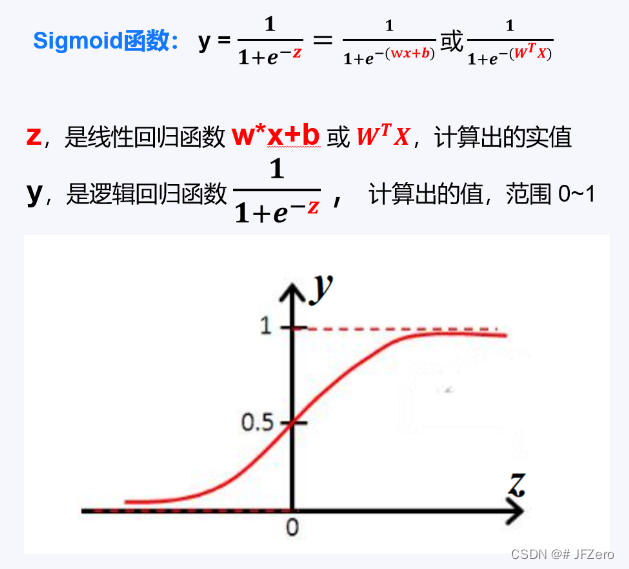
检测直线的霍夫变换原理：
在这里插入图片描述
先看左上角的图像，图中我们可以看出三条直线都经过了一个点。这里我们可以将y=kx+b一个函数描述这三条直线。由于都经过一个点，所以(x,y)的参数是固定的，右上角的图像为k、b的参数空间。也就是说参数空间中的每一个点都可以描述原空间的每一条直线。
在这里插入图片描述
上图中左上方图片可以看出，这三个点绘制成的直线没有斜率k，因此不能在参数空间上表示该直线。这时我们可以采用上图中的下部分的方法：可以用直线到坐标原点的距离，以及垂线与x轴的夹角来表示这一直线。
检测直线过程：
在这里插入图片描述
标准霍夫变换函数：

HoughLines(IlnputArray image, OutputArray lines,double rho, double theta, int threshold, double srn = 0, double stn = 0, double min_theta = 0, double max_theta = cv_PI)

image:目标图像。
lines: 检测直线的输出量。
rho：离散化后的单位长度。
theta：离散化后的单位角度。
threshold：步骤三中的阈值。
srn、stn：当两参数为0时，则为标准的霍夫变换，不为零则为多尺度霍夫变换。
min_theta、max_theta：角度最大最小值。
渐进概率式霍夫变换：

HoughllLinesP(InputArrayimage, OutputArray lines, double rho, double theta, int threshold, minLineLength =, void cv=HoughllLinesP( InputArrayimage, OutputArray lines.double 0, double maxLineGap = 0)

image:待检测直线的原图像，必须是CV_8C的单通道二值图像。
lines:霍夫变换检测到的直线输出量，每一条直线都由4个参数进行描述，分别是直线两个端点的坐标rho:以像素为单位的距离分辨率。
theta:以弧度为单位的角度分辨率。
threshold:累加器的阈值。
minLineLength:直线的最小长度，当检测直线的长度小于该数值时将会被剔除。
maxLineGap:允许将同一行两个点连接起来的最大距离。
标准霍夫变换应用案例：

void drawLine(Mat &img,  //原图像
	vector<Vec2f> lines, //检测的直线数据
	double rows, //原图的行数
	double cols,//原图的列数
	Scalar scalar, //绘制直线的颜色
	int n //绘制直线的线宽
	)
{
	Point pt1, pt2;
	for (size_t i = 0; i < lines.size(); i++)
	{
		float rho = lines[i][0]; //直线距离坐标原点的距离
		float theta = lines[i][1]; //直线过坐标原点垂线与x轴的夹角
		double a = cos(theta); //夹角的余弦值
		double b = sin(theta);//夹角的正弦值
		double x0 = a * rho, y0 = b * rho;//直角与过坐标原点的垂线交点
		double length = max(rows, cols); //  图像高度的最大值、计算直线上的一点

		pt1.x = cvRound(x0 + length * (-b));
		pt1.y = cvRound(y0 + length * (a));

		//计算直线上另一点
		pt2.x = cvRound(x0 - length * (-b));
		pt2.y = cvRound(y0 - length * (a));
		//两点绘制一条直线
		line(img, pt1, pt2, scalar, n);
	}


}

int main() {

	//以灰度图形式读取图片
	Mat src = imread("2.jpg", IMREAD_GRAYSCALE);
	if (src.empty())
	{
		printf("不能打开空图片");
		return -1;
	}

	//检测边缘图像，并二值化
	Mat edge;
	Canny(src, edge, 80, 180, 3, false);
	//进行二值化操作
	threshold(edge, edge, 170, 255, THRESH_BINARY);

	//使用累加器检测直线
	vector<Vec2f> line1, line2;
	HoughLines(edge, line1, 1, CV_PI / 180, 50, 0, 0);
	HoughLines(edge, line2, 1, CV_PI / 180, 150, 0, 0);

	//在原图中绘制直线
	Mat img1, img2;
	//深拷贝出两个原图像，对比两个变换的结果
	src.copyTo(img1);
	src.copyTo(img2);

	//绘制图像
	drawLine(img1, line1, edge.rows, edge.cols, Scalar(255), 2);
	drawLine(img2, line2, edge.rows, edge.cols, Scalar(255), 2);

	imshow("a", img1);
	imshow("b", img2);
	imshow("c", edge);
	waitKey(0);
	return 0;
}

运行上述的代码可以显示出如下三个图片：
边缘检测效果：
在这里插入图片描述
阈值较大的显示效果：

阈值较小的显示效果：

渐进概率霍夫变换应用案例：

int main() {

	//以灰度图形式读取图片
	Mat src = imread("2.jpg", IMREAD_GRAYSCALE);
	if (src.empty())
	{
		printf("不能打开空图片");
		return -1;
	}

	//检测边缘图像，并二值化
	Mat edge;
	Canny(src, edge, 80, 180, 3, false);

	//使用渐进式霍夫变换提取直线
	vector<Vec4i> linesP1, linesP2;
	//两个点连接最大距离10
	HoughLinesP(edge, linesP1, 1, CV_PI / 180, 150, 30, 10);
	//两个点连接最大距离30
	HoughLinesP(edge, linesP2, 1, CV_PI / 180, 150, 30, 30);

	//分别绘制两个不同阈值的直线
	Mat img1;
	src.copyTo(img1);
	for (size_t i = 0; i < linesP1.size(); i++)
	{
		line(img1, Point(linesP1[i][0], linesP1[i][1]), Point(linesP1[i][2], linesP1[i][3]), Scalar(255), 3);
	}

	imshow("q", img1);

	Mat img2;
	src.copyTo(img2);
	for (size_t i = 0; i < linesP2.size(); i++)
	{
		line(img2, Point(linesP2[i][0], linesP2[i][1]), Point(linesP2[i][2], linesP2[i][3]), Scalar(255), 3);
	}

	imshow("q", img1);
	imshow("w", img2);

	waitKey(0);
	return 0;
}