在上期,我给大家讲解了关于单个状态下的dp问题,本期我给大家讲述几道关于多状态下的dp问题。希望大家有所帮助!!!
目录
(一)粉刷房⼦
(二)买卖股票的最佳时机含冷冻期
(三)买卖股票的最佳时机含手续费
(一)粉刷房⼦
- 链接如下:剑指 Offer II 091. 粉刷房子
题⽬描述:

算法思路:
1. 状态表⽰:
对于线性 dp ,我们可以⽤「经验 + 题⽬要求」来定义状态表⽰:
- i. 以某个位置为结尾;
- ii. 以某个位置为起点。
这⾥我们选择⽐较常⽤的⽅式,以某个位置为结尾,结合题⽬要求,定义⼀个状态表⽰:
但是我们这个题在 i 位置的时候,会⾯临「红」「蓝」「绿」三种抉择,所依赖的状态需要细分:
- dp[i][0] 表⽰:粉刷到 i 位置的时候,最后⼀个位置粉刷上「红⾊」,此时的最⼩花 费;
- dp[i][1] 表⽰:粉刷到 i 位置的时候,最后⼀个位置粉刷上「蓝⾊」,此时的最⼩花 费;
- dp[i][2] 表⽰:粉刷到 i 位置的时候,最后⼀个位置粉刷上「绿⾊」,此时的最⼩花 费。
2. 状态转移⽅程:
因为状态表⽰定义了三个,因此我们的状态转移⽅程也要分析三个:
对于 dp[i][0] :
- 如果第 i 个位置粉刷上「红⾊」,那么 i - 1 位置上可以是「蓝⾊」或者「绿⾊」
- 因此我们 需要知道粉刷到 i - 1 位置上的时候,粉刷上「蓝⾊」或者「绿⾊」的最⼩花费,然后加上 i 位置的花费即可;
- 于是状态转移⽅程为: dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i - 1][0]
同理,我们可以推导出另外两个状态转移⽅程为:
- dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i - 1][1] ;
- dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + costs[i - 1][2] 。
3. 初始化:
可以在最前⾯加上⼀个「辅助结点」,帮助我们初始化。
使⽤这种技巧要注意两个点:
- i. 辅助结点⾥⾯的值要「保证后续填表是正确的」;
- ii. 「下标的映射关系」。 在本题中,添加⼀个节点,并且初始化为 0 即可。
4. 填表顺序
根据「状态转移⽅程」得「从左往右,三个表⼀起填」
5. 返回值
- 根据「状态表⽰」,应该返回最后⼀个位置粉刷上三种颜⾊情况下的最⼩值;
- 因此需要返回: min(dp[n][0], min(dp[n][1], dp[n][2]))
代码展示:
class Solution {
public:
int minCost(vector<vector<int>>& costs) {
int size = costs.size();
vector<vector<int>> dp(size + 1, vector<int>(3));
for (int i = 1; i <= size; i++) {
dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i - 1][0];
dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i - 1][1];
dp[i][2] = min(dp[i - 1][1], dp[i - 1][0]) + costs[i - 1][2];
}
return min(dp[size][0], min(dp[size][1], dp[size][2]));
}
};- Leetcode 测试结果:

性能分析:
- 时间复杂度:O(n)。其中 n 是房子个数。需要遍历全部房子一次,由于颜色数量固定是三种,因此对于每个房子计算粉刷房子的最小花费成本的时间是 O(1),总时间复杂度是 O(n)。
- 空间复杂度:O(n).
(二)买卖股票的最佳时机含冷冻期
- 链接如下:309. 最佳买卖股票时机含冷冻期
在之前我已经对买卖股票的最佳时机等进行了具体的探讨,如果大家对于不清楚的话,可以去看我关于买卖股票最佳时机的题目讲解:买卖股票最佳时机类题目讲解
题目描述

算法思路:
1. 状态表⽰:
对于线性 dp ,我们可以⽤「经验 + 题⽬要求」来定义状态表⽰:
- i. 以某个位置为结尾;
- ii. 以某个位置为起点。
这⾥我们选择⽐较常⽤的⽅式,以某个位置为结尾,结合题⽬要求,定义⼀个状态表⽰:
由于有「买⼊」「可交易」「冷冻期」三个状态,因此我们可以选择⽤三个数组,其中:
- dp[i][0] 表⽰:第 i 天结束后,处于「买⼊」状态,此时的最⼤利润;
- dp[i][1] 表⽰:第 i 天结束后,处于「可交易」状态,此时的最⼤利润;
- dp[i][2] 表⽰:第 i 天结束后,处于「冷冻期」状态,此时的最⼤利润。
2. 状态转移⽅程:
我们要谨记规则:
i. 处于「买⼊」状态的时候,我们现在有股票,此时不能买股票,只能继续持有股票,或者卖 出股票;
ii. 处于「卖出」状态的时候:
- 如果「在冷冻期」,不能买⼊;
- 如果「不在冷冻期」,才能买⼊。
对于 dp[i][0] ,我们有「两种情况」能到达这个状态:
- i. 在 i - 1 天持有股票,此时最⼤收益应该和 i - 1 天的保持⼀致: dp[i - 1] [0] ;
- ii. 在 i 天买⼊股票,那我们应该选择 i - 1 天不在冷冻期的时候买⼊,由于买⼊需要花 钱,所以此时最⼤收益为: dp[i - 1][1] - prices[i]
两种情况应取最⼤值,因此: dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]) 。
对于 dp[i][1] ,我们有「两种情况」能到达这个状态:
- i. 在 i - 1 天的时候,已经处于冷冻期,然后啥也不⼲到第 i 天,此时对应的状态为: dp[i - 1][2] ;
- ii. 在 i - 1 天的时候,⼿上没有股票,也不在冷冻期,但是依旧啥也不⼲到第 i 天,此时 对应的状态为 dp[i - 1][1] ;
两种情况应取最⼤值,因此: dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]) 。
对于 dp[1][i] ,我们只有「⼀种情况」能到达这个状态:
- i. 在 i - 1 天的时候,卖出股票。 因此对应的状态转移为: dp[i][2] = dp[i - 1][0] + prices[i]
3. 初始化:
三种状态都会⽤到前⼀个位置的值,因此需要初始化每⼀⾏的第⼀个位置:
- dp[0][0] :此时要想处于「买⼊」状态,必须把第⼀天的股票买了,因此 dp[0][0] = - prices[0]
- dp[0][1] :啥也不⽤⼲即可,因此 dp[0][1] = 0 ;
- dp[0][2] :⼿上没有股票,买⼀下卖⼀下就处于冷冻期,此时收益为 0 ,因此 dp[0][2] = 0 。
4. 填表顺序:
- 根据「状态表⽰」,我们要三个表⼀起填,每⼀个表「从左往右」。
5. 返回值:
- 应该返回「卖出状态」下的最⼤值,因此应该返回 max(dp[n - 1][1], dp[n - 1] [2]) 。
代码展示
class Solution {
public:
int maxProfit(vector<int>& prices) {
int size = prices.size();
vector<vector<int>> dp(size, vector<int>(3));
dp[0][0] = -prices[0];
for(int i = 1; i < size; i++)
{
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);
dp[i][2] = dp[i - 1][0] + prices[i];
}
return max(dp[size - 1][1], dp[size - 1][2]);
}
};- Leetcode 测试结果:

性能分析:
- 时间复杂度:O(n)。
- 空间复杂度:O(n).
(三)买卖股票的最佳时机含手续费
- 链接如下:714. 买卖股票的最佳时机含手续费
题目描述

算法思路
1. 状态表⽰:
对于线性 dp ,我们可以⽤「经验 + 题⽬要求」来定义状态表⽰:
- i. 以某个位置为结尾,巴拉巴拉;
- ii. 以某个位置为起点,巴拉巴拉。
这⾥我们选择⽐较常⽤的⽅式,以某个位置为结尾,结合题⽬要求,定义⼀个状态表⽰:
由于有「买⼊」「可交易」两个状态,因此我们可以选择⽤两个数组,其中:
- f[i] 表⽰:第 i 天结束后,处于「买⼊」状态,此时的最⼤利润;
- g[i] 表⽰:第 i 天结束后,处于「卖出」状态,此时的最⼤利润。
2. 状态转移⽅程:
我们选择在「卖出」的时候,⽀付这个⼿续费,那么在「买⼊」的时候,就不⽤再考虑⼿续费的问 题。
对于 f[i] ,我们有两种情况能到达这个状态:
- i. 在 i - 1 天「持有」股票,第 i 天啥也不⼲。此时最⼤收益为 f[i - 1] ;
- ii. 在 i - 1 天的时候「没有」股票,在第 i 天买⼊股票。此时最⼤收益为 g[i - 1] - prices[i]) ;
两种情况下应该取最⼤值,因此 f[i] = max(f[i - 1], g[i - 1] - prices[i])
对于 g[i] ,我们也有两种情况能够到达这个状态:
- i. 在 i - 1 天「持有」股票,但是在第 i 天将股票卖出。此时最⼤收益为: f[i - 1] + prices[i] - fee) ,记得⼿续费;
- ii. 在 i - 1 天「没有」股票,然后第 i 天啥也不⼲。此时最⼤收益为: g[i - 1] ; 两种情况下应该取最⼤值,因此 g[i] = max(g[i - 1], f[i - 1] + prices[i] - fee) 。
3. 初始化:
由于需要⽤到前⾯的状态,因此需要初始化第⼀个位置。
- 对于 f[0] ,此时处于「买⼊」状态,因此 f[0] = -prices[0] ;
- 对于 g[0] ,此时处于「没有股票」状态,啥也不⼲即可获得最⼤收益,因此 g[0] = 0 。
4. 填表顺序:
- 毫⽆疑问是「从左往右」,但是两个表需要⼀起填。
5. 返回值:
- 应该返回「卖出」状态下,最后⼀天的最⼤值收益: g[n - 1] 。
代码展示
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int size = prices.size();
vector<int> f(size);
auto g = f;
f[0] = -prices[0];
for(int i = 1; i < size; i++){
f[i] = max(f[i - 1], g[i - 1] - prices[i]);
g[i] = max(g[i - 1], f[i - 1] + prices[i] - fee);
}
return g[size - 1];
}
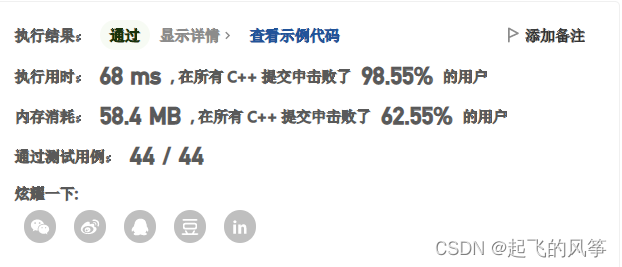
};- Leetcode 测试结果:
性能分析:
- 时间复杂度:O(n)。
- 空间复杂度:O(1).
以上便是关于简单多状态 dp 的三道题目的讲解。希望对大家有所帮助,感谢大家的阅读!!!