二分类-逻辑回归模型
1.模型函数
1)多元线性回归函数:
Z
^
计算
=
X
W
T
\hat{Z}_{计算} = XW^T
Z^计算=XWT
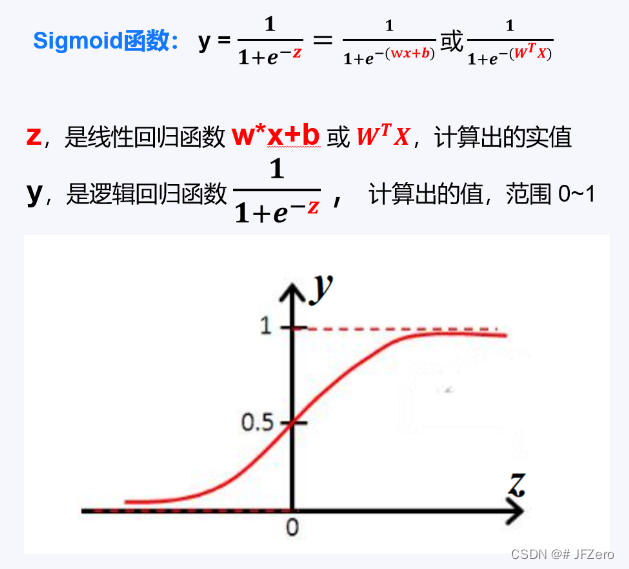
2)softmax函数:
Y
^
模型
=
S
i
g
m
o
i
d
(
Z
^
计算
)
=
1
1
+
e
−
Z
^
计算
\hat{Y}_{模型} =Sigmoid(\hat{Z}_{计算})= \frac{1}{1+e^{-\hat{Z}_{计算}}}
Y^模型=Sigmoid(Z^计算)=1+e−Z^计算1
👉已知数据:实际Y值=
[
y
0
y
1
y
2
y
3
.
.
.
y
n
]
\begin{bmatrix}y_0\\y_1\\y_2\\y_3\\...\\y_n\end{bmatrix}
y0y1y2y3...yn
,X=
[
x
00
,
x
10
.
.
.
x
m
0
x
01
,
x
11
.
.
.
x
m
1
x
02
,
x
12
.
.
.
x
m
2
x
03
,
x
13
.
.
.
x
m
3
.
.
.
x
0
n
,
x
1
n
.
.
.
x
m
n
]
\begin{bmatrix}x_{00},x_{10}...x_{m0}\\x_{01},x_{11}...x_{m1}\\x_{02},x_{12}...x_{m2}\\x_{03},x_{13}...x_{m3}\\...\\x_{0n},x_{1n}...x_{mn}\end{bmatrix}
x00,x10...xm0x01,x11...xm1x02,x12...xm2x03,x13...xm3...x0n,x1n...xmn
👉未知数据:有如下3组未知数据
①模型参数 W =
[
w
0
,
w
1
,
w
2
,
w
3
,
.
.
.
,
w
m
]
\begin{bmatrix}w_0,w_1,w_2,w_3,...,w_m\end{bmatrix}
[w0,w1,w2,w3,...,wm]
②线性函数计算
Z
^
计算
=
X
W
T
=
[
x
00
,
x
10
.
.
.
x
m
0
x
01
,
x
11
.
.
.
x
m
1
x
02
,
x
12
.
.
.
x
m
2
x
03
,
x
13
.
.
.
x
m
3
.
.
.
x
0
n
,
x
1
n
.
.
.
x
m
n
]
[
w
0
w
1
w
2
w
3
.
.
.
w
m
]
=
[
z
0
^
z
1
^
z
2
^
z
3
^
.
.
.
z
n
^
]
\hat{Z}_{计算}=XW^T=\begin{bmatrix}x_{00},x_{10}...x_{m0}\\x_{01},x_{11}...x_{m1}\\x_{02},x_{12}...x_{m2}\\x_{03},x_{13}...x_{m3}\\...\\x_{0n},x_{1n}...x_{mn}\end{bmatrix}\begin{bmatrix}w_0\\w_1\\w_2\\w_3\\...\\w_m\end{bmatrix}=\begin{bmatrix}\hat{z_0}\\\hat{z_1}\\\hat{z_2}\\\hat{z_3}\\...\\\hat{z_n}\end{bmatrix}
Z^计算=XWT=
x00,x10...xm0x01,x11...xm1x02,x12...xm2x03,x13...xm3...x0n,x1n...xmn
w0w1w2w3...wm
=
z0^z1^z2^z3^...zn^
③模型分类 Y ^ = S i g m o i d ( Z ^ ) = [ 1 1 + e − z 0 ^ 1 1 + e − z 1 ^ 1 1 + e − z 2 ^ 1 1 + e − z 3 ^ . . . 1 1 + e − z n ^ ] = [ y 0 ^ y 1 ^ y 2 ^ y 3 ^ . . . y n ^ ] \hat{Y}=Sigmoid(\hat{Z})=\begin{bmatrix} \frac{1}{1+e^{-\hat{z_0}}}\\\frac{1}{1+e^{-\hat{z_1}}}\\\frac{1}{1+e^{-\hat{z_2}}}\\\frac{1}{1+e^{-\hat{z_3}}}\\...\\\frac{1}{1+e^{-\hat{z_n}}}\end{bmatrix}=\begin{bmatrix}\hat{y_0}\\ \hat{y_1}\\\hat{y_2}\\\hat{y_3}\\...\\\hat{y_n}\end{bmatrix} Y^=Sigmoid(Z^)= 1+e−z0^11+e−z1^11+e−z2^11+e−z3^1...1+e−zn^1 = y0^y1^y2^y3^...yn^
y
^
i
值为
0
到
1
的小数,例如
0.4
,表示分类为
1
的概率是
0.4
\hat{y}_i值为0到1的小数,例如0.4,表示分类为 1 的概率是0.4
y^i值为0到1的小数,例如0.4,表示分类为1的概率是0.4
2.损失函数
逻辑回归模型的损失函数,采用极大似然估计法
L
o
s
s
=
−
∑
i
=
0
n
(
y
i
^
.
l
n
y
i
+
(
1
−
y
i
^
)
.
l
n
y
i
)
Loss = -\sum_{i=0}^{n}{(\hat{y_{i}}.lny_{i}+(1-\hat{y_{i}}).lny_{i}})
Loss=−∑i=0n(yi^.lnyi+(1−yi^).lnyi)
2.1 极大似然估计法的公式推导
二分类,指实际只有两种互斥的类别:要么是男,要么是女(要么A类,要么B类)
这就是个典型的0-1分布(伯努利分布)
| 分类 | y=0 | y=1 |
|---|---|---|
| 计算出的分类概率 | 1 − y ^ 1-\hat{y} 1−y^ | y ^ \hat{y} y^ |
单次分类正确的概率为: y ^ 计算 y ∗ ( 1 − y ^ 计算 ) ( 1 − y ) \hat{y}_{计算}^y*(1-\hat{y}_{计算})^{(1-y)} y^计算y∗(1−y^计算)(1−y)
- 实际分类为y=1时,分类正确的概率为 y ^ 计算 y ∗ ( 1 − y ^ 计算 ) ( 1 − y ) \hat{y}_{计算}^y*(1-\hat{y}_{计算})^{(1-y)} y^计算y∗(1−y^计算)(1−y)= y ^ \hat{y} y^
- 实际分类为y=0时,分类正确的概率为 y ^ 计算 y ∗ ( 1 − y ^ 计算 ) ( 1 − y ) \hat{y}_{计算}^y*(1-\hat{y}_{计算})^{(1-y)} y^计算y∗(1−y^计算)(1−y)= 1 − y ^ 1-\hat{y} 1−y^
无论实际分类是y=0还是y=1,我们都希望模型分类正确的概率达到最大!
👉即求出
y
^
计算
y
∗
(
1
−
y
^
计算
)
(
1
−
y
)
\hat{y}_{计算}^y*(1-\hat{y}_{计算})^{(1-y)}
y^计算y∗(1−y^计算)(1−y)的最大值。
即为分类正确的概率:即为似然值——表示基于实际分布下,模型分类正确的概率值
y
^
计算
y
∗
(
1
−
y
^
计算
)
(
1
−
y
)
\hat{y}_{计算}^y*(1-\hat{y}_{计算})^{(1-y)}
y^计算y∗(1−y^计算)(1−y),可以转化为
l
n
(
x
)
ln(x)
ln(x)函数,因为
l
n
(
x
)
ln(x)
ln(x)是单调递增函数,那么只要x越大,则
l
n
(
x
)
ln(x)
ln(x)也越大。
因此
y
^
计算
y
∗
(
1
−
y
^
计算
)
(
1
−
y
)
\hat{y}_{计算}^y*(1-\hat{y}_{计算})^{(1-y)}
y^计算y∗(1−y^计算)(1−y)则变为👇
l n ( y ^ 计算 y ∗ ( 1 − y ^ 计算 ) ( 1 − y ) ) = y l n ( y ^ 计算 ) + ( 1 − y ) l n ( 1 − y ^ 计算 ) ln(\hat{y}_{计算}^y*(1-\hat{y}_{计算})^{(1-y)})=yln(\hat{y}_{计算})+(1-y)ln(1-\hat{y}_{计算}) ln(y^计算y∗(1−y^计算)(1−y))=yln(y^计算)+(1−y)ln(1−y^计算)
求出
y
l
n
(
y
^
计算
)
+
(
1
−
y
)
l
n
(
1
−
y
^
计算
)
yln(\hat{y}_{计算})+(1-y)ln(1-\hat{y}_{计算})
yln(y^计算)+(1−y)ln(1−y^计算)的最大值即可,这正是极大似然估计法
但我们习惯转化为损失函数,求损失函数的极小值,因此可在函数前加负号即可:
L o s s = − [ y l n ( y ^ 计算 ) + ( 1 − y ) l n ( 1 − y ^ 计算 ) ] Loss = - [ yln(\hat{y}_{计算})+(1-y)ln(1-\hat{y}_{计算})] Loss=−[yln(y^计算)+(1−y)ln(1−y^计算)],求出Loss的极小值,即可使单次分类正确率达到最大
那么,要使所有分类的正确率达到最大,即将每次分类的Loss值累加:
L o s s 总 = − ∑ i = 0 n y l n ( y ^ 计算 ) + ( 1 − y ) l n ( 1 − y ^ 计算 ) Loss_总=- \sum_{i=0}^{n}yln(\hat{y}_{计算})+(1-y)ln(1-\hat{y}_{计算}) Loss总=−∑i=0nyln(y^计算)+(1−y)ln(1−y^计算)
多分类-逻辑回归模型
1. 模型函数
1)多元线性回归函数:
Z
^
计算
=
X
W
T
\hat{Z}_{计算} = XW^T
Z^计算=XWT
2)softmax函数:
Y
^
模型
=
s
o
f
t
m
a
x
(
Z
^
计算
)
=
1
1
+
e
−
Z
^
计算
\hat{Y}_{模型} =softmax(\hat{Z}_{计算})= \frac{1}{1+e^{-\hat{Z}_{计算}}}
Y^模型=softmax(Z^计算)=1+e−Z^计算1
👉已知数据:实际Y值=
[
y
0
y
1
y
2
y
3
.
.
.
y
n
]
\begin{bmatrix}y_0\\y_1\\y_2\\y_3\\...\\y_n\end{bmatrix}
y0y1y2y3...yn
,X=
[
x
00
,
x
10
.
.
.
x
m
0
x
01
,
x
11
.
.
.
x
m
1
x
02
,
x
12
.
.
.
x
m
2
x
03
,
x
13
.
.
.
x
m
3
.
.
.
x
0
n
,
x
1
n
.
.
.
x
m
n
]
\begin{bmatrix}x_{00},x_{10}...x_{m0}\\x_{01},x_{11}...x_{m1}\\x_{02},x_{12}...x_{m2}\\x_{03},x_{13}...x_{m3}\\...\\x_{0n},x_{1n}...x_{mn}\end{bmatrix}
x00,x10...xm0x01,x11...xm1x02,x12...xm2x03,x13...xm3...x0n,x1n...xmn
👉未知数据: 如果原数据共有 k+1 个类别,则有如下未知数据
①模型参数 W=
[
w
00
,
w
10
,
.
.
.
,
w
m
0
w
01
,
w
11
,
.
.
.
,
w
m
1
w
02
,
w
12
,
.
.
.
,
w
m
2
.
.
.
w
0
k
,
w
1
k
,
.
.
.
,
w
m
k
]
\begin{bmatrix}w_{00},w_{10},...,w_{m0}\\w_{01},w_{11},...,w_{m1}\\w_{02},w_{12},...,w_{m2}\\...\\w_{0k},w_{1k},...,w_{mk}\end{bmatrix}
w00,w10,...,wm0w01,w11,...,wm1w02,w12,...,wm2...w0k,w1k,...,wmk
②计算
Z
^
n
×
k
=
X
(
n
×
m
)
W
m
×
k
T
=
[
z
00
^
,
z
01
^
,
.
.
.
,
z
0
k
^
z
10
^
,
z
11
^
,
.
.
.
,
z
1
k
^
z
20
^
,
z
21
^
,
.
.
.
,
z
2
k
^
.
.
.
z
n
0
^
,
z
n
1
^
,
.
.
.
,
z
n
k
^
]
\hat{Z} _{n×k}= {X_{(n×m)}W^T_{m×k}}=\begin{bmatrix}\hat{z_{00}},\hat{z_{01}},...,\hat{z_{0k}}\\ \hat{z_{10}},\hat{z_{11}},...,\hat{z_{1k}}\\\hat{z_{20}},\hat{z_{21}},...,\hat{z_{2k}}\\...\\\hat{z_{n0}},\hat{z_{n1}},...,\hat{z_{nk}}\end{bmatrix}
Z^n×k=X(n×m)Wm×kT=
z00^,z01^,...,z0k^z10^,z11^,...,z1k^z20^,z21^,...,z2k^...zn0^,zn1^,...,znk^
③模型分类
Y
^
=
S
o
f
t
m
a
x
(
Z
)
=
[
e
z
i
j
∑
j
=
1
k
e
z
i
j
]
=
[
e
z
00
∑
j
=
1
k
e
z
0
j
,
e
z
01
∑
j
=
1
k
e
z
0
j
,
.
.
.
,
e
z
0
k
∑
j
=
1
k
e
z
0
j
e
z
10
∑
j
=
1
k
e
z
1
j
,
e
z
11
∑
j
=
1
k
e
z
1
j
,
.
.
.
,
e
z
1
k
∑
j
=
1
k
e
z
1
j
e
z
20
∑
j
=
1
k
e
z
2
j
,
e
z
21
∑
j
=
1
k
e
z
2
j
,
.
.
.
,
e
z
2
k
∑
j
=
1
k
e
z
2
j
.
.
.
e
z
n
0
∑
j
=
1
k
e
z
n
j
,
e
z
n
1
∑
j
=
1
k
e
z
n
j
,
.
.
.
,
e
z
n
k
∑
j
=
1
k
e
z
n
j
]
=
[
y
00
^
,
y
01
^
,
.
.
.
,
y
0
k
^
y
10
^
,
y
11
^
,
.
.
.
,
y
1
k
^
y
20
^
,
y
21
^
,
.
.
.
,
y
2
k
^
.
.
.
y
n
0
^
,
y
n
1
^
,
.
.
.
,
y
n
k
^
]
\hat{Y}=Softmax(Z)=\begin{bmatrix}\frac{e^{z_{ij}}}{\sum_{j=1}^ke^{z_{ij}}}\end{bmatrix}=\begin{bmatrix} \frac{e^{z_{00}}}{\sum_{j=1}^ke^{z_{0j}}},\frac{e^{z_{01}}}{\sum_{j=1}^ke^{z_{0j}}},...,\frac{e^{z_{0k}}}{\sum_{j=1}^ke^{z_{0j}}}\\\\ \frac{e^{z_{10}}}{\sum_{j=1}^ke^{z_{1j}}},\frac{e^{z_{11}}}{\sum_{j=1}^ke^{z_{1j}}},...,\frac{e^{z_{1k}}}{\sum_{j=1}^ke^{z_{1j}}}\\\\ \frac{e^{z_{20}}}{\sum_{j=1}^ke^{z_{2j}}},\frac{e^{z_{21}}}{\sum_{j=1}^ke^{z_{2j}}},...,\frac{e^{z_{2k}}}{\sum_{j=1}^ke^{z_{2j}}}\\\\...\\\\ \frac{e^{z_{n0}}}{\sum_{j=1}^ke^{z_{nj}}},\frac{e^{z_{n1}}}{\sum_{j=1}^ke^{z_{nj}}},...,\frac{e^{z_{nk}}}{\sum_{j=1}^ke^{z_{nj}}}\\ \end{bmatrix}= \begin{bmatrix}\hat{y_{00}},\hat{y_{01}},...,\hat{y_{0k}}\\ \\\hat{y_{10}},\hat{y_{11}},...,\hat{y_{1k}}\\\\ \hat{y_{20}},\hat{y_{21}},...,\hat{y_{2k}}\\\\...\\\\ \hat{y_{n0}},\hat{y_{n1}},...,\hat{y_{nk}}\end{bmatrix}
Y^=Softmax(Z)=[∑j=1kezijezij]=
∑j=1kez0jez00,∑j=1kez0jez01,...,∑j=1kez0jez0k∑j=1kez1jez10,∑j=1kez1jez11,...,∑j=1kez1jez1k∑j=1kez2jez20,∑j=1kez2jez21,...,∑j=1kez2jez2k...∑j=1keznjezn0,∑j=1keznjezn1,...,∑j=1keznjeznk
=
y00^,y01^,...,y0k^y10^,y11^,...,y1k^y20^,y21^,...,y2k^...yn0^,yn1^,...,ynk^
问题:
模型计算出的
Y
^
=
[
y
00
^
,
y
01
^
,
.
.
.
,
y
0
k
^
y
10
^
,
y
11
^
,
.
.
.
,
y
1
k
^
y
20
^
,
y
21
^
,
.
.
.
,
y
2
k
^
.
.
.
y
n
0
^
,
y
n
1
^
,
.
.
.
,
y
n
k
^
]
,实际
Y
值
=
[
y
0
y
1
y
2
y
3
.
.
.
y
n
]
模型计算出的 \hat{Y} =\begin{bmatrix}\hat{y_{00}},\hat{y_{01}},...,\hat{y_{0k}}\\ \\\hat{y_{10}},\hat{y_{11}},...,\hat{y_{1k}}\\\\ \hat{y_{20}},\hat{y_{21}},...,\hat{y_{2k}}\\\\...\\\\ \hat{y_{n0}},\hat{y_{n1}},...,\hat{y_{nk}}\end{bmatrix},实际Y值=\begin{bmatrix}y_0\\y_1\\y_2\\y_3\\...\\y_n\end{bmatrix}
模型计算出的Y^=
y00^,y01^,...,y0k^y10^,y11^,...,y1k^y20^,y21^,...,y2k^...yn0^,yn1^,...,ynk^
,实际Y值=
y0y1y2y3...yn
,如何进行比较?极大似然估计法如何计算??