第二章. Learning to Answer Yes_No
2.1 Perceptron Hypothesis Set
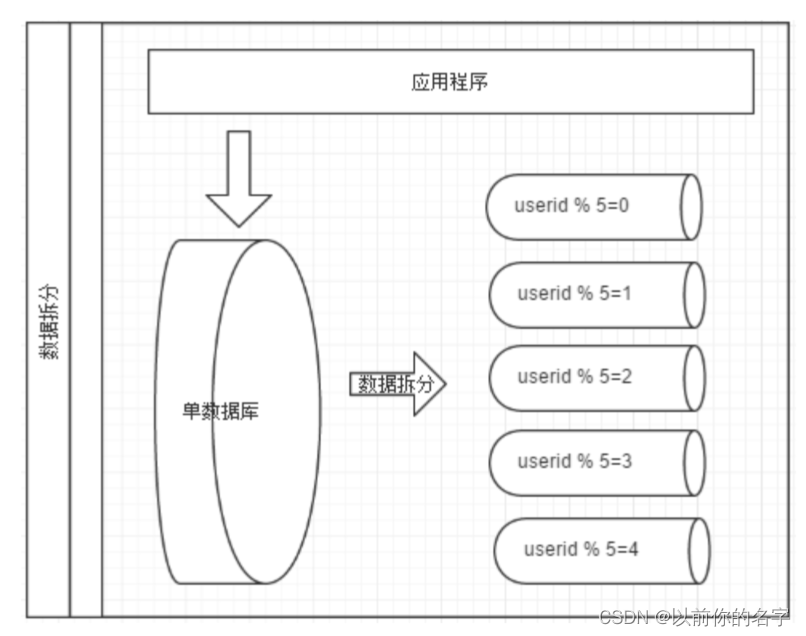
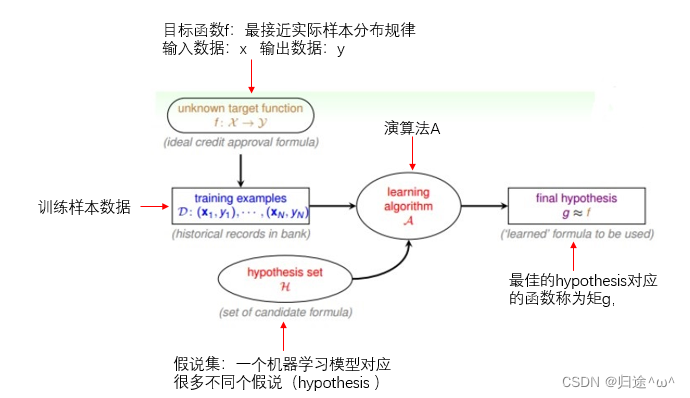
1.机器学习流程图:
在机器学习的整个流程中,模型的选择(Hypothesis Set)是非常重要的,它决定了机器学习的最终效果。
2.常用的机器学习模型——感知机(Perceptron)
1).语言描述:
以银行是否给用户发放信用卡为例,把用户的个人信息作为特征向量x,特征向量中共有n个特征,每个特征赋予一个权值w,表示特征对是否发放信用卡的影响程度,在这个过程中我们的目的就是为了计算出权值w和阈值threshold
①.使用sign函数,若所有特征加权和的值 ≥ 设定的阈值threshold,h(x)=1,发放信用卡;
②.使用sign函数,若所有特征加权和的值 < 设定的阈值threshold,h(x)=-1,不发放信用卡;
2).公式描述:

①.简化h(x)公式
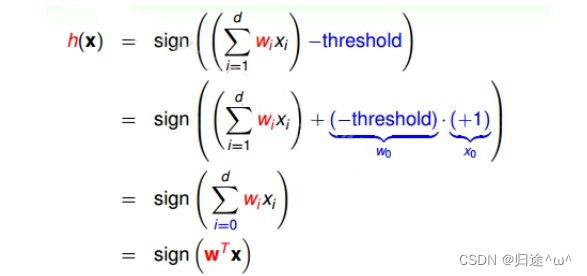
3).举例描述:
假设感知机模型是在一个二维的平面上h(x)=sign(w0+w1x+w2x2),其中w0+w1x+w2x2=0在平面上是一条分类直线,对正类(+1)和负类(-1)进行分类,权重w不同,对应于平面上的不同直线。

注意事项:感知器线性分类不限定在二维空间中,在3D中,线性分类用平面表示,在更高维度中,线性分类用超平面表示。
2.2 Perceptron Learning Algorithm(PLA)
在2.1节中我们已经知道了hypothesis set是由很多条直线构成。我们的目的是如何设计一个演算法A,来选择其中一条最好的直线,能将平面中的所有正负点进行正确分类,也就是找到最好的g,使g无限趋近于f。
1.PLA的思想:
1).语言描述:
在平面上随意选取一条直线进行分类,然后找到第一个分类错误的点进行修正,即变换分类直线的位置,通过不断迭代来对每次变换直线后的错误点进行逐点修正,直至分类完全正确,就得到了最好的直线,这就是PLA的思想。
①.修正的方法: (o代表+1,x:代表-1)
i).正确的类别为+1,误判到-1类别的情况:代表x,w之间的夹角角度过大,修正的方法就是使x,w的夹角小于90°(其中w是直线的法向量),通常做法是使 w <- w+yx (y=+1),来对误分类为负类的错误点进行修正
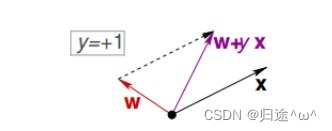
ii).正确的类别为-1,误判到+1类别的情况:代表x,w之间的夹角角度过小,修正的方法就是使x,w的夹角大于90°(其中w是直线的法向量),通常做法是使 w <- w+yx (y=-1),来对误分类为正类的错误点进行修正
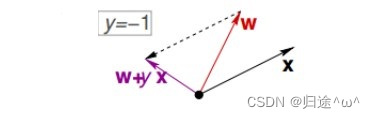
2).公式描述:
在实际操作中,逐点遍历,发现分类错误的点就进行修正,直至所有点全部分类正确,这种被称为circle PLA。

3).图解描述:
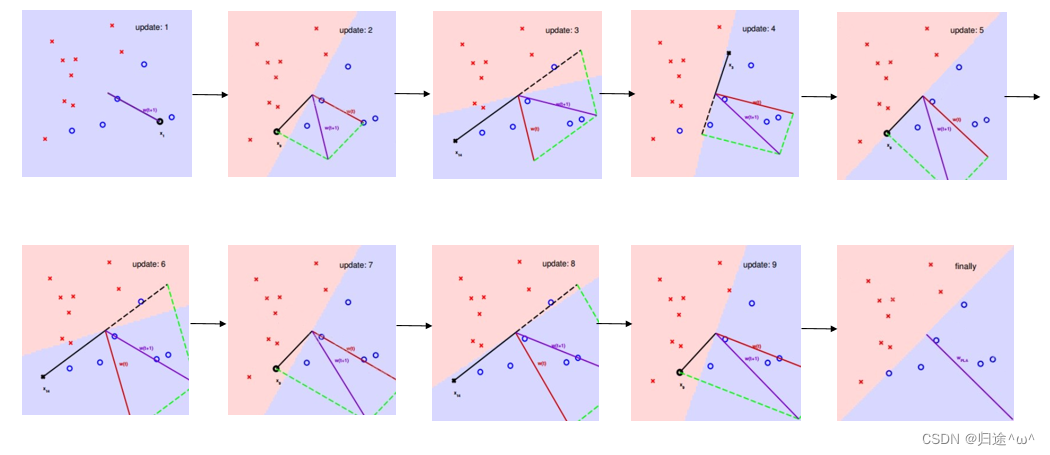
2.PLA的需要考虑的一个问题:
1).PLA迭代一定会停下来吗?如果线性不可分怎么办?
当找到一条最佳直线,能将平面上的所有点正确分类,那么PLA就停止了,要达到这个终止条件,需要确保数据是线性可分的。如果是非线性可分的,那么,PLA就不会停止。
2.3 Guarantee of PLA
1.线性可分与不可分的情况
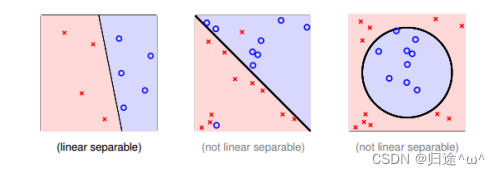
2.公式推导
对于线性可分的情况,如果存在这样一条直线,能够将正类(o)和负类(+)完全分开,令这时候的目标权重为Wf ,则对每个点,必然满足yn =sign(wTfxn).
1).对任一点都存在这样的关系式:
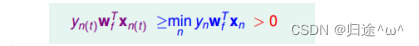
说明:
①.wTfxn:代表每个点与直线之间的距离:两个向量的内积,其中wf是直线的法向量,θ=90°(既然Wf是目标权重,代表所有点的分类均是正确的,所以点不可能在线上或者有错误点的点,与直线都存在一定的距离)
②.ynwTfxn:这个结果必定是>0的,因为所有点的分类均是正确的,yn和wTfxn值的符号一定是相同的。
③.min->n:与直线最近的点
④.t:代表第t次迭代
2).衡量 wt+1与wf越来越接近的两个条件:
①.证明wt+1与wf的内积大小。内积越大wt+1越接近目标权重wf.

结论:
从推导可以看出,wt+1与wf的内积比wt与wf的内积更大一些,表明了wt+1是在接近目标权重wf。
②.证明wt+1与wf向量长度的关系。wt+1与wf向量长度差异越小越好

说明:
①.只有点被误判的情况下,才需要变换分类直线的位置,那必然存在yn和wTfxn值的符号不一致,故两数的乘积必然是≤0的。
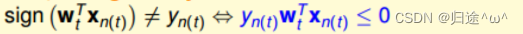
结论:
从推导可以看出,||w2t+1||相比||w2t||的增常量不超过max||x2n ||,wt的增长被限制了,||wt+1||与||wt||向量长度不会差别太大。
3).若令初始权重值w0=0(因为我们的分类标签是+1和-1,设置的阈值为0),那么经过T次修正后,有如下不等式关系:
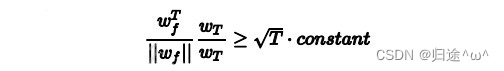
①.结论:
不等式左边是wt与wf夹角的余弦值,随着T的增大,余弦值越来越接近1,wt与wf越来越接近。同时需要注意的是√T·constant≤1,也就是说迭代次数T是有上界的,因从PLA最终会停下来,实现对线性数据的分类。
②.推导过程:


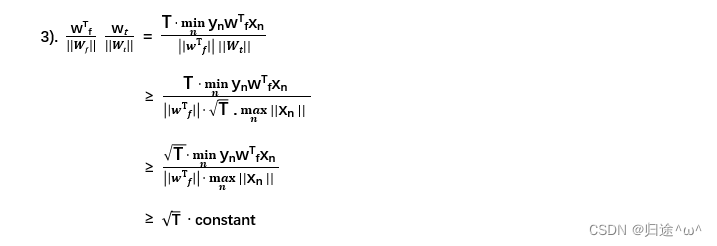
2.4 Non-Separable Data
对于非线性可分的数据,wf并不存在,PLA不一定会停下来,但是我们可以把分类错误的点当成在数据集中掺杂了noise,在实际的数据集中或多或少掺杂noise,我们引入了Pocket Algorithm(PLA的修改版本)算法来解决非线性分类问题。
1.掺杂noise后的机器学习流程
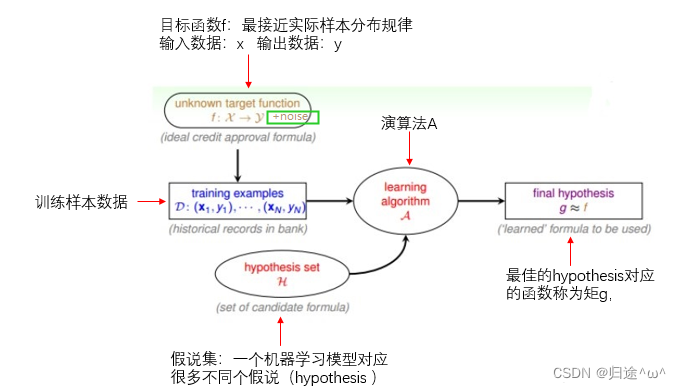
2.Pocket Algorithm的思想
1).语言描述:
首先初始化权重w0,计算出在这条初始化的直线中,分类错误点的个数,然后对错误点进行矫正,更新w,得到新的直线,再计算分类错误的点的个数,并于之前错误点数进行比较,保存错误点数少的直线,迭代结束后,选取错误点数最少的直线对应的w,即为最终权重值。
2).公式描述:

3).何判断数据集D是不是线性可分的方法
对二维数据来说,通常还是通过肉眼观察来判断的。一般情况下,Pocket Algorithm要比PLA速度慢一些,因为Pocket Algorithm每次都需要收集错误点数并于之前的数据进行比较,看哪条分类直线错误点数更少。
2.5 总结
本章主要介绍了常用的机器学习模型——感知机,解决线性分类问题的PLA算法以及解决非线性问题的Pocket Algorithm算法(PLA的修改版本)。



![Java并发体系-锁与同步-[1]](https://img-blog.csdnimg.cn/8d410fe9f73248489e96496cebed2d2d.png)