前言

在常规卷积的过程中找到相关性低的一部分卷积核，利用这部分卷积核结合深度可分离卷积搭建起新的网络框架。

一、协方差判断卷积核相关性

协方差是对应两样本并评估之间的相关程度的, 样本协方差的定义为

$$Cov(X,Y)=\frac{1}{n-1}\sum _{i=1}^n(x_i-\bar{x})(y_i-\bar{y})$$

其中 X,Y 表示两个不同的样本空间。

问题一: 不同的样本空间？

从统计和概率学的角度出发，协方差是判断两个维度的随机变量的相关性。比如身高和体重之间的关系或者地区居住人口和地区人均收入之间的关系。其中身高和体重是不同的样本空间，地区居住人口和地区人均收入是不同的样本空间。

不同的卷积核只能算做是同一个样本空间的不同样本。

问题二：计算方式？

协方差有正负之分，表示正相关和负相关。数值的大小表示 “相关的程度”, 这里就有一个"悖论"。

当协方差越大的时候, 表示两变量之间相关性越大。对卷积核而言，当协方差更小时就应该保留这两个卷积核，但是遇见下列情况的卷积核时，会出现一些问题。

卷积核 A

卷积核 B

卷积核 C

经过计算，应该保留的是卷积核 A 和 卷积核 B。但是 A B 两个卷积核是相同的。

想法

对卷积核降维, 使其从二维矩阵降为一维向量。然后利用余弦公式进行判断，若两向量正交则表示线性无关，可以进行保留。

二、整体流程

要通过算法来选择常规卷积的卷积核，是需要使用常规卷积训练后进行选择，还是动态地在训练过程中利用算法进行处理？

三、BSConv-核内相似性

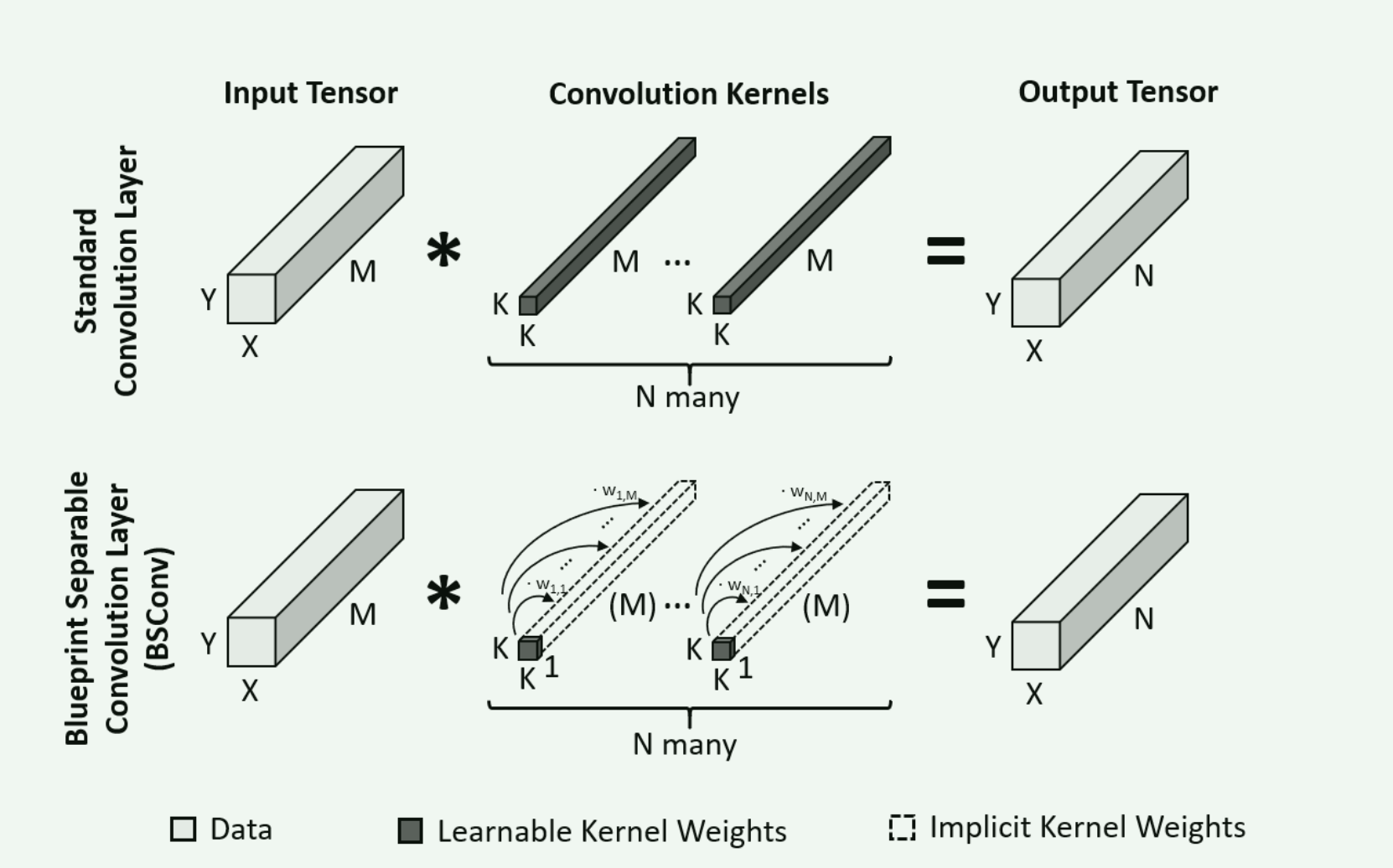
之前的 GhostNet 考虑的是核间的相似性, BSConv 考虑的是核内的相似性。

在常规卷积中, 每个卷积层对输入张量 $U\in R^{M\times Y\times X}$ 进行变化得到输出张量 $V\in R^{N\times Y\times X}$ ，相应的卷积核 $F^{(1)}$ … $F^{(N)}$, 每个卷积核的尺寸为 $M\times K\times K$。相应的公式可以描述为

V n , : , : = U ∗ F ( N ) , n ∈ { 1 , . . . , N } V_{n,:,:} = U * F^{(N)}, n \in \{1, ... , N\} Vn,:,:​=U∗F(N),n∈{1,...,N}