【追梦之旅】—— 手“C”二叉树~😎
- 前言🙌
- 什么是二叉树?!
- 特殊的二叉树
- 二叉树的性质
- 二叉树的存储结构
- 二叉树链式结构的实现
- 二叉树的链式结构:
- 二叉树的创建。
- 二叉树的遍历
- 前序遍历(先根遍历)
- 中序遍历(中根遍历)
- 后序遍历(后根遍历)
- 层序遍历
- 二叉树的经典玩法:
- 二叉树结点个数
- 二叉树叶子结点个数
- 二叉树查找值为x的节点
- 二叉树第k结点个数
- 判断二叉树是否是完全二叉树
- 总结撒花💞

😎博客昵称:博客小梦
😊最喜欢的座右铭:全神贯注的上吧!!!
😊作者简介:一名热爱C/C++,算法等技术、喜爱运动、热爱K歌、敢于追梦的小博主!
😘博主小留言:哈喽!😄各位CSDN的uu们,我是你的博客好友小梦,希望我的文章可以给您带来一定的帮助,话不多说,文章推上!欢迎大家在评论区唠嗑指正,觉得好的话别忘了一键三连哦!😘
前言🙌
哈喽各位友友们😊,我今天又学到了很多有趣的知识,现在迫不及待的想和大家分享一下!😘我仅已此文,手把手带领大家学习如何**手“C”二叉树** 都是精华内容,可不要错过哟!!!😍😍😍
什么是二叉树?!
csdn InsCodeAl的解释:二叉树是一种树形数据结构,它由一些节点和连接这些节点的边组成。每个节点最多有两个子节点,其中一个是左子节点,另一个是右子节点。节点没有子节点的被称为叶子节点。二叉树的根节点是树的顶部节点,它没有父节点。二叉树可以被用来表示表达式、文件系统、编译器语法分析树等等。
我的理解:
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
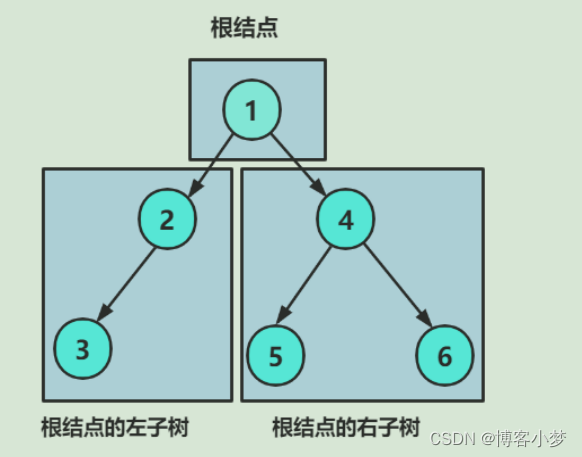
3. 二叉树不存在度大于2的结点
比特科技
4. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
5.二叉树有以下几种类型:
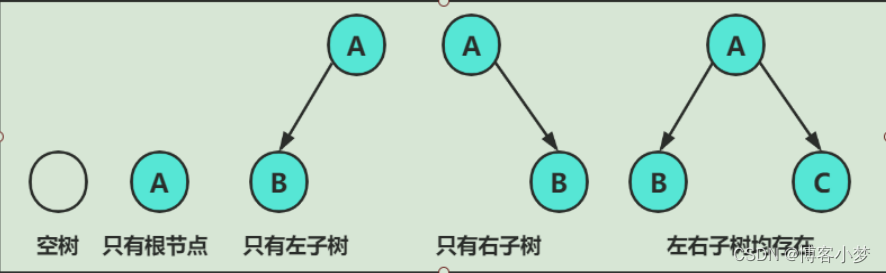
特殊的二叉树
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^k - 1 ,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。简单来说,就是左子树可以没有右子树,但是有右子树一定有左子树。要注意的是满二叉树是一种特殊的完全二叉树。
二叉树的性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 2^(i - 1)个结点.
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是 2^h - 1.
- 对任何一棵二叉树, 如果度为0其叶结点个数为N0 , 度为2的分支结点个数为N2 ,则有 N0= N2+1
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=log(n + 1) . (ps: 是log以2
为底,n+1为对数) - 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
- 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
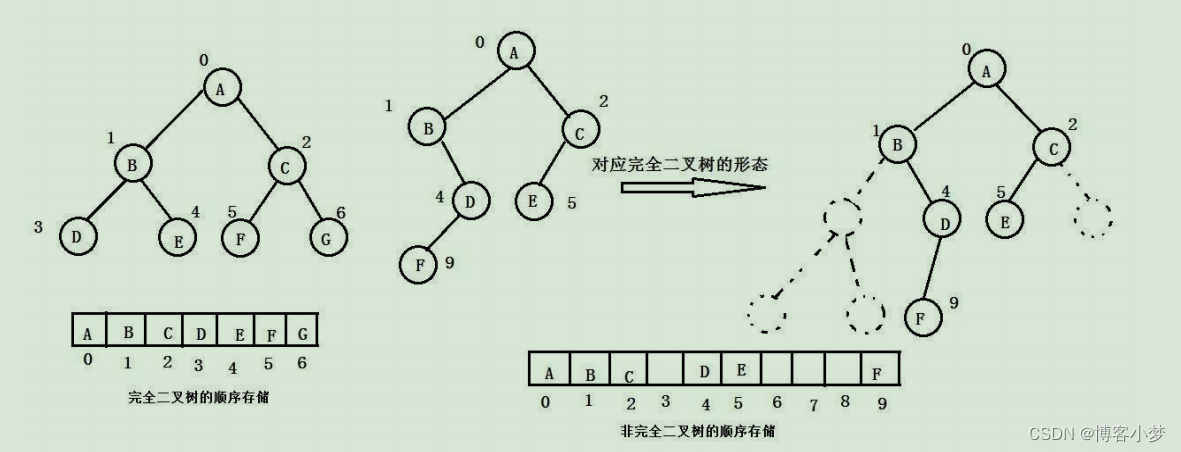
- 链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,红黑树会用到三叉链。
二叉树链式结构的实现
二叉树的链式结构:
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;
二叉树的创建。
这里利用前序遍历来创建我们的二叉树,源码如下:
BTNode* CreateNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail!\n");
return NULL;
}
newnode->_data = x;
newnode->_left = NULL;
newnode->_right = NULL;
return newnode;
}
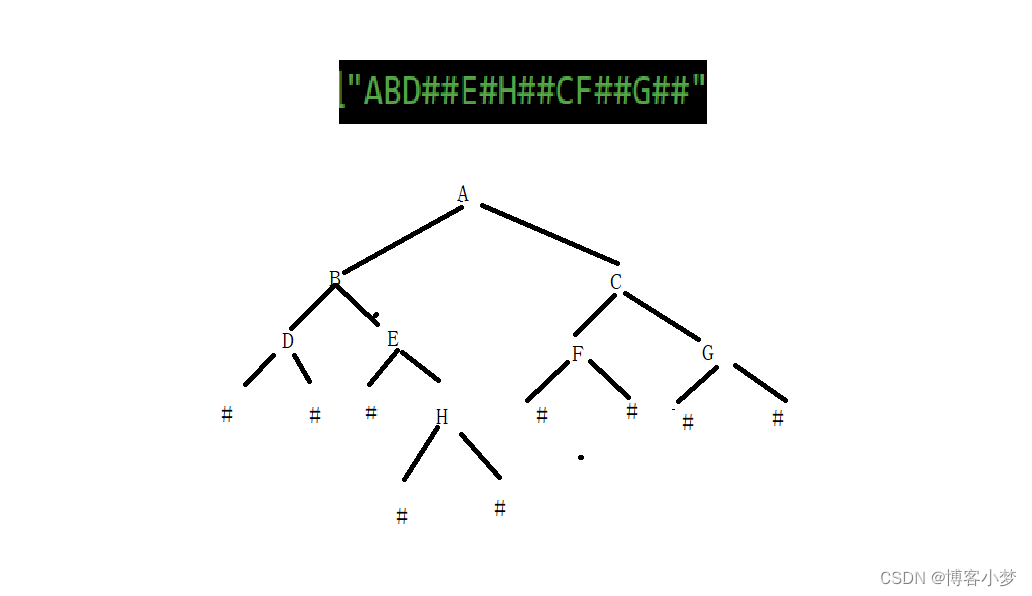
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
if (n == 0)
{
*pi = 0;
return NULL;
}
if (*a == '#')
{
*pi = 1;
return NULL;
}
int leftSize = 0;
int rightSize = 0;
BTNode* root = CreateNode(*a);
root->_left = BinaryTreeCreate(a + 1, n - 1, &leftSize);
root->_right = BinaryTreeCreate(a + 1 + leftSize, n - 1 - leftSize, &rightSize);
*pi = leftSize + rightSize + 1;
return root;
}
CreateNode函数是开辟结点的函数,利用malloc函数在堆区申请结点空间。我们在这里提供一个字符数组传递到 BinaryTreeCreate(BTDataType a, int n, int pi)函数,字符中的‘#’表示为空
该树的形状如下图所示:
二叉树的遍历
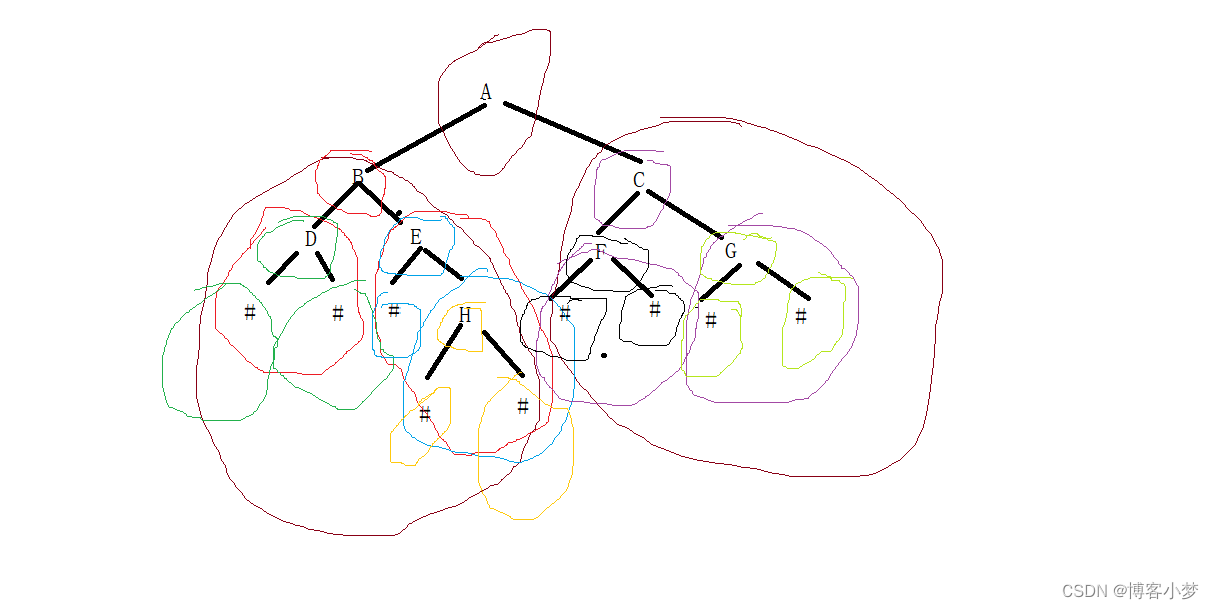
我们要把一个数递归分为根、左子树、右子树。
前序遍历(先根遍历)
遍历规律: 根 -->左子树–>右子树
源码展示:
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
printf(" # ");
return;
}
printf(" %c ", root->_data);
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
}
中序遍历(中根遍历)
遍历规律: 左子树–> 根–> 右子树
源码展示:
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
printf("#");
return;
}
BinaryTreePrevOrder(root->_left);
printf(" %c ", root->_data);
BinaryTreePrevOrder(root->_right);
}
后序遍历(后根遍历)
遍历规律: 左子树–>右子树–>根
源码展示:
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
printf("#");
return;
}
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
printf(" %c ", root->_data);
}
层序遍历
遍历规律: 从上往下,从左至右 ,一层一层遍历
这里实现的层序遍历,是利用队列数据结构来实现的。采用的算法思想是:上一层带下一层,简单的来说就是父亲带孩子。先将根节点入队列,然后出队列时将它的孩子都入队列,然后递归。当队列为空时,说明已经遍历完毕。
源码展示:
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* Front = QueueFront(&q);
QueuePop(&q);
printf(" %c ", Front->_data);
if (Front->_left)
{
QueuePush(&q, Front->_left);
}
if (Front->_right)
{
QueuePush(&q, Front->_right);
}
}
printf("\n");
QueueDestroy(&q);
}
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
if (root == NULL)
return true;
if ((root->_left == NULL) && (root->_right == NULL))
{
return true;
}
if (root->_left == NULL)
{
return false;
}
return BinaryTreeComplete(root->_left) && BinaryTreeComplete(root->_right);
}
二叉树的经典玩法:
二叉树结点个数
求解二叉树结点的个数,我们可以利用递归的思想。要想求整棵树的结点,就先求出这棵树左子树和右子树的结点个数,然后再加上自己,就是整棵树的结点个数了。
源码分享:
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
return 0;
return BinaryTreeSize(root->_left)
+ BinaryTreeSize(root->_right) + 1;
}
二叉树叶子结点个数
同样的,利用递归。将问题划分为一个一个子问题。求整棵树的叶子结点,其实就是求出其左子树 + 右子树的叶子结点。
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if ((root->_left == NULL) && (root->_right == NULL))
return 1;
return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
二叉树查找值为x的节点
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->_data == x)
return root;
BTNode* left_find = BinaryTreeFind(root->_left, x);
if (left_find != NULL)
return left_find;
BTNode* right_find = BinaryTreeFind(root->_right, x);
if (right_find != NULL)
return right_find;
return NULL;
}
二叉树第k结点个数
// 二叉树第k层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
return 0;
if (k == 1)
return 1;
return BinaryTreeLevelKSize(root->_left, k - 1)
+ BinaryTreeLevelKSize(root->_right, k - 1);
}
判断二叉树是否是完全二叉树
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
if (root == NULL)
return true;
if ((root->_left == NULL) && (root->_right == NULL))
{
return true;
}
if (root->_left == NULL)
{
return false;
}
return BinaryTreeComplete(root->_left) && BinaryTreeComplete(root->_right);
}
运行结果截图:
这是我们的二叉树:
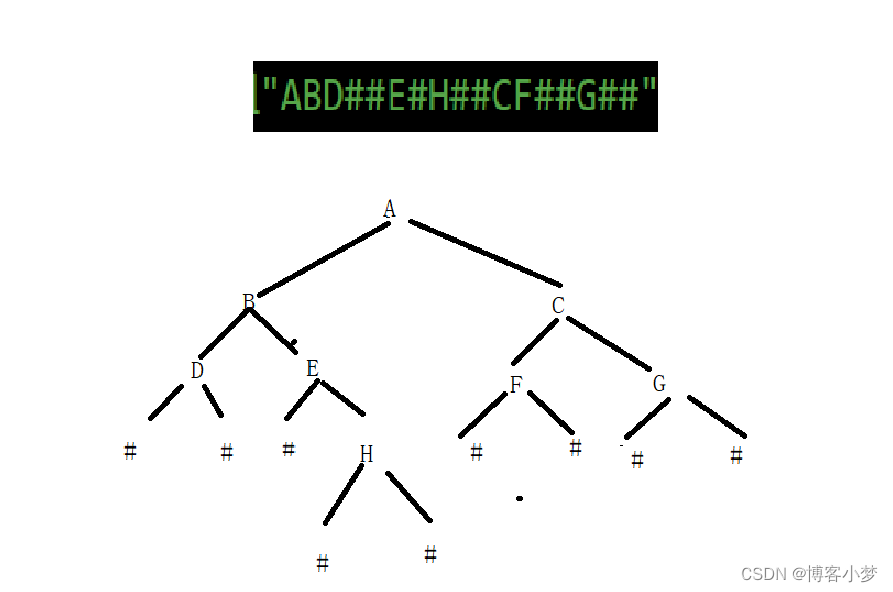

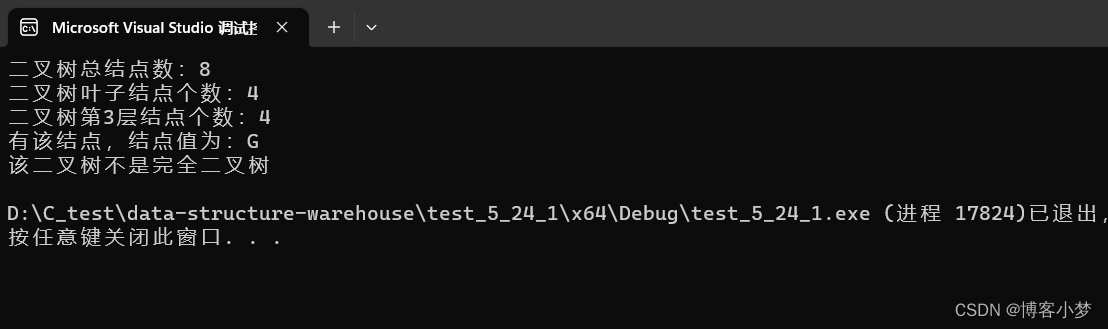
显然,我们的测试结果都是正确哒~
总结撒花💞
本篇文章旨在分享二叉树的相关知识,以及如何手“C”二叉树 。希望大家通过阅读此文有所收获!完整代码我就不发出来啦,有需要的可以私信我~
😘如果我写的有什么不好之处,请在文章下方给出你宝贵的意见😊。如果觉得我写的好的话请点个赞赞和关注哦~😘😘😘







![《汇编语言》- 读书笔记 - 第5章- [BX]和 loop 指令](https://img-blog.csdnimg.cn/16ecdcdd473e4e1cb08e1caa24a32d1c.png)