跟着九章侯老师学习了动态规划专题之后根据学习所总结：

1 题目描述

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是回文。

返回符合要求的 最少分割次数 。

2 示例

2.1 示例 1：

输入：s = “aab”
输出：1
解释：只需一次分割就可将 s 分割成 [“aa”,“b”] 这样两个回文子串。

2.2 示例 2：

输入：s = “a”
输出：0

2.3 示例 3：

输入：s = “ab”
输出：1

2.4 提示：

1 <= s.length <= 2000
s 仅由小写英文字母组成

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/palindrome-partitioning-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

3 解题思路和方法

3.1 解题思路

3.1.1 确定状态

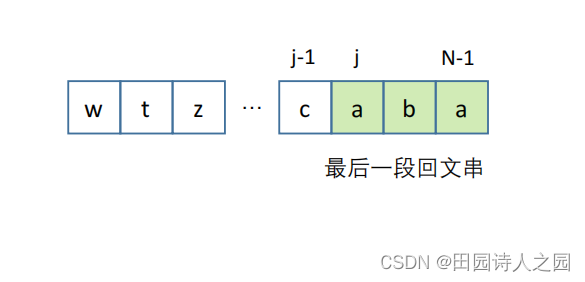
• 最后一步：关注最优策略中最后一段回文串，设为S[j…N-1];
• 需要知道S前j个字符[0…j-1]最少可以划分成几个回文串
• 子问题：
• 状态：设S前i个字符S[0…i-1]最少可以划分成f[i]个回文串
  

3.1.2 转移方程

• 设S前i个字符S[0…i-1]最少可以划分成f[i]个回文串
  

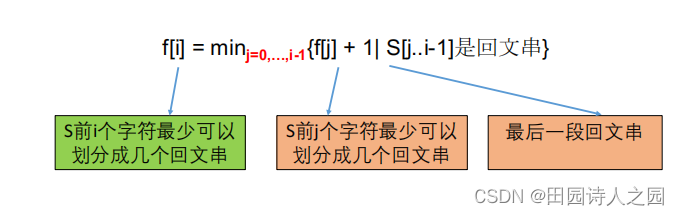
3.1.3 初始条件和边界情况

• 设S前i个字符S[0…i-1]最少可以划分成f[i]个回文串
• 初始化条件：空串可以被分成0个回文串 f[0] = 0

3.1.4 计算顺序

计算f[0],f[1],f[2],…,f[N]

3.1.5 回文串的判断方法

根据奇和偶数回文串的特点采用下面的方式去处理

3.2 算法代码实现

• 首先判断回文串

   for (int i = n - 1; i >= 0; --i) {
        for (int j = i + 1; j < n; ++j) {
            g[i][j] = (s[i] == s[j]) && g[i + 1][j - 1];
        }
    }

• 根据遍历的字符串是否为回文串计算最少划分次数

for (int j = 0; j < i; ++j) {
                if (g[j + 1][i]) {
                    f[i] = fmin(f[i], f[j] + 1);
                }
            }

最终算法代码实现如下所示：

int minCut(char* s) {
    int n = strlen(s);
    bool g[n][n];
    memset(g, 1, sizeof(g));

    for (int i = n - 1; i >= 0; --i) {
        for (int j = i + 1; j < n; ++j) {
            g[i][j] = (s[i] == s[j]) && g[i + 1][j - 1];
        }
    }

    int f[n];
    for (int i = 0; i < n; ++i) {
        f[i] = INT_MAX;
    }
    for (int i = 0; i < n; ++i) {
        if (g[0][i]) {
            f[i] = 0;
        } else {
            for (int j = 0; j < i; ++j) {
                if (g[j + 1][i]) {
                    f[i] = fmin(f[i], f[j] + 1);
                }
            }
        }
    }

    return f[n - 1];
}