Python论文复现：《基于稀疏指标的优化变分模态分解方法》
信号分解方法中，虽然变分模态分解（Variational Mode Decomposition, VMD）有严格的数学推导，能有效抑制端点效应、模态混叠等问题，但其分解模态数需预设。然而实际工程中，真实信号的频谱较为嘈杂且频带个数较难确定，一般观察分析具体信号的频谱图设置合理的模态数。
相比人工选取方法，自适应选取方法通常定义分解好坏的指标，进一步确定该指标下的最佳模态数。考虑到《基于稀疏指标的优化变分模态分解方法》从IMF频带稀疏性（VMD分解的初衷）的角度寻优，且稀疏指标有严格的理论支撑《信号的稀疏性分析》，故本文对其进行复现。
vmd分解
VMD 假定所有分量都是集中在各自中心频率附近的窄带信号，根据分量窄带条件建立约束优化问题，从而估计信号分量的中心频率以及重构相应分量。具体原理不再赘述，由于之前有粉丝不知道我用的什么代码，故在此公开，可单独放在vmdpy.py文件，后面的主程序Auto_VMD.py会调用：
import numpy as np
def VMD(f, alpha, tau, K, DC, init, tol):
"""
u,u_hat,omega = VMD(f, alpha, tau, K, DC, init, tol)
Variational mode decomposition
Python implementation by Vinícius Rezende Carvalho - vrcarva@gmail.com
code based on Dominique Zosso's MATLAB code, available at:
https://www.mathworks.com/matlabcentral/fileexchange/44765-variational-mode-decomposition
Original paper:
Dragomiretskiy, K. and Zosso, D. (2014) ‘Variational Mode Decomposition’,
IEEE Transactions on Signal Processing, 62(3), pp. 531–544. doi: 10.1109/TSP.2013.2288675.
Input and Parameters:
---------------------
f - the time domain signal (1D) to be decomposed
alpha - the balancing parameter of the data-fidelity constraint
tau - time-step of the dual ascent ( pick 0 for noise-slack )
K - the number of modes to be recovered
DC - true if the first mode is put and kept at DC (0-freq)
init - 0 = all omegas start at 0
1 = all omegas start uniformly distributed
2 = all omegas initialized randomly
tol - tolerance of convergence criterion; typically around 1e-6
Output:
-------
u - the collection of decomposed modes
u_hat - spectra of the modes
omega - estimated mode center-frequencies
"""
if len(f)%2:
f = f[:-1]
# Period and sampling frequency of input signal
fs = 1./len(f)
ltemp = len(f)//2
fMirr = np.append(np.flip(f[:ltemp],axis = 0),f)
fMirr = np.append(fMirr,np.flip(f[-ltemp:],axis = 0))
# Time Domain 0 to T (of mirrored signal)
T = len(fMirr)
t = np.arange(1,T+1)/T
# Spectral Domain discretization
freqs = t-0.5-(1/T)
# Maximum number of iterations (if not converged yet, then it won't anyway)
Niter = 500
# For future generalizations: individual alpha for each mode
Alpha = alpha*np.ones(K)
# Construct and center f_hat
f_hat = np.fft.fftshift((np.fft.fft(fMirr)))
f_hat_plus = np.copy(f_hat) #copy f_hat
f_hat_plus[:T//2] = 0
# Initialization of omega_k
omega_plus = np.zeros([Niter, K])
if init == 1:
for i in range(K):
omega_plus[0,i] = (0.5/K)*(i)
elif init == 2:
omega_plus[0,:] = np.sort(np.exp(np.log(fs) + (np.log(0.5)-np.log(fs))*np.random.rand(1,K)))
else:
omega_plus[0,:] = 0
# if DC mode imposed, set its omega to 0
if DC:
omega_plus[0,0] = 0
# start with empty dual variables
lambda_hat = np.zeros([Niter, len(freqs)], dtype = complex)
# other inits
uDiff = tol+np.spacing(1) # update step
n = 0 # loop counter
sum_uk = 0 # accumulator
# matrix keeping track of every iterant // could be discarded for mem
u_hat_plus = np.zeros([Niter, len(freqs), K],dtype=complex)
#*** Main loop for iterative updates***
while ( uDiff > tol and n < Niter-1 ): # not converged and below iterations limit
# update first mode accumulator
k = 0
sum_uk = u_hat_plus[n,:,K-1] + sum_uk - u_hat_plus[n,:,0]
# update spectrum of first mode through Wiener filter of residuals
u_hat_plus[n+1,:,k] = (f_hat_plus - sum_uk - lambda_hat[n,:]/2)/(1.+Alpha[k]*(freqs - omega_plus[n,k])**2)
# update first omega if not held at 0
if not(DC):
omega_plus[n+1,k] = np.dot(freqs[T//2:T],(abs(u_hat_plus[n+1, T//2:T, k])**2))/np.sum(abs(u_hat_plus[n+1,T//2:T,k])**2)
# update of any other mode
for k in np.arange(1,K):
#accumulator
sum_uk = u_hat_plus[n+1,:,k-1] + sum_uk - u_hat_plus[n,:,k]
# mode spectrum
u_hat_plus[n+1,:,k] = (f_hat_plus - sum_uk - lambda_hat[n,:]/2)/(1+Alpha[k]*(freqs - omega_plus[n,k])**2)
# center frequencies
omega_plus[n+1,k] = np.dot(freqs[T//2:T],(abs(u_hat_plus[n+1, T//2:T, k])**2))/np.sum(abs(u_hat_plus[n+1,T//2:T,k])**2)
# Dual ascent
lambda_hat[n+1,:] = lambda_hat[n,:] + tau*(np.sum(u_hat_plus[n+1,:,:],axis = 1) - f_hat_plus)
# loop counter
n = n+1
# converged yet?
uDiff = np.spacing(1)
for i in range(K):
uDiff = uDiff + (1/T)*np.dot((u_hat_plus[n,:,i]-u_hat_plus[n-1,:,i]),np.conj((u_hat_plus[n,:,i]-u_hat_plus[n-1,:,i])))
uDiff = np.abs(uDiff)
#Postprocessing and cleanup
#discard empty space if converged early
Niter = np.min([Niter,n])
omega = omega_plus[:Niter,:]
idxs = np.flip(np.arange(1,T//2+1),axis = 0)
# Signal reconstruction
u_hat = np.zeros([T, K],dtype = complex)
u_hat[T//2:T,:] = u_hat_plus[Niter-1,T//2:T,:]
u_hat[idxs,:] = np.conj(u_hat_plus[Niter-1,T//2:T,:])
u_hat[0,:] = np.conj(u_hat[-1,:])
u = np.zeros([K,len(t)])
for k in range(K):
u[k,:] = np.real(np.fft.ifft(np.fft.ifftshift(u_hat[:,k])))
# remove mirror part
u = u[:,T//4:3*T//4]
# recompute spectrum
u_hat = np.zeros([u.shape[1],K],dtype = complex)
for k in range(K):
u_hat[:,k]=np.fft.fftshift(np.fft.fft(u[k,:]))
return u, u_hat, omega
边际谱
论文作者是在每个IMF的边际谱上计算稀疏化指标，而边际谱是希尔伯特谱在时间维度上的积分。笔者首先将求边际谱的代码函数化，由于需要进行希尔伯特变换，本代码需要调用PyEMD与scipy库。
h
(
z
)
=
∫
0
T
H
(
t
,
f
)
d
t
h(z) = \int_0^T H(t,f)dt\
h(z)=∫0TH(t,f)dt
from PyEMD import Visualisation
from scipy.signal import hilbert
#求窄带信号的边际谱
def mspect(Fs,signal,draw=1):
fmin,fmax=0,Fs/2
size=len(signal)//2
df=(fmax-fmin)/(size-1)
t=np.arange(0,len(signal)/Fs,1/Fs)
vis = Visualisation()
#希尔伯特变化
signal=signal.reshape(1,-1)
#求瞬时频率
freqs = abs(vis._calc_inst_freq(signal, t, order=False, alpha=None))
#求瞬时幅值
amp= abs(hilbert(signal))
#去掉为1的维度
freqs=np.squeeze(freqs)
amp=np.squeeze(amp)
result=np.zeros(size)
for i,j in zip(freqs,amp):
if i>=fmin and i<=fmax:
result[round((i-fmin)/df)]+=j
f=np.arange(fmin,size*df,df)
#可视化
if draw==1: #可视化
plt.figure()
plt.rcParams['font.sans-serif']='Times New Roman'
plt.plot(f,result)
plt.xlabel('f/HZ',fontsize=16)
plt.ylabel('amplitude',fontsize=16)
plt.title('Marginal Spectrum',fontsize=20)
return f,result
基于稀疏指标自适应寻找最佳分解K值
总结论文思路如下：
1）初始化VMD参数，惩罚因子
α
\alpha
α为3000，拉格朗日乘子更新因子为0.01，分解模态数K为2；
2）VMD分解并计算各IMF的边际谱，计算各IMF的稀疏度（考虑了能量权值因子）；
S i = max { M S i } max { max { M S 1 } ⋯ max { M S k } } { E ( M S i 2 ) / [ E ( M S i ) ] 2 } {S}_{i}=\frac{\max \left\{ M{{S}_{i}} \right\}}{\max \left\{ \max \left\{ M{{S}_{1}} \right\}\cdots \max \left\{ M{{S}_{k}} \right\} \right\}}\left\{ E(MS_{i}^{2})/{{\left[ E(M{{S}_{i}}) \right]}^{2}} \right\} Si=max{max{MS1}⋯max{MSk}}max{MSi}{E(MSi2)/[E(MSi)]2}
3）取各IMF边际谱稀疏度作为该分解模态数K下的整体稀疏度；
S K = 1 K ∑ i = 1 K S i {{S}_{K}}=\frac{1}{K}\sum\limits_{i=1}^{K}{{{S}_{i}}} SK=K1i=1∑KSi
4）当
S
K
<
S
K
−
1
(
K
>
2
)
{{S}_{K}}<{{S}_{K-1}}(K>2)
SK<SK−1(K>2)时，选取最佳分解模态数为K-1，进入步骤5），反之令
K
=
K
+
1
K=K+1
K=K+1回到步骤2）继续迭代；
5）采用最佳的分解模态数进行VMD分解。
该文在确定最佳分解模态数时是选取第一个极大值点，或者稀疏度随K单调递减时，选取第一个点2。然而，实际信号极值点可能不为最大值点，且若出现先递减后递增（稀疏度大于K=2）的情况时，该方法无法取到最佳K值。
本人对选取方法做了一点小改变，即：预设最大K值（依据信号复杂度设置，本人取10），计算K从2至最大值期间的稀疏度，取最大稀疏度对应的K值作为最佳分解模态数。主函数Auto_VMD.py具体代码如下（画时频图的代码，我之前的博文有）：
from vmdpy import VMD
import matplotlib.pyplot as plt
import numpy as np
from PyEMD import Visualisation
from scipy.signal import hilbert
#求窄带信号的边际谱
def mspect(Fs,signal,draw=1):
fmin,fmax=0,Fs/2
size=len(signal)//2
df=(fmax-fmin)/(size-1)
t=np.arange(0,len(signal)/Fs,1/Fs)
vis = Visualisation()
#希尔伯特变化
signal=signal.reshape(1,-1)
#求瞬时频率
freqs = abs(vis._calc_inst_freq(signal, t, order=False, alpha=None))
#求瞬时幅值
amp= abs(hilbert(signal))
#去掉为1的维度
freqs=np.squeeze(freqs)
amp=np.squeeze(amp)
result=np.zeros(size)
for i,j in zip(freqs,amp):
if i>=fmin and i<=fmax:
result[round((i-fmin)/df)]+=j
f=np.arange(fmin,size*df,df)
#可视化
if draw==1: #可视化
plt.figure()
plt.rcParams['font.sans-serif']='Times New Roman'
plt.plot(f,result)
plt.xlabel('f/HZ',fontsize=16)
plt.ylabel('amplitude',fontsize=16)
plt.title('Marginal Spectrum',fontsize=20)
return f,result
#基于稀疏指标自适应确定K值的VMD分解
def Auto_VMD_main(signal,Fs,draw=1,maxK=10):
#vmd参数设置
alpha = 3000 # moderate bandwidth constraint 2000
tau = 0. # noise-tolerance (no strict fidelity enforcement)
DC = 0 # no DC part imposed
init = 1 # initialize omegas uniformly
tol = 1e-7
#寻找最佳K
S=[[],[]]
flag,idx=-2,2
for K in range(2,maxK+1):
IMFs,_,_=VMD(signal, alpha, tau, K, DC, init, tol) #分解信号
M_spect=[]
max_M=[]
for i in range(len(IMFs)):
# _,_=fftlw(Fs,IMFs[i,:],1)
_,M=mspect(Fs,IMFs[i,:],0)
max_M.append(max(M))
temp=np.mean(M**2)/(np.mean(M)**2)
M_spect.append(temp)
max_M=max_M/max(max_M)
S_index=np.mean(max_M*M_spect)
if S_index>flag:
flag=S_index
idx=K
S[0].append(K)
S[1].append(S_index)
#用最佳K值分解信号
IMFs, _, _ = VMD(signal, alpha, tau, idx, DC, init, tol)
#可视化寻优过程与最终结果
if draw==1:
plt.figure()
plt.rcParams['font.sans-serif']='Times New Roman'
plt.plot(S[0],S[1])
plt.scatter([idx],[flag],c='r',marker='*')
plt.xlabel('K',fontsize=16)
plt.ylabel('Sparse index',fontsize=16)
plt.title('Optimization Process',fontsize=20)
plt.figure()
for i in range(len(IMFs)):
plt.subplot(len(IMFs),1,i+1)
plt.plot(t,IMFs[i])
if i==0:
plt.rcParams['font.sans-serif']='Times New Roman'
plt.title('Decomposition Signal',fontsize=14)
elif i==len(IMFs)-1:
plt.rcParams['font.sans-serif']='Times New Roman'
plt.xlabel('Time/s')
return IMFs
if __name__=='__main__':
#仿真信号1
Fs=6000 #采样频率
t = np.arange(0, 1.0, 1.0 / Fs)
signal=np.multiply(np.sin(2*np.pi*100*t),(np.cos(2*np.pi*1000*t)+np.cos(2*np.pi*1500*t)+np.cos(2*np.pi*2000*t)))
# #仿真信号2
# Fs=1000 #采样频率
# t = np.arange(0, 1.0, 1.0 / Fs)
# f1,f2,f3 = 100,200,300
# signal = np.piecewise(t, [t < 1, t < 0.6, t < 0.3],
# [lambda t: np.sin(2 * np.pi * f1 * t), lambda t: np.sin(2 * np.pi * f2 * t),
# lambda t: np.sin(2 * np.pi * f3 * t)])
# #仿真信号3
# Fs=1000 #采样频率
# t = np.arange(0, 1.0, 1.0 / Fs)
# f1,f2,f3 = 100,200,300
# signal = 3*np.sin(2*np.pi*f1*t)+6*np.sin(2*np.pi*f2*t)+5*np.sin(2*np.pi*f3*t)
IMFs=Auto_VMD_main(signal,Fs,draw=1,maxK=10)
from eemd_hht import hhtlw
tt,ff,c_matrix=hhtlw(IMFs,t,f_range=[0,Fs/2],t_range=[0,t[-1]],ft_size=[128,128]) #画希尔伯特谱
仿真信号分析
仿真如下信号验证，采样频率为6000 Hz，信号时间长度为1 s：
y = sin ( 2 π f 1 t ) ∗ [ cos ( 2 π f 2 t ) + cos ( 2 π f 3 t ) + cos ( 2 π f 4 t ) ] y=\sin \left( 2\pi {{f}_{1}}t \right)*\left[ \cos \left( 2\pi {{f}_{2}}t \right)+\cos \left( 2\pi {{f}_{3}}t \right)+\cos \left( 2\pi {{f}_{4}}t \right) \right] y=sin(2πf1t)∗[cos(2πf2t)+cos(2πf3t)+cos(2πf4t)]
f
1
,
f
2
,
f
3
,
f
4
=
100
,
1000
,
1500
,
2000
{{f}_{1}},{{f}_{2}},{{f}_{3}},{{f}_{4}}=100,1000,1500,2000
f1,f2,f3,f4=100,1000,1500,2000
由于傅里叶变化的思想是采用标准正弦波来拟合信号，而本文信号由于出现正弦波相乘，经过三角函数积化和差可转换为6个正弦波，故原始信号频谱包含6个频率成分。
y
=
1
2
sin
(
2
π
(
f
1
+
f
2
)
t
)
+
sin
(
2
π
(
f
1
−
f
2
)
t
)
+
sin
(
2
π
(
f
1
+
f
3
)
t
)
+
y=\frac{1}{2}\sin \left( 2\pi \left( {{f}_{1}}+{{f}_{2}} \right)t \right)+\sin \left( 2\pi \left( {{f}_{1}}-{{f}_{2}} \right)t \right)+\sin \left( 2\pi \left( {{f}_{1}}+{{f}_{3}} \right)t \right)+
y=21sin(2π(f1+f2)t)+sin(2π(f1−f2)t)+sin(2π(f1+f3)t)+
sin
(
2
π
(
f
1
−
f
3
)
t
)
+
sin
(
2
π
(
f
1
+
f
4
)
t
)
+
sin
(
2
π
(
f
1
−
f
4
)
t
)
\sin \left( 2\pi \left( {{f}_{1}}-{{f}_{3}} \right)t \right)+\sin \left( 2\pi \left( {{f}_{1}}+{{f}_{4}} \right)t \right)+\sin \left( 2\pi \left( {{f}_{1}}-{{f}_{4}} \right)t \right)
sin(2π(f1−f3)t)+sin(2π(f1+f4)t)+sin(2π(f1−f4)t)
原始信号的时域图与频谱图如下：
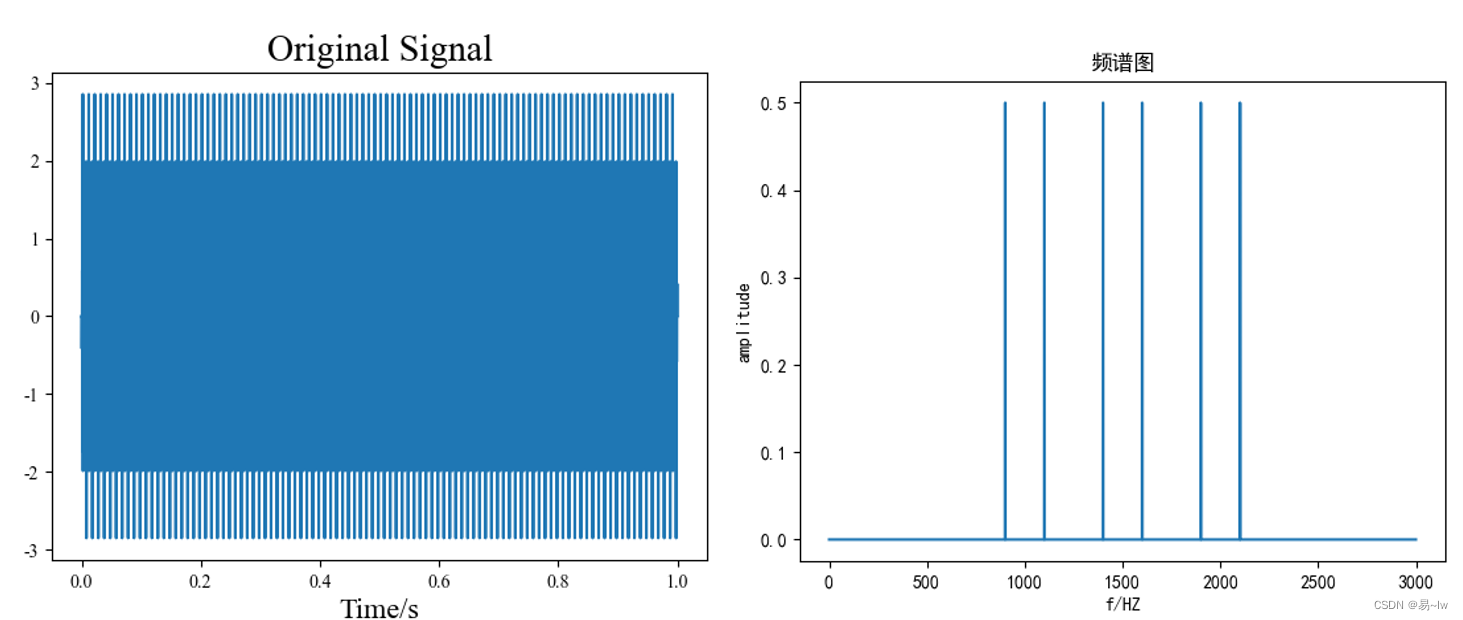
采用稀疏度自动寻找最佳K值为6，寻优过程以及分解后的时频图如下：
转子试验台数据分析
采用转子试验台数据（无故障状态）分析，采样频率为30720 Hz，样本长度为1024，原始时域及频域图如下，大致可以分为6-8个频带，图中圈圈为本方法确定的最佳模态分量数下各IMF的频带中心，基本符合信号包含的窄带个数：
采用稀疏度自动寻找最佳K值为6，寻优过程以及分解后的时频图如下：
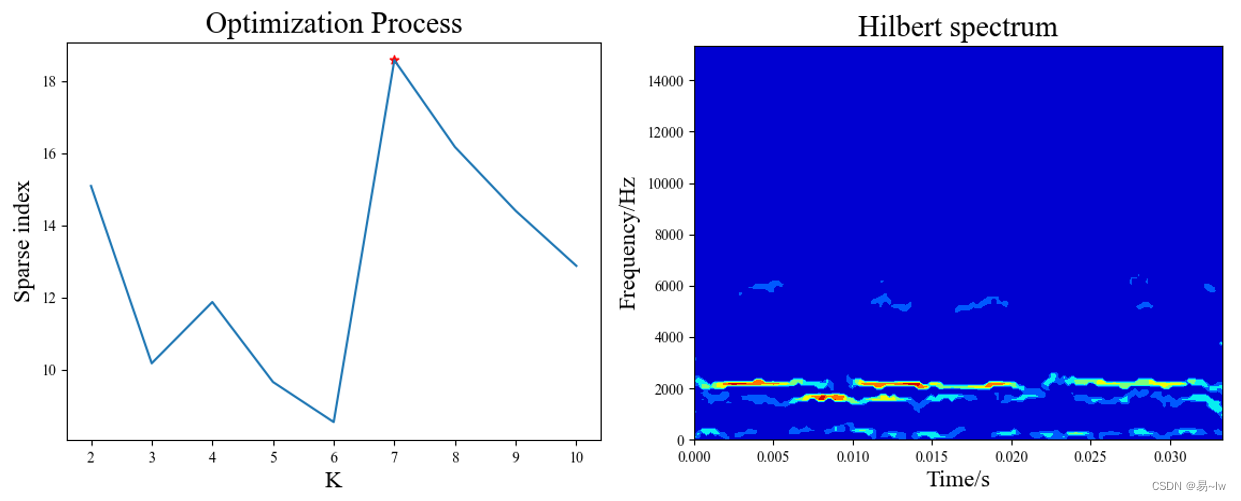各IMF的边际谱如下，基本对应频谱中的各频率成分：
