💓博主CSDN主页:杭电码农-NEO💓
 
⏩专栏分类:数据结构学习分享⏪
 
🚚代码仓库:NEO的学习日记🚚
 
🌹关注我🫵带你了解更多数据结构的知识
  🔝🔝

---

---

1. 前言

在学习链式二叉树之前,大家一定要对函数栈帧的建立与销毁有一定的了解,因为链式二叉树这一块会涉及很多递归的问题,递归会不断建立栈帧,再不断销毁.理解了函数的栈帧的建立与销毁可以帮助我们理解二叉树的内容如果你对函数栈帧没有概念,请跳转函数栈帧的创建与销毁

其实普通的二叉树的增删查改没有什么意义,因为二叉树用来存储数据太复杂了,我们一般在它的基础上增加一些性质才有意义,比如说很经典点的搜索二叉树等

注:二叉树的内容开始真正上强度了!

---

2. 链式二叉树的结构

我们之前说过,特殊的二叉树,比如完全二叉树(堆)非常适合用数组的形式来表示,而普通的二叉树就非常适合用链式结构来表示:

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>//链式二叉树

typedef char BTDataType;

typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;

这里我们直接定义一个链式结构,里面有两个指针分别指向节点的左孩子和右孩子,data用来存储值

---

当然定义完二叉树的结构后,我们还应该将它初始化指向和初始化赋值以便于我们后面使用,这里我们定义一个下图一样的二叉树:

---

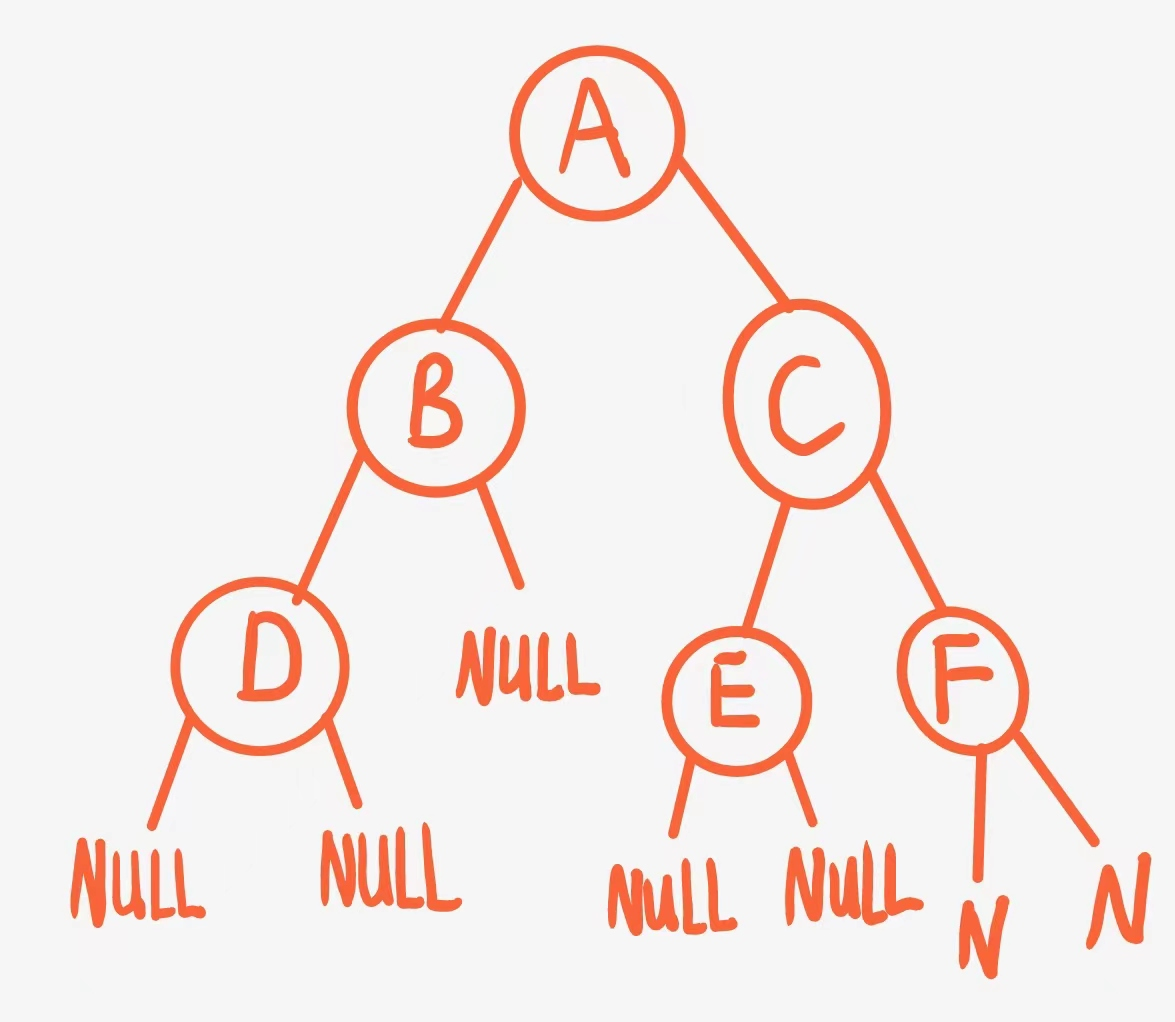
这里我们初始化节点的时候应该先将左右孩子指针都给置空,把所有节点初始化完成后再根据需要将节点链接起来:这里我们需要两个函数:

BTNode* BuyNode(BTDataType x)//这个函数用于为新节点开辟空间并且初始化
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	newnode->data = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}

上面这个函数用于为节点开辟空间并且初始化内容

BTNode* CreatBinaryTree()//手动创建一共二叉树
{
	BTNode* nodeA = BuyNode('A');
	BTNode* nodeB = BuyNode('B');
	BTNode* nodeC = BuyNode('C');
	BTNode* nodeD = BuyNode('D');
	BTNode* nodeE = BuyNode('E');
	BTNode* nodeF = BuyNode('F');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;
	return nodeA;
}

而上面这个函数用于将初始化完成后的值修改指针指向,使他变成我们想要的二叉树.像叶子节点D,E,F在开辟空间时已经将左右孩子置空了,所以这里修改指针指向时不用再刻意置空了!

---

做好这些后,我们的二叉树结构就基本建立完成了,现在我们接着往下看.

---

3. 二叉树的遍历

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。分为:

1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

我们一一来讲解:

---

3.1 二叉树前序遍历

我们用我们上面定义的二叉树来举例子:

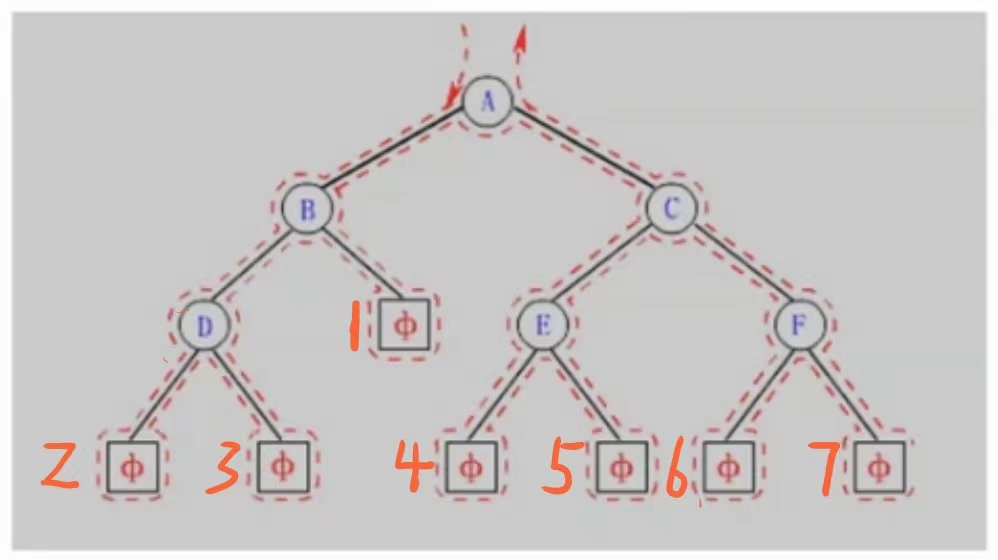
前序遍历是先访问根节点,再访问左孩子最后有孩子,我们假设将所有的NULL(空节点)编个号,这样好理解:那么对于这个二叉树的前序遍历顺序应该是:A B D 2 3 1 C E 4 5 F 6 7.将所有空节点去掉后就得到: ABDCEF.

---

3.2 前序遍历代码实现及其解释

这个代码解释起来比较费劲,这里我先给出代码,再做解释:

void PreOrder(BTNode* root)//前序遍历二叉树,递归的方法(中左右)
{
	if (root == NULL)//节点为空就打印NULL后再返回
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);//要体现出我们在遍历,这里将值打印出来
	PreOrder(root->left);
	PreOrder(root->right);
}

这里我们使用了递归的手法,前序遍历时,我们将打印内容放在最前面,然后再去递归它的左右孩子,因为这个地方不好解释,所以我建议大家自己去画图理解,这里博主把我自己画的图分享给大家:主要分为两个部分,那就是递归往后走的部分和函数调用完返回的部分

你自己画出的递归展开图其实也就是一个二叉树的形状.我们在电脑上打印出来结果,可以看见和我们之前预想的结果是相同的:

---

3.2 二叉树中序遍历

和前序一样,我们先把中序情况的顺序写出来,再来实现代码:

2 D 3 B 1 A 4 E 5 C 6 F 7.将所有空指针去掉可以得到:DBAECF

我们再来写写中序遍历的代码:

void MidOrder(BTNode* root)//中序遍历二叉树,递归(左中右)
{
	if (root == NULL)
	{
		printf("NULL");
		return;
	}
	MidOrder(root->left);
	printf("%c ", root->data);
	MidOrder(root->right);
}

是的没错!中序遍历就是在前序遍历的基础上将打印函数放在了中间位置,这很巧妙,但是你也得画图去理解,不能只是认为中序遍历就把printf放在中间! 有了前面前序遍历画图的抛砖引玉,这里的递归图就交给你们自己来画

这里还是运行结果看看能不能和我们的猜想对上

---

3.3 二叉树的后续遍历

还是老规矩,先将后续遍历的顺序给写出来: 2 3 D 1 B 4 5 E 6 7 F C A.将空指针去掉后得到: DBEFCA

和你猜想的一样,后续遍历的代码就是将printf放在最后[狗头]

void PostOrder(BTNode* root)//后续遍历二叉树(左右中)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}

到这里如果你前两个遍历都画图理解了,相信这个遍历你不画图也能参透里面的奥义了!

结果毫无疑问是能够和我们的猜想对上的:

---

4. 二叉树节点个数

二叉树节点个数我们可能会认为很简单,只需要用前序把二叉树走一步,每遇见一个非空节点就加一就可以求出节点个数,很容易写出这样的代码:

int BinaryTreeSize(BTNode* root)
{
  if(root==NULL)
  {
    return;
  }
  int count=0;

  count++;//遍历多少次非空节点就将count加几次
  BinaryTreeSize(root->left);
  BinaryTreeSize(root->right);

但是这样写有一个明显的问题,那就是count是局部变量,变量每一次调用都会创建不同的栈帧空间,也就是说每一个递归函数中的count不能被保存起来,并且我们如果在count前面加上一个static关键字将count放在静态区也是不可取的,因为当我们第一次使用我们的求二叉树节点个数的函数是没有问题的,但是当我们下一次再使用这个函数时,count值不是从0开始,而是从6开始(二叉树有六个元素),第三次调用count就从12开始. 所以这里我们修改一下代码:

void BinaryTreeSize(BTNode* root, int* p)//二叉树节点的个数,这里的p是外面main定义的变量的地址
{
	if (root == NULL)
	{
		return;
	}
	++(*p);
	BinaryTreeSize(root->left,p);
	BinaryTreeSize(root->right, p);
}

这里我们在外部定义一个变量来存储二叉树节点的个数,然后我们把变量的地址传进来就可以很好的修正刚刚的问题,这里还有一种写法,这种写法应该首先掌握:

int BinaryTreeSize2(BTNode* root)//求二叉树节点个数,直接返回节点个数
{
	return root == NULL ? 0 :
		BinaryTreeSize2(root->left) 
		+ BinaryTreeSize2(root->right) + 1;
}

这里如果节点为空就返回0,不为空就接着往后递归,代码比较抽象,还是需要我们画图来理解:

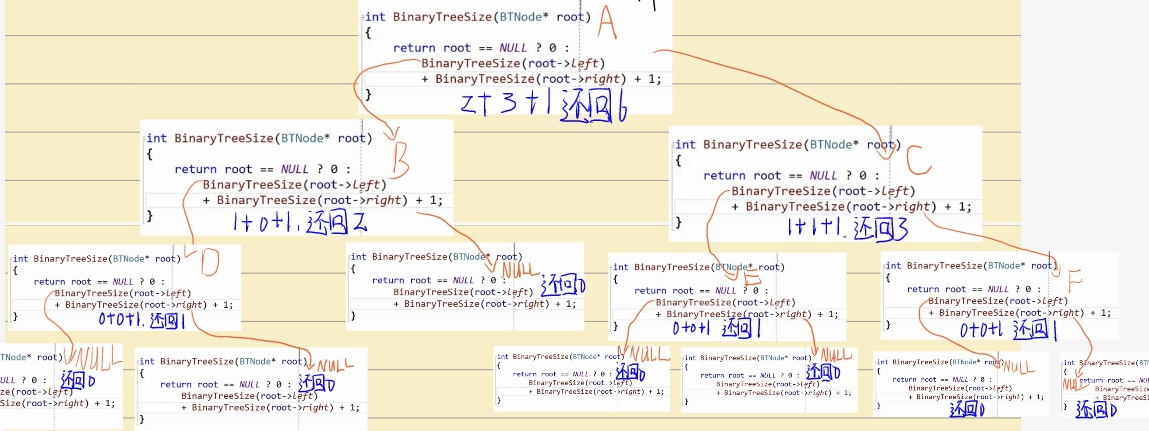
你们应该自己画图理解一番.

---

5. 二叉树叶子节点的个数

叶子节点就是左右孩子都为空的节点,首先第一步我们要想到的是,如果数为空,那么我们应该返回0因为它一个节点都没有,第二点是节点的左孩子和右孩子都为空时,我们应该返回1.当我们走完这两种情况后,剩下的情况一定是节点即不为空,并且左右孩子都不全为空,这种情况我们就再往后递归左右子树就可以了

int BinaryTreeLeafSize(BTNode* root)//求二叉树叶子节点个数(左右孩子都为空的节点)
{
	if (root == NULL)//二叉树为空的情况和遇见空节点的情况
	{
		return 0;
	}

	if (root->left == NULL && root->right == NULL)//为叶子时
	{
		return 1;
	}

	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
	//既不是叶子也不是空就返回左右节点的叶子数
}

这里值得注意的是第一步,root==NULL时,这时其实有两种情况,一种是我们数本身就是空树,第二种是我们的节点是空节点,这两种情况都应该返回0,并且其实这两种情况可以合并为一种情况

这里的递归不难理解,所以就不给大家画递归展开图了(如果你感到困难,也应该自己画一幅图)

---

6. 二叉树第K层的节点个数

我们还是可以像刚刚一样分析,当数为空树时,我们应该返回0,而这里当K等于1时,也就是第一层,一定为1个节点,所以返回1.当这两种情况都不满足时,那么说明root这棵树的第k层节点在子树里面,这样就可以转换成求左右子树的k-1层的节点个数!

int BinaryTreeLeaveSize(BTNode* root, int k)//返回二叉树第k层节点数
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	//root既不是空,k也不为1时,说明第k层在root的字树中,转换为求左右子树的第k-1层的节点树
	return BinaryTreeLeaveSize(root->left, k - 1) + BinaryTreeLeaveSize(root->right, k - 1);
}

这里只要理解了root既不是空,并且k也不等于1,我们就转换这个问题求左右子树的k-1层的节点数,再画递归展开图理解一下:

假设我们设K=3.

这里的递归用照片其实也不太好看,在这个版块大家尽量自己画图,没有画图思路的可以看看我是怎么画的,看别人的图理解起来还是很难得

---

7. 总结

二叉树的内容还没有结束,由于二叉树这一章的内容较多,我将一些内容放在下一节讲,下一节包括:求二叉树的高度,查找值为x的节点,二叉树的层序遍历,判断二叉树是不是完全二叉树.敬请期待!

🔎 下期预告:链式二叉树详解(二) 🔍

---