最大熵模型（MEMM）: 提出背景：解决模型三个缺点

最大熵结构：HMM框架加上多项的逻辑回归。

HMM缺点：

        1.观测独立假设和齐次马尔可夫假设

        解决办法：调转模型箭头

        2.模型建模和求解不一致（建模：P（X,Y）求解：（P（Y|X）））

        解决办法：生成式模型转为判别式模型，加逻辑回归

        3.不能处理复杂的问题

        解决办法：三个参数：加入复杂的特征函数

softmax（wx）=e(wx)/sum(e(wx))

每个样本都会有很多的特征，每个特征又都会有一个权重，这个权重反映的就是

特征的重要性。

特征函数：关联了y-1和xt的信息。特征函数中的东西都是自定义的。

总结：

    1.HMM的三个缺点

    2.MEMM模型概率

    3.MEMM模型图

    4.特征函数

    5.优缺点

MEMM是判别式有向图模型

CRF是判别式无向图模型

HMM（速度）CRF（精度）MEMM（速度和精度差一点）

最大熵模型（MEMM）：

首先说一下HMM的缺点：

1. 基于HMM的假设，每一个时刻的输出序列都是依靠当前的一个隐藏状态，但是在处理实际的业务的时候，有可能当前的输出序列并不仅仅依靠当前的隐藏状态，而是跟当前的隐藏状态和上一时刻的输出序列都有关系，那么这个时候HMM就做不了了。
2. HMM是生成式模型，因此是对P（X，Y）进行建模，但是对于HMM求解的问题，都是条件概率P（Y|X），因此，虽然能转换过来，但是1. 增加了无谓的计算量， 2. 构建的模型和求解的问题不匹配
3. 没有办法加入复杂的特征函数，因此在做实际场景的任务是效果比较差的，比如说命名实体识别的任务，比如一个实体标记成了B，I，O，S，而另一个是B，S对于这种不确定的规则比较复杂的，HMM不能定义出复杂的特征函数，因此效果差，同时隐马比较适用于小量的数据集合，如果在大量的数据集合上，特征之间的交互更加的复杂，HMM是解决不了的。

最大熵马尔可夫模型（Maximum Entropy Markov Model，MEMM）的思想把HMM和最大熵结合起来，可以提取特征以泛化模型能力，结合上下文依赖，直接判别减少建模负担。

首先我们不想通过求P（X，Y）概率分布了，我们想直接求得P（Y|X）的条件概率，那么什么模型可以直接求出来这个条件概率？

逻辑回归：

 

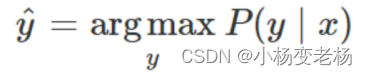
那么逻辑回归中怎么求的P（Y|X）？

将每个特征乘以一个权重，然后将它们相加，然后将指数函数应用于该线性组合：

 

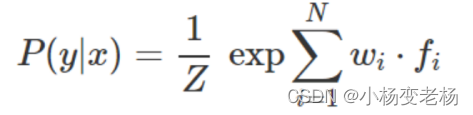
其中 fi 是一个特征，wi 是与该特征相关的权重。对于权重和特征点积进行的 exp（即，指数函数）确保所有值都是正值，并且需要除以分母 Z 以得到（所有概率值的总和为 1）有效概率。

这意味着我们将选择参数 w，使对给定输入值 x 在训练数据中 y 标签的概率最大化。我们想通过训练 logistic 回归来获得每一个特征的理想权重（使训练样本和属于的类拟合得最好的权重）。我们最想想训练的是这个权重w。

逻辑回归怎么训练的？

是不是定义通过极大似然估计，然后极大似然函数得出代价函数，计算出了代价之后，就可以进行通过梯度下降等手段进行优化和训练，

 

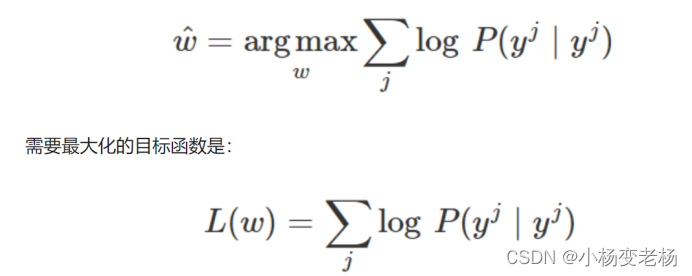
注意目标函数是不是上的公式。

因此最大熵模型的思想就是相当于：利用 HMM 框架预测给定输入序列的序列标签，同时结合多项 Logistic 回归

就是这个多项的逻辑回归给出了很大的自由度，其中输入可以包含很多不同的特征组合等等。

HMM和MEMM模型图的区别：

 

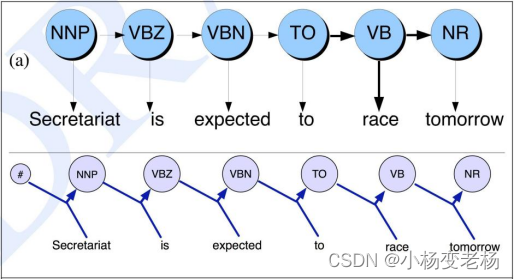
与当前输入仅依赖于当前状态的 HMM 相比，MEMM 中的当前输入也可以取决于之前的状态。HMM 模型对于每个转换和输入都有确定的概率估计，而 MEMM 给出每个隐藏状态的一个概率估计，这是给定前一个标记和输入值情况下的下一个标记的概率。

在 MEMM 不是状态转换矩阵和观测矩阵，而是只有一个转换概率矩阵。该矩阵将训练数据中先前状态 S_t-1 和当前输入 O_t 对的所有组合封装到当前状态 S_t。如果状态个数为 N，单词个数为M，那么这个矩阵的概率的大小应该为 (N⋅M)⋅N

重点：接着就是我们一直在提的特征函数：

特征函数是什么？

特征函数就是加入一些自定义的一些东西，比如：名词后边跟动词等等，也就相当于我们对游戏进行了一些规则的限定，满足的话输出就是1，不满足的话输出就是0。

对比一下逻辑回归和最大熵模型的特征函数：

·  仅仅对输入抽取特征。即特征函数为f(x)

·  对输入和输出同时抽取特征。即特征函数为f(x,y)

最终 wi 是与每个特征 fi(x,y) 相关联的需要学习的权重，也是我们要学习的目标。

最大熵模型的优点有：

最大熵统计模型获得的是所有满足约束条件的模型中信息熵极大的模型,作为经典的分类模型时准确率较高。

可以灵活地设置约束条件，通过约束条件的多少可以调节模型对未知数据的适应度和对已知数据的拟合程度

最大熵模型的缺点有：

由于约束函数数量和样本数目有关系，导致迭代过程计算量巨大，实际应用比较难。

标注问题，分类问题的对比：

首先它们都属于分类问题，而标注问题想到与是分类问题的一个拓展。都是有监督的学习，输入X，Y去计算，它们的条件概率P（Y|X），然后去确定最后类别的输出。

不同点在于：

分类问题，最后输出的是一个准确的类别，比如0，1等。而标注问题最后的输出是一个序列，一个向量，这个向量中每一个值都是标注过后的标志类型。