Problem - 1603B - Codeforces

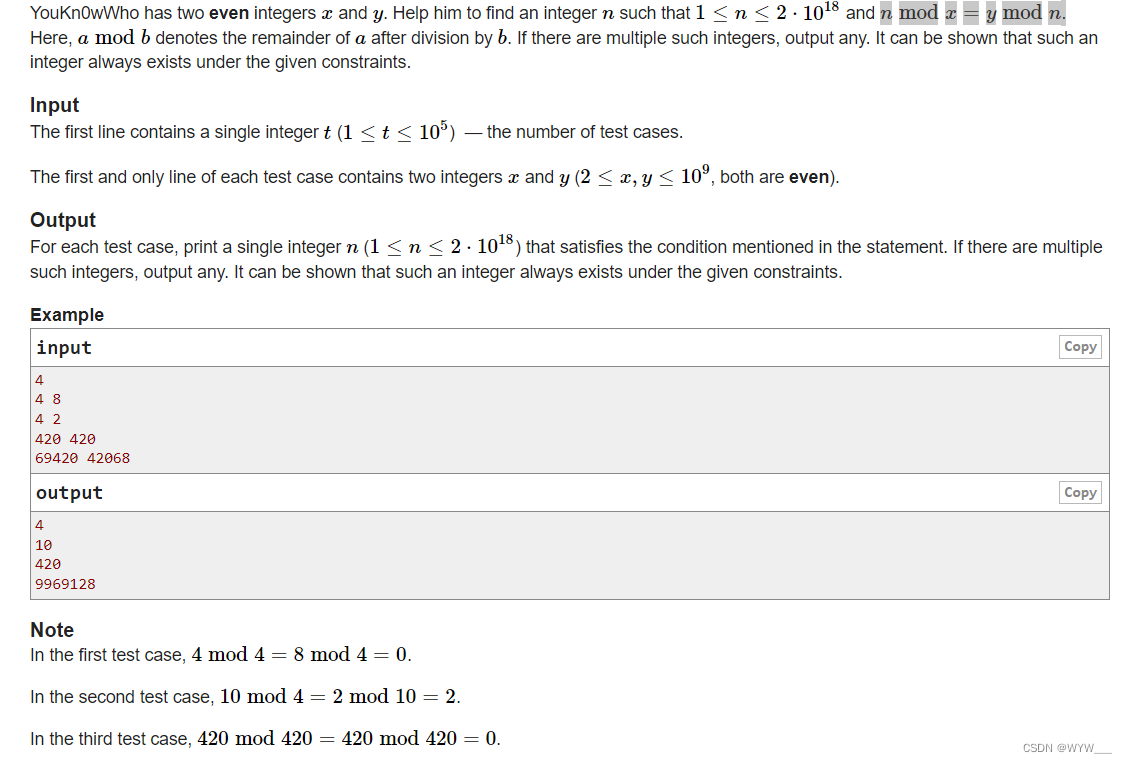
帮助他找到一个整数n，使得1≤n≤2⋅1018，并且nmodx=ymodn。这里，amodb表示a除以b后的余数。如果有多个这样的整数，请输出任何一个。可以证明，在给定的约束条件下，这样的整数总是存在的。

输入
第一行包含一个整数t（1≤t≤105）--测试案例的数量。

每个测试案例的第一行也是唯一一行包含两个整数x和y（2≤x,y≤109，都是偶数）。

输出
对于每个测试用例，打印一个满足声明中提到的条件的单个整数n（1≤n≤2⋅1018）。如果有多个这样的整数，则输出任何一个。可以证明，在给定的约束条件下，这样的整数总是存在的。

例子
输入复制
4
4 8
4 2
420 420
69420 42068
输出拷贝
4
10
420
9969128
注意
在第一个测试案例中，4mod4=8mod4=0。

在第二个测试案例中，10mod4=2mod10=2。

在第三个测试案例中，420mod420=420mod420=0。

题解:

当a > b时不难发现 答案就是 a+b

当a <= b时

1.如果n < a,n % a = n,b % n < n,所以肯定不成立

2.如果n > b,n % a < a,b % n = b,所以肯定不成立

那么答案肯定再a~b之间

假设我们设答案为k*a

那么b % k*a = b - k*a

此时左边为k*a右边为b

答案不就应该是b - k*a的中间部分吗

b - k*a = b%a

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#include<algorithm>
#include<string>
#include<map>
using namespace std;
#define int long long
char s[1000060];
void solve()
{
//	ios::sync_with_stdio(false);
//	cin.tie(0);
//	cout.tie(0);
	int n,m;
	cin >> n >>m;
	if(n == m)
	{
		cout<<n<<"\n";
	}
	else if(n > m)
	{
		cout<<n+m<<"\n";
	}
	else if(n < m)
	{
		cout <<m - m%n/2<<"\n";
	}
	
}
signed main()
{
	int t = 1;
	cin >> t;
	while(t--)
	{
		solve();
	}
}