【LetMeFly】1373.二叉搜索子树的最大键值和

力扣题目链接：https://leetcode.cn/problems/maximum-sum-bst-in-binary-tree/

给你一棵以 root 为根的 二叉树 ，请你返回任意二叉搜索子树的最大键值和。

二叉搜索树的定义如下：

任意节点的左子树中的键值都小于此节点的键值。
任意节点的右子树中的键值都大于此节点的键值。
任意节点的左子树和右子树都是二叉搜索树。

示例 1：

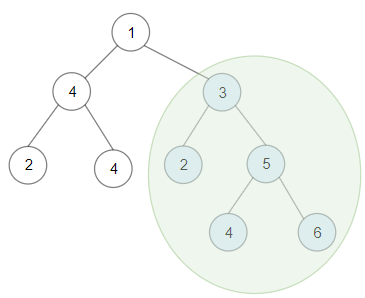
输入：root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
输出：20
解释：键值为 3 的子树是和最大的二叉搜索树。

示例 2：

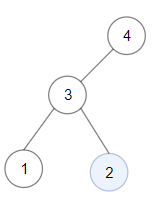
输入：root = [4,3,null,1,2]
输出：2
解释：键值为 2 的单节点子树是和最大的二叉搜索树。

示例 3：

输入：root = [-4,-2,-5]
输出：0
解释：所有节点键值都为负数，和最大的二叉搜索树为空。

示例 4：

输入：root = [2,1,3]
输出：6

示例 5：

输入：root = [5,4,8,3,null,6,3]
输出：7

提示：

每棵树有 1 到 40000 个节点。
每个节点的键值在 [-4 * 10^4 , 4 * 10^4] 之间。

方法一：深度优先搜索

定义结构体MyNode来描述子树的情况。

struct MyNode {
    int minValue;  // 子树最小值
	int maxValue;  // 子树最大值
	int sumValue;  // 子树节点和
    bool isBST;    // 子树是否为二叉搜索树
};

接着定义dfs函数来递归地判断子树。

如果当前节点为空，则认为是空的二叉搜索树。为了方便，我们将空的BST最小值定义为“无穷大”，最大值定义为“无穷小”，这样不论节点的左子为空还是右子为空，都满足左子最大值小于根，右子最小值大于根
否则，递归获取左右子树的信息。
- 如果左右子都是BST，并且满足左子最大值小于根，右子最小值大于根，那么当前节点同样是BST
- 否则，当前节点不是BST，返回的MyNode的isBST需要为false

MyNode dfs(TreeNode* root) {
	if (!root) {
		return MyNode(INT_MAX, INT_MIN, 0, true);
	}
	MyNode left = dfs(root->left);
	MyNode right = dfs(root->right);
	if (是BST) {
		构造这个节点的MyNode，返回前更新答案最大值
	}
	else {
		返回isBST为false的MyNode
	}
}

时间复杂度 $O (n)$ ，其中 $n$ 是二叉树的节点个数
空间复杂度 $O (n)$

AC代码

C++

struct MyNode {
    int minValue, maxValue, sumValue;
    bool isBST;
    MyNode(int minValue, int maxValue, int sumValue, bool isBST) : minValue(minValue), maxValue(maxValue), sumValue(sumValue), isBST(isBST) {};
};


class Solution {
private:
    int ans;

    MyNode dfs(TreeNode* root) {
        if (!root) {
            return MyNode(INT_MAX, INT_MIN, 0, true);
        }
        MyNode left = dfs(root->left), right = dfs(root->right);
        if (left.isBST && right.isBST && left.maxValue < root->val && right.minValue > root->val) {
            MyNode toReturn(min(left.minValue, root->val), max(right.maxValue, root->val), left.sumValue + right.sumValue + root->val, true);  // 这里min和max是因为left为空的话left.minValue为INT_MAX
            ans = max(ans, toReturn.sumValue);
            return toReturn;
        }
        else {
            return MyNode(0, 0, 0, false);
        }
    }
public:
    int maxSumBST(TreeNode* root) {
        ans = 0;
        dfs(root);
        return ans;
    }
};

Python

# from typing import Optional

# # Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right


class MyNode:
    def __init__(self, minValue: int, maxValue: int, sumValue: int, isBST: bool):
        self.minValue = minValue
        self.maxValue = maxValue
        self.sumValue = sumValue
        self.isBST = isBST


class Solution:
    def dfs(self, root: Optional[TreeNode]) -> MyNode:
        if not root:
            return MyNode(1e9, -1e9, 0, True)
        left = self.dfs(root.left)
        right = self.dfs(root.right)
        if left.isBST and right.isBST and left.maxValue < root.val and right.minValue > root.val:
            toReturn = MyNode(min(left.minValue, root.val), max(right.maxValue, root.val), left.sumValue + right.sumValue + root.val, True)
            self.ans = max(self.ans, toReturn.sumValue)
            return toReturn
        else:
            return MyNode(0, 0, 0, False)

    def maxSumBST(self, root: Optional[TreeNode]) -> int:
        self.ans = 0
        self.dfs(root)
        return self.ans