文章目录
- 一:形态学基础
- (1)结构元素
- (2)程序
- 二:二值形态学的基础运算
- (1)基本形态变换
- A:膨胀运算
- ①:概述
- ②:示例
- ③:程序
- B:腐蚀运算
- ①:概述
- ②:示例
- ③:程序
- 膨胀和腐蚀性质
- (2)复合形态变换
- A:开、闭运算定义
- B:开、闭运算效果
- C:开、闭运算性质
- D:程序
一:形态学基础
形态学:是图像处理中的一种基本方法,用于对图像中的形状和结构进行分析和处理。形态学基于数学形态学的理论,利用结构元素和形态学运算来改变和提取图像中的形状、边界和纹理等特征
形态学运算:就是用结构元素对图像集合进行操作,观察图像中各部分关系,从而提取有用特征进行分析和描述,以达到对图像进行分析和识别的目的。下面是常见的形态学运算
- 膨胀(Dialation)
- 腐蚀(Eroision)
- 开运算(Opening)
- 闭运算(Closing)
- 击中击不中变换(Hit-or-Miss Transform)
(1)结构元素
结构元素:是形态学运算中的一个重要概念,它是一个小的固定形状模板或窗口,用于在形态学运算中与图像进行卷积操作。结构元素可以是各种形状,例如矩形、圆形、十字形等,其选择取决于所需的操作和应用场景。结构元素的大小和形状对形态学运算的结果具有重要影响。较小的结构元素可以更好地捕捉图像中的细节和小尺度特征,而较大的结构元素则更适用于涉及较大目标的操作。通常,结构元素被定义为二值图像,其中前景像素表示结构元素的形状,背景像素表示结构元素外部
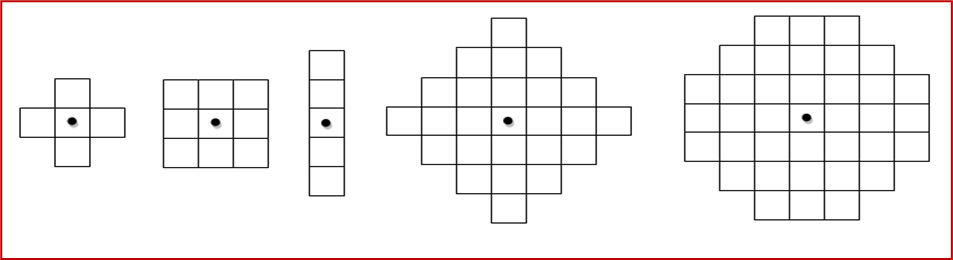
选取结构元素需要遵循以下原则
- 结构元素的几何结构要比原图像简单且有界,且尺寸要明显小于目标图像的尺寸
- 结构元素的形状最好具有某种凸性
- 对于每个结构元素,指定一个原点,作为结构元素参与形态学运算的“参考点”
所有形态学处理都基于填放结构元素的概念。所谓的填放,就是用不同的方法把结构元素放在原图像的内部,在结构元素的填放中引出一系列图像的特性。不同的结构元素和不同的形态学变换可以得到图像不同的处理作用结果
(2)程序
如下:生成一个菱形结构元素

matllab实现:
strel函数是用于创建结构元素的函数,用于形态学图像处理中的运算。结构元素由strel函数根据指定的形状和尺寸创建,并可以用于膨胀、腐蚀、开运算、闭运算等形态学操作。其语法格式如下
se = strel(shape, parameters)
参数
-
shape参数指定了结构元素的形状,可以是以下几种形式之一:'square':正方形结构元素'rectangle':矩形结构元素'disk':圆形结构元素'line':线形结构元素
-
parameters参数是可选的,用于指定结构元素的大小或其他特定参数,具体取决于所选的形状
strel函数返回一个结构元素对象 se,该对象可以用于对图像进行形态学操作。结构元素对象具有一些常用的方法,如膨胀(dilate)、腐蚀(erode)、开运算(open)、闭运算(close)等,可以通过调用这些方法来执行对应的形态学操作
SE = strel('diamond',3);
GN=getnhood(SE)%获取结构元素的邻域
figure,imshow(GN,[]);
Python实现:
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 创建一个菱形结构元素
SE = cv2.getStructuringElement(cv2.MORPH_CROSS, (3, 3))
GN = SE # 获取结构元素的邻域
# 显示邻域图像
plt.imshow(GN, cmap='gray', vmin=0, vmax=1)
plt.axis('off')
plt.show()
二:二值形态学的基础运算
(1)基本形态变换
A:膨胀运算
①:概述
膨胀运算:是形态学运算中的一种基本操作,用于扩展图像中的明亮区域或增加目标的大小。膨胀运算可以通过结构元素与图像进行卷积操作来实现。集合 X X X用结构元素 S S S来膨胀记为 X ⊕ S \boldsymbol{X} \oplus \boldsymbol{S} X⊕S
X ⊕ S = { x ∣ [ ( S ^ ) x ∩ X ] ≠ ∅ } \boldsymbol{X} \oplus \boldsymbol{S}=\left\{\boldsymbol{x} \mid\left[(\widehat{\boldsymbol{S}})_{\boldsymbol{x}} \cap \boldsymbol{X}\right] \neq \varnothing\right\} X⊕S={x∣[(S )x∩X]=∅}
其含义为:对结构元素 S S S作关于原点的映射,所得映射平移为 x x x,形成新的集合为 ( S ^ ) x (\widehat{\boldsymbol{S}})_{\boldsymbol{x}} (S )x,与集合 X X X相交不为空集时结构元素 S S S的参考点的集合即为 X X X被 S S S膨胀所得到的集合
膨胀运算的过程如下
- 将结构元素 S S S的中心放置在图像X的一个像素位置上
- 对于结构元素 S S S中的每个元素,如果该元素对应的图像 X X X的相应位置上有一个非零值(即白色像素),则将该元素的值添加到结果图像的相应位置上
- 重复步骤1和2,直到结构元素 S S S覆盖完整个图像 X X X
- 最终得到的结果图像表示了图像 X X X中所有与结构元素 S S S有交集的像素的并集
膨胀运算的效果是将图像中的边界扩展并填充空洞,增加目标的大小。它可以用于去除小的噪点、连接断开的边界、平滑图像的边缘等应用
膨胀运算代码实现如下
Image=imread('menu.bmp'); %打开图像
BW=im2bw(Image); %转换为二值图像
figure,imshow(BW);
[h w]=size(BW); %获取图像尺寸
result=zeros(h,w); %定义输出图像,初始化为0
for x=2:w-1
for y=2:h-1 %扫描图像每一点,即结构元素移动到每一个位置
for m=-1:1
for n=-1:1 %当前点周围3×3范围,即结构元素为3×3大小
if BW(y+n,x+m) %结构元素所覆盖3×3范围内有像素点为1,即交集不为空
result(y,x)=1; %将参考点记录为前景点
break;
end
end
end
end
end
figure,imshow(result);title('二值图像膨胀');
SE=strel('square',3); %创建结构元素
result1=imdilate(BW,SE); %膨胀运算
figure,imshow(result1);title('二值图像imdilate');
②:示例
示例一:图(a)是一副二值图像,深色“1”部分为目标集合 X X X 。图(b)中深色“1”部分为结构元素 S S S(标有“+”处为原点,即结构元素的参考点)。求 X ⊕ S \boldsymbol{X} \oplus \boldsymbol{S} X⊕S
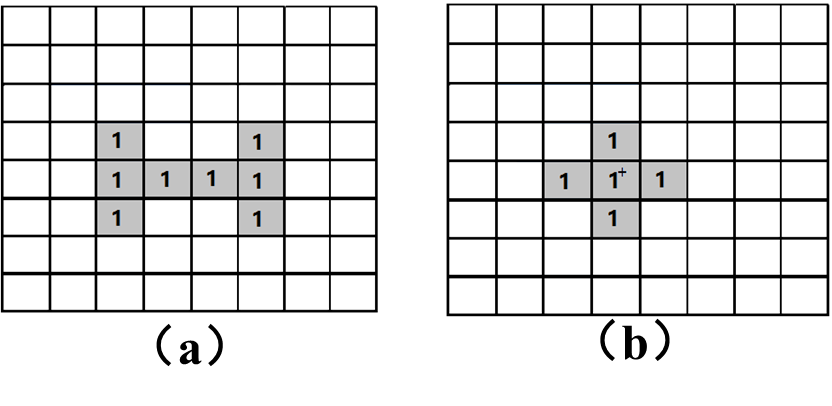
解:图©中深色“1”部分为结构元素 S S S的映射 S ^ \widehat{S} S 。(d)中深色部分;其中,浅灰色“1”部分表示集合 X X X;深灰色“1”部分表示为膨胀(扩大)部分。则整个深色阴影部分就为集合 X ⊕ S \boldsymbol{X} \oplus \boldsymbol{S} X⊕S
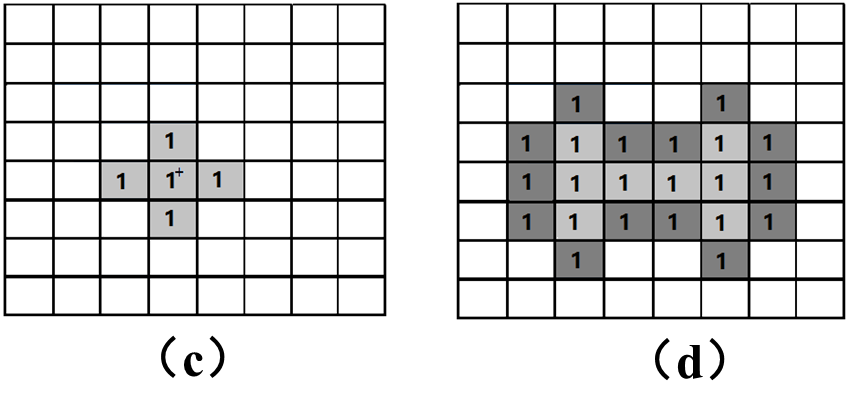
示例二:图(a)中深色“1”部分为目标集合
X
X
X ,图(b)中深色“1”部分为结构元素
S
S
S。 求
X
⊕
S
\boldsymbol{X} \oplus \boldsymbol{S}
X⊕S
解:(c)将
S
S
S映射为
S
^
\widehat{S}
S
,将
S
^
\widehat{S}
S
在
X
X
X上移动,记录交集不为空时结构元素参考点位置,得(d)所示深色阴影部分为膨胀后结果。可看出,目标集合经膨胀后不仅面积扩大,而且相邻两个孤立成分连接
③:程序
如下
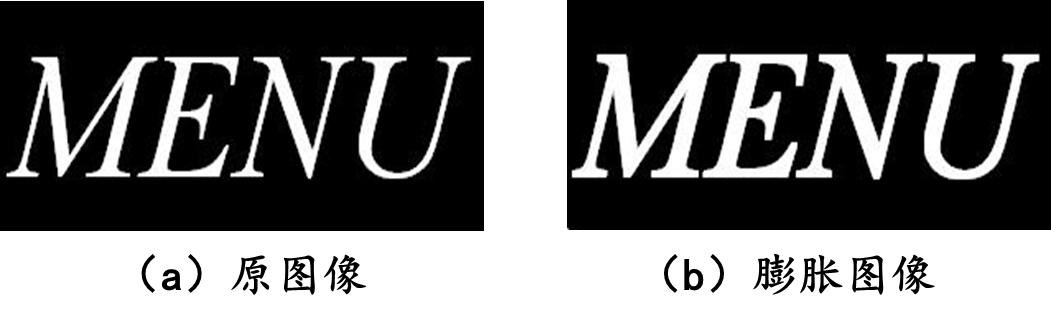
matlab实现:
Image=imread('menu.bmp');
BW=im2bw(Image);
SE=strel('square',3); %创建结构元素
result=imdilate(BW,SE); %膨胀运算
figure,imshow(result);
python实现:
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取图像
Image = cv2.imread('menu.bmp', 0)
# 二值化处理
ret, BW = cv2.threshold(Image, 127, 255, cv2.THRESH_BINARY)
# 创建一个3x3的正方形结构元素
SE = cv2.getStructuringElement(cv2.MORPH_RECT, (3, 3))
# 膨胀运算
result = cv2.dilate(BW, SE)
# 显示结果图像
plt.imshow(result, cmap='gray')
plt.axis('off')
plt.show()
B:腐蚀运算
①:概述
腐蚀运算:是形态学图像处理中的一种基本运算,用于缩小或消除图像中边界或物体的细节。集合 X X X用结构元素 S S S来腐蚀记为 X ⊖ S X \ominus S X⊖S
X
⊖
S
=
{
x
∣
(
S
)
x
⊆
X
}
\boldsymbol{X} \ominus \boldsymbol{S}=\left\{\boldsymbol{x} \mid(\boldsymbol{S})_{\boldsymbol{x}} \subseteq \boldsymbol{X}\right\}
X⊖S={x∣(S)x⊆X}
其含义为:若结构元素
S
S
S平移
x
x
x后完全包括在集合
X
X
X中,记录
S
S
S的参考点位置,所得集合为
S
S
S腐蚀
X
X
X的结果
腐蚀运算代码实现如下
Image=imread('menu.bmp'); %打开图像
BW=im2bw(Image); %转换为二值图像
figure,imshow(BW);
[h w]=size(BW); %获取图像尺寸
result=ones(h,w); %定义输出图像,初始化为1
for x=2:w-1
for y=2:h-1 %扫描图像每一点,即结构元素移动到每一个位置
for m=-1:1
for n=-1:1 %当前点周围3×3范围,即3×3结构元素所覆盖范围
if BW(y+n,x+m)==0 %该范围内有像素点为0,即该位置不能完全包含结构元素
result(y,x)=0; %将参考点记录为背景点,即腐蚀掉
break;
end
end
end
end
end
figure,imshow(result); title('二值图像腐蚀');
SE=strel('square',3); %创建结构元素
result=imerode(BW,SE); %腐蚀运算
figure,imshow(result); title('二值图像imerode');
②:示例
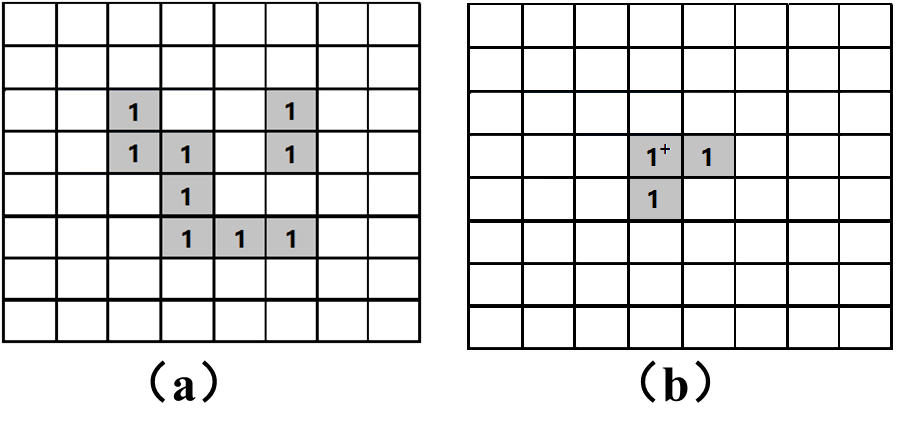
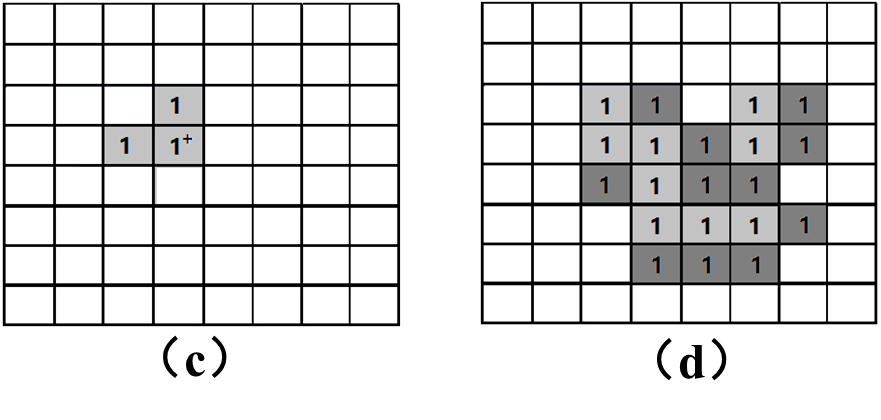
示例:图(a)是一副二值图像,深色“1”部分为目标集合
X
X
X 。图(b)中深色“1”部分为结构元素
S
S
S。求
X
⊖
S
\boldsymbol{X} \ominus \boldsymbol{S}
X⊖S
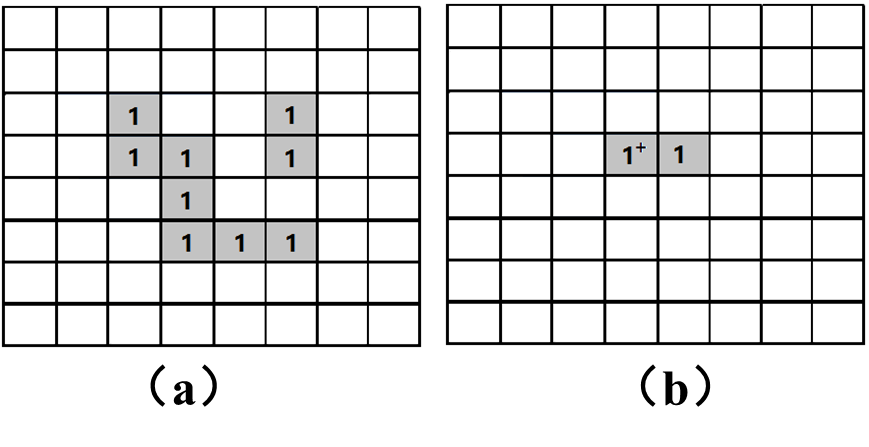
解:当 S S S参考点位于图(c)中红框“1”部分时, ( S ) x ⊆ (S)_x\subseteq (S)x⊆X,则 X ⊖ S X \ominus S X⊖S为图(d)中深灰色“1”部分。白色“0”部分为腐蚀消失部分
③:程序
如下
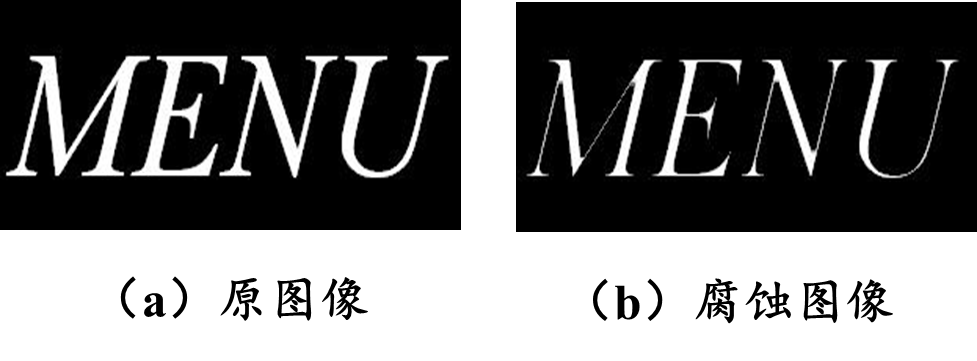
matlab实现:
Image=imread('menu.bmp');
BW=im2bw(Image);
SE=strel('square',3); %创建结构元素
result=imerode(BW,SE); %腐蚀运算
figure,imshow(result);
python实现:
import cv2
import matplotlib.pyplot as plt
# 读取图像
image = cv2.imread('menu.bmp', cv2.IMREAD_GRAYSCALE)
# 二值化
ret, bw = cv2.threshold(image, 127, 255, cv2.THRESH_BINARY)
# 创建结构元素
se = cv2.getStructuringElement(cv2.MORPH_RECT, (3, 3))
# 腐蚀运算
result = cv2.erode(bw, se)
# 显示结果图像
plt.imshow(result, cmap='gray')
plt.show()
膨胀和腐蚀性质
性质1:膨胀和腐蚀运算是关于集合补和映射的对偶关系
( X Θ S ) c = X c ⊕ S ^ ( X ⊕ S ) c = X c S ^ \begin{array}{l}(X \Theta \boldsymbol{S})^{\boldsymbol{c}}=X^{\boldsymbol{c}} \oplus \hat{\boldsymbol{S}} \\(X \oplus \boldsymbol{S})^{\boldsymbol{c}}=X^{\boldsymbol{c}} \boldsymbol{\hat { S }}\end{array} (XΘS)c=Xc⊕S^(X⊕S)c=XcS^
性质2:膨胀运算具有互换性,腐蚀运算不具有
( X ⊕ S 1 ) ⊕ S 2 = ( X ⊕ S 2 ) ⊕ S 1 \left(X \oplus S_{1}\right) \oplus S_{2}=\left(X \oplus S_{2}\right) \oplus S_{1} (X⊕S1)⊕S2=(X⊕S2)⊕S1
性质3:膨胀运算具有结合性
若 S = S 1 ⊕ S 2 , 则有 : X ⊕ S = X ⊕ ( S 1 ⊕ S 2 ) = ( X ⊕ S 1 ) ⊕ S 2 若 S=S_{1} \oplus S_{2} , 则有:X \oplus S=X \oplus\left(S_{1} \oplus S_{2}\right)=\left(X \oplus S_{1}\right) \oplus S_{2} 若S=S1⊕S2,则有:X⊕S=X⊕(S1⊕S2)=(X⊕S1)⊕S2
性质4:膨胀和腐蚀运算具有增长性
X ⊆ Y ⇒ ( X ⊕ S ) ⊆ ( Y ⊕ S ) X ⊆ Y ⇒ ( X ⊖ S ) ⊆ ( Y ⊖ S ) \begin{array}{l}X \subseteq Y \Rightarrow(X \oplus S) \subseteq(Y \oplus S) \\X \subseteq Y \Rightarrow(X \ominus S) \subseteq(Y \ominus S)\end{array} X⊆Y⇒(X⊕S)⊆(Y⊕S)X⊆Y⇒(X⊖S)⊆(Y⊖S)
(2)复合形态变换
一般情况下,膨胀和腐蚀不是互为逆运算的。膨胀和腐蚀进行级连结合使用,产生新的形态变换,即开运算(Opening)和闭运算(Closing)
A:开、闭运算定义
开运算:用结构元素对图像先腐蚀,再膨胀
X ∘ S = ( X ⊖ S ) ⊕ S \boldsymbol{X} \circ \boldsymbol{S}=(\boldsymbol{X} \ominus \boldsymbol{S}) \oplus \boldsymbol{S} X∘S=(X⊖S)⊕S
闭运算:用结构元素对图像先膨胀,再腐蚀
X ⋅ S = ( X ⊕ S ) ⊖ S \boldsymbol{X} \cdot \boldsymbol{S}=(\boldsymbol{X} \oplus \boldsymbol{S}) \ominus \boldsymbol{S} X⋅S=(X⊕S)⊖S
B:开、闭运算效果
开运算效果:
- 删除小物体(滤掉突刺)
- 将物体拆分为小物体(切断细长搭接)起分离作用
- 平滑大物体边界而不明显改变它们面积(平滑图像轮廓)
闭运算效果:
- 填充物体的裂缝和小洞
- 连相近物体(搭接短的间断)起连通补接作用
- 平滑大物体边界而不明显改变它们面积(平滑图像轮廓)
C:开、闭运算性质
性质1:开运算和闭运算都具有增长性
X ⊆ Y ⇒ { ( X ∘ S ) ⊆ Y ( X ⋅ S ) ⊆ Y X \subseteq Y \Rightarrow\left\{\begin{array}{l}(X \circ S) \subseteq Y \\(X \cdot S) \subseteq Y\end{array}\right. X⊆Y⇒{(X∘S)⊆Y(X⋅S)⊆Y
性质2:开运算是非外延的,而闭运算是外延的
X ∘ S ⊆ X X ⊆ X ⋅ S \begin{array}{l}\boldsymbol{X} \circ \boldsymbol{S} \subseteq \boldsymbol{X} \\\boldsymbol{X} \subseteq \boldsymbol{X} \cdot \boldsymbol{S}\end{array} X∘S⊆XX⊆X⋅S
性质3:开运算和闭运算都具有同前性
( X ∘ S ) ∘ S = X ∘ S ( X ⋅ S ) ⋅ S = X ⋅ S \begin{array}{l}(X \circ S) \circ S=X \circ S \\(X \cdot S) \cdot S=X \cdot S\end{array} (X∘S)∘S=X∘S(X⋅S)⋅S=X⋅S
性质4:开运算和闭运算都具有对偶性
( X ∘ S ) c = X c ⋅ S ^ ( X ⋅ S ) c = X c ∘ S ^ \begin{array}{l}(X \circ S)^{c}=X^{c} \cdot \widehat{S} \\(X \cdot S)^{c}=X^{c} \circ \widehat{S}\end{array} (X∘S)c=Xc⋅S (X⋅S)c=Xc∘S
D:程序
如下:

matlab实现:
Image=imread('A.bmp');
BW=im2bw(Image);
SE=strel('square',3);
result1=imopen (BW,SE),SE);
result2=imclose(BW,SE),SE);
figure,imshow(result1) ;title('开运算');
figure,imshow(result2); ;title('闭运算');
python实现:
import cv2
import matplotlib.pyplot as plt
# 读取图像
image = cv2.imread('A.bmp', cv2.IMREAD_GRAYSCALE)
# 二值化
ret, bw = cv2.threshold(image, 127, 255, cv2.THRESH_BINARY)
# 创建结构元素
se = cv2.getStructuringElement(cv2.MORPH_RECT, (3, 3))
# 开运算
result1 = cv2.morphologyEx(bw, cv2.MORPH_OPEN, se)
# 闭运算
result2 = cv2.morphologyEx(bw, cv2.MORPH_CLOSE, se)
# 显示结果图像
plt.subplot(1, 2, 1)
plt.imshow(result1, cmap='gray')
plt.title('开运算')
plt.subplot(1, 2, 2)
plt.imshow(result2, cmap='gray')
plt.title('闭运算')
plt.show()