528. 按权重随机选择（中等）

在这里插入图片描述

思路

我们先把题目读懂。假设我们有数组 w=[1,2,3,4], 那么这个数组的的和为 1+2+3+ 4 = 10 。我们得到 index (0,1,2,3) 的概率为 [1/10,2/10,3/10,4/10]。现在我们要返回(0,1,2,3) 中任意一个 index，但是我们要保证 picklndex()函数所得到这个 index的概率是根据以上的权重来的。
我们可以把每个数拆成一等分：
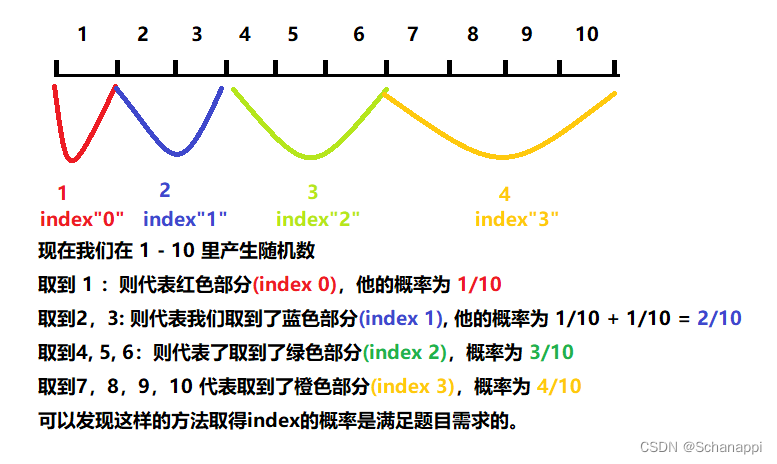
具体算法：先使用 partial_sum 求前缀和（即到每个位置为止之前所有数字的和），这个结果对于正整数数组是单调递增的。每当需要采样的时候，我们可以先随机生成一个数字，然后使用二分法查找其在前缀和中的位置，模拟加权采样的过程。

这里的二分法可以用 lower_bound() 实现。
前缀和 partial_sum

partial_sum()函数定义在头文件中，用于计算某个序列局部元素的和。

函数定义有两种格式
```
OutputIterator partial_sum (InputIterator first, InputIterator last,
                               OutputIterator result);
OutputIterator partial_sum (InputIterator first, InputIterator last,
                               OutputIterator result, BinaryOperation binary_op);
```
其中，first 和 last 都为正向迭代器，[first, last) 用于指定函数的作用范围；result是结果存放的起始位置，result容器要有足够的容量，否则报越界错误；binary_op 用于自定义函数

以 w=[1,2,3,4] 为例，最终会返回 sum = [1,3,6,10] 。
二分查找lower_bound

该函数的使用前提是 数组是非降序列。

它的参数是：
1. 数组元素的地址（或者数组名来表示这个数组的首地址，用来表示这个数组的开头比较的元素的地址，不一定要是首地址，只是用于比较的“首”地址）；
2. 数组元素的地址（对应的这个数组里边任意一个元素的地址，表示这个二分里边的比较的"结尾’地址）；
3. 二分查找的数。
返回值：第一次出现大于等于要查找的数的地址。

代码

class Solution {
public:
    vector<int> sum;
    Solution(vector<int>& w) : sum(std::move(w)){
        // 前缀和 最后还是存放在sum
        partial_sum(sum.begin(), sum.end(), sum.begin());
    }
    
    int pickIndex() {
        // sum.back() 返回sum的最后一个元素，即前缀和的最大值
        // 选择的下标从1开始
        int pos = rand() % sum.back() + 1;
        return lower_bound(sum.begin(), sum.end(), pos) - sum.begin();

    }
};

/**
 * Your Solution object will be instantiated and called as such:
 * Solution* obj = new Solution(w);
 * int param_1 = obj->pickIndex();
 */