机器学习笔记之受限玻尔兹曼机——玻尔兹曼分布介绍
- 引言
- 回顾:Hammersley-Clifford定理
- 玻尔兹曼分布的物理意义
引言
从本节开始,将介绍受限玻尔兹曼机。本节将从马尔可夫随机场开始,介绍玻尔兹曼机分布。
回顾:Hammersley-Clifford定理
在概率图模型——马尔可夫随机场的结构表示中介绍了马尔可夫随机场(Markov Random Field,MRF)以及它的因子分解证明。该证明本质上是基于Hammersley-Clifford定理的表示。Hammersley-Clifford定理主要包含两个部分:
-
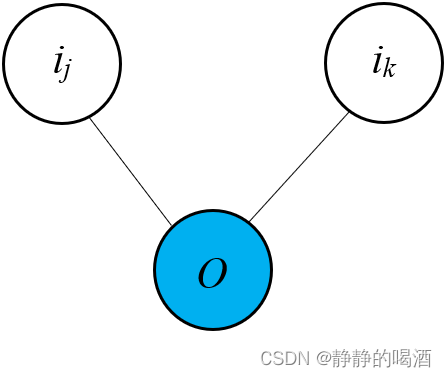
定义1:一个马尔可夫随机场 G \mathcal G G,如果如果两个结点 i j , i k i_j,i_k ij,ik被观测结点 O \mathcal O O阻断,那么 i k , i k i_k,i_k ik,ik基于 O \mathcal O O条件独立:
这里说的‘阻断’是指‘给定观测结点’O \mathcal O O并作为条件。
i j ⊥ i k ∣ O ⇒ P ( i j , i k ∣ O ) = P ( i j ∣ O ) ⋅ P ( i k ∣ O ) i_j \perp i_k \mid \mathcal O \Rightarrow \mathcal P(i_j ,i_k \mid \mathcal O) = \mathcal P(i_j \mid \mathcal O) \cdot \mathcal P(i_k \mid \mathcal O) ij⊥ik∣O⇒P(ij,ik∣O)=P(ij∣O)⋅P(ik∣O)
对应概率图结构表示如下:
这实际上就是‘全局马尔可夫性’(Global Markov Property),局部马尔可夫性、成对马尔可夫性均是由此转化而来。
-
定义2:马尔可夫随机场 G \mathcal G G中关于随机变量集合 X \mathcal X X的联合概率分布 P ( X ) \mathcal P(\mathcal X) P(X)能够将因子分解定义在基于团(Clique)上的恒正函数的乘积,并且这些团覆盖了 G \mathcal G G中所有的结点和边。即:
P ( X ) = 1 Z ∏ i = 1 K ψ i ( x C i ) \mathcal P(\mathcal X) = \frac{1}{\mathcal Z} \prod_{i=1}^\mathcal K \psi_i(x_{\mathcal C_i}) P(X)=Z1i=1∏Kψi(xCi)其中, C i \mathcal C_i Ci表示极大团; x C i x_{\mathcal C_i} xCi表示极大团中结点组成的随机变量集合; ψ i ( x C i ) \psi_i(x_{\mathcal C_i}) ψi(xCi)表示极大团 C i \mathcal C_i Ci对应的势函数(Potential Function),该函数必须是恒正函数; Z \mathcal Z Z表示规范化因子。具体表示如下:
Z = ∑ X ∏ i = 1 K ψ i ( x C i ) = ∑ x 1 , ⋯ , x p ∏ i = 1 K ψ i ( x C i ) \begin{aligned} \mathcal Z & = \sum_{\mathcal X} \prod_{i=1}^{\mathcal K} \psi_i(x_{\mathcal C_i}) \\ & = \sum_{x_1,\cdots,x_p} \prod_{i=1}^{\mathcal K}\psi_i(x_{\mathcal C_i}) \end{aligned} Z=X∑i=1∏Kψi(xCi)=x1,⋯,xp∑i=1∏Kψi(xCi)
可以通过Hammersley-Clifford定理证实定义一和定义二是等价的。 这里在本节中不是重点,感兴趣的小伙伴可移步至这篇博主的文章:Hammersley-Clifford定理证明
一般情况下,为了保证势函数是恒正函数,通常将其假设为指数形式:
指数函数自然是恒正函数。
ψ
i
(
x
C
i
)
=
exp
{
−
E
[
x
C
i
]
}
i
=
1
,
2
,
⋯
,
K
\psi_i(x_{\mathcal C_i}) = \exp \{- \mathbb E[x_{\mathcal C_i}]\} \quad i=1,2,\cdots,\mathcal K
ψi(xCi)=exp{−E[xCi]}i=1,2,⋯,K
并称
−
E
[
x
C
i
]
-\mathbb E[x_{\mathcal C_i}]
−E[xCi]为能量函数(Energy Function)。如果 势函数使用能量函数进行表示,那么联合概率分布
P
(
X
)
\mathcal P(\mathcal X)
P(X)被称为 吉布斯分布(Gibbs Distribution),也称玻尔兹曼分布(Boltzmann Distribution)。
观察,如果势函数使用能量函数表示,那么这个联合概率分布
P
(
X
)
\mathcal P(\mathcal X)
P(X)会产生什么样的变化:
P
(
X
)
=
1
Z
∏
i
=
1
K
ψ
(
x
C
i
)
=
1
Z
∏
i
=
1
K
exp
{
−
E
[
x
C
i
]
}
=
1
Z
exp
[
−
∑
i
=
1
K
E
[
x
C
i
]
]
\begin{aligned} \mathcal P(\mathcal X) & = \frac{1}{\mathcal Z} \prod_{i=1}^{\mathcal K} \psi(x_{\mathcal C_i}) \\ & = \frac{1}{\mathcal Z}\prod_{i=1}^{\mathcal K} \exp \{- \mathbb E[x_{\mathcal C_i}]\} \\ & = \frac{1}{\mathcal Z} \exp \left[- \sum_{i=1}^{\mathcal K} \mathbb E[x_{\mathcal C_i}]\right] \end{aligned}
P(X)=Z1i=1∏Kψ(xCi)=Z1i=1∏Kexp{−E[xCi]}=Z1exp[−i=1∑KE[xCi]]
如果将
−
∑
i
=
1
K
E
[
x
C
i
]
-\sum_{i=1}^{\mathcal K} \mathbb E[x_{\mathcal C_i}]
−∑i=1KE[xCi]看做关于随机变量
x
C
i
x_{\mathcal C_i}
xCi的线性组合,那么上式很明显就是指数族分布(Exponential Families of Distributions)的表达形式:
exp
[
A
(
η
)
]
=
Z
\exp [\mathcal A(\eta)] = \mathcal Z
exp[A(η)]=Z表示归一化因子/配分函数;
A
(
η
)
\mathcal A(\eta)
A(η)表示‘对数配分函数’(log Partition Function).
P
(
x
∣
η
)
=
h
(
x
)
exp
[
η
T
ϕ
(
x
)
−
A
(
η
)
]
=
1
exp
[
A
(
η
)
]
h
(
x
)
exp
[
η
T
ϕ
(
x
)
]
=
1
Z
h
(
x
)
exp
[
η
T
ϕ
(
x
)
]
\begin{aligned} \mathcal P(x \mid \eta) & = h(x) \exp \left[\eta^T \phi(x) - \mathcal A(\eta)\right] \\ & = \frac{1}{\exp [\mathcal A(\eta)]} h(x) \exp \left[\eta^T \phi(x)\right] \\ & = \frac{1}{\mathcal Z}h(x) \exp \left[\eta^T \phi(x)\right] \end{aligned}
P(x∣η)=h(x)exp[ηTϕ(x)−A(η)]=exp[A(η)]1h(x)exp[ηTϕ(x)]=Z1h(x)exp[ηTϕ(x)]
从最大熵原理的角度观察,既然玻尔兹曼斯分布是指数族分布,自然就是概率分布存在约束条件的情况下,满足约束条件基础上熵最大的分布。
这里的约束条件是指:马尔可夫随机场中关于极大团
ψ
i
(
x
C
i
)
\psi_i(x_{\mathcal C_i})
ψi(xCi)的描述。或者说‘马尔可夫随机场’结点之间的条件独立性就是约束条件。
玻尔兹曼分布的物理意义
路德维希·玻尔兹曼是热力学和统计物理学的奠基人之一。在上面出现的一系列名词如:势函数、配分函数、能量函数等,并不是机器学习中的固有概念,而是来源于统计物理学。
假设一个系统状态表示为
S
\mathcal S
S,那么该系统状态的概率分布
P
(
S
)
\mathcal P(\mathcal S)
P(S)表示为:
P
(
S
)
∝
exp
{
−
E
k
B
⋅
T
}
\mathcal P(\mathcal S) \propto \exp \{- \frac{\mathbb E}{k_{\mathcal B} \cdot \mathcal T}\}
P(S)∝exp{−kB⋅TE}
其中
E
\mathbb E
E表示能量函数;
T
\mathcal T
T表示温度;
k
B
k_{\mathcal B}
kB表示玻尔兹曼常数。这里将玻尔兹曼常数 、温度均视作常量,我们关注的重点在于能量函数。
系统状态是可变化的。这里假设一共存在
M
\mathcal M
M种离散状态,各状态对应概率表示如下:
| S \mathcal S S | 1 1 1 | 2 2 2 | ⋯ \cdots ⋯ | M \mathcal M M |
|---|---|---|---|---|
| P ( S ) \mathcal P(\mathcal S) P(S) | P 1 \mathcal P_1 P1 | P 2 \mathcal P_2 P2 | ⋯ \cdots ⋯ | P M \mathcal P_{\mathcal M} PM |
能量函数是一团粒子之间相关的量的表示。粒子的速度会受到其他粒子的干扰,粒子之间发生碰撞时,其速度会发生变化,从而产生能量。将上述公式继续展开:
P
(
S
)
∝
1
exp
{
1
k
B
⋅
T
⋅
E
}
\mathcal P(\mathcal S) \propto \frac{1}{\exp\{\frac{1}{k_{\mathcal B} \cdot \mathcal T} \cdot \mathbb E\}}
P(S)∝exp{kB⋅T1⋅E}1
可以发现,系统状态
S
\mathcal S
S的概率分布和能量函数
E
\mathbb E
E之间呈反比关系。这意味着:能量越大,状态
S
\mathcal S
S的概率越小。
从感性角度理解:能量越大,粒子之间越不稳定,从而越容易挣脱束缚,从而更有机会从当前状态转移至其他离散状态。从而维持当前状态的概率越小。
如果没有外力干扰,最终会向稳定状态收敛。而那时的能量会逐渐降低。
在无向图模型中,同样可以将统计物理学中的概念向机器学习概念中进行映射。例如将一团粒子映射成极大团,粒子可以映射成对应团中的结点。而能量函数也可映射为极大团内各结点之间关联关系的量的表示——势函数。
下一节将介绍受限玻尔兹曼机的模型表示(Representation)。
相关参考:
Hammersley-Clifford定理证明
机器学习-受限玻尔兹曼机(1)-背景介绍-引出玻尔兹曼分布
机器学习-受限玻尔兹曼机(2)-背景介绍-玻尔兹曼分布的形象解释
机器学习-概率图模型6-马尔可夫随机场-Representation-因子分解
玻尔兹曼——百度百科
![[附源码]计算机毕业设计springboot学生宿舍维修管理系统](https://img-blog.csdnimg.cn/5e6c1d0ef6fa47bca850f1e9a7551e24.png)