数字三角形模型：

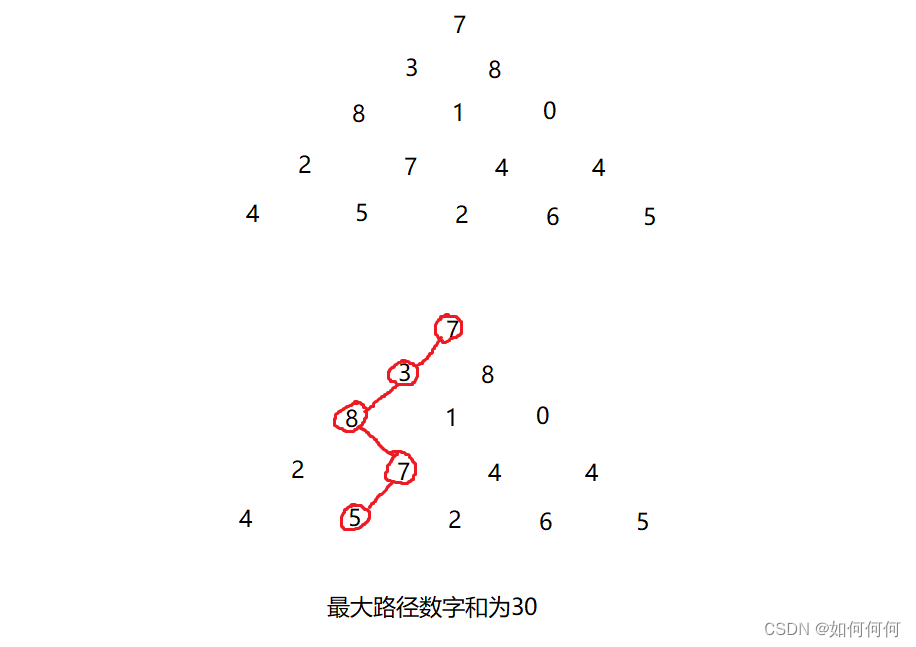
给定一个如下图所示的数字三角形，从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点，一直走到底层，要求找出一条路径，使路径上的数字的和最大。

输入格式：

第一行包含整数 n，表示数字三角形的层数。

接下来 n 行，每行包含若干整数，其中第 i 行表示数字三角形第 i 层包含的整数。

输出格式：

输出一个整数，表示最大的路径数字和。

思路：

对于三角形中的每个点，如果我们走到了该点，那么路径中该点的上一个点一定是左上角的点或者是右上角的点。那么该点的状态一定可以由左上右上两个点的状态推导得到。

从集合的角度考虑：如果将所有走到(i,j)点的路径看做是一个集合，那么该集合可以不重不漏的划分为从左上角走到(i,j)的路径和从右上角走到(i,j)的路径这两个集合。我们要取集合中的最大值，所以取划分出的两个集合中的最大值即可。

f[i][j]表示走到(i,j)点的路径中的最大值，a[i][j]表示(i,j)位置的值。

状态转移方程如下：

f[i][j] = max(f[i - 1][j], f[i - 1][j + 1]) + a[i][j]

因为终点在最后一行，所以我们在三角形的最后一行中寻找最大值即可。

注意这里有边界的问题：我们要保证左上的点和右上的点没有越界才走，并且必须要选择一个点。所以我们可以选着将所有点的初始状态取INF，特别的f[1][1]=g[1][1]。

数字三角形问题一般求的是最大/小值，一般都有边界问题，在更新边界上的值得时候不要被边界外的值影响。

代码如下：

#include<iostream>
#include<cstring>
using namespace std;

const int N = 510;
int g[N][N], f[N][N];//三角形，以每个点为终点的路径的最大值
int n;

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++)//读入地图（其实可以在读入的时候就处理，这里将读入和处理分开了）
        for (int j = 1; j <= i; j++)
            cin >> g[i][j];

    memset(f, -0x3f, sizeof f);//初始化
    f[1][1] = g[1][1];

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= i; j++) {
            if (j - 1 >= 1)f[i][j] = max(f[i][j], f[i - 1][j - 1] + g[i][j]);//如果左上角未越界
            if (j < n)f[i][j] = max(f[i][j], f[i - 1][j] + g[i][j]);//如果右上角未越界
        }

    int res = -0x3f3f3f3f;//在最后一行中找最大值
    for (int i = 1; i <= n; i++)res = max(res, f[n][i]);

    cout << res;
    return 0;
}

例题：

1.摘花生

Hello Kitty想摘点花生送给她喜欢的米老鼠。

她来到一片有网格状道路的矩形花生地（二维矩阵），从西北角进去，东南角出来。

地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生。

Hello Kitty只能向东或向南走，不能向西或向北走。

问Hello Kitty最多能够摘到多少颗花生。

输入格式：

第一行是一个整数T，代表一共有多少组数据。

接下来是T组数据。

每组数据的第一行是两个整数，分别代表花生苗的行数R和列数 C。

每组数据的接下来R行数据，从北向南依次描述每行花生苗的情况。每行数据有C个整数，按从西向东的顺序描述了该行每株花生苗上的花生数目M。

输出格式：

对每组输入数据，输出一行，内容为Hello Kitty能摘到得最多的花生颗数。

思路：

每个点的状态由右边或者是上边的点转移得到。

状态转移方程：

f[i][j] = max(f[i - 1][j], f[i][j - 1]) + g[i][j]

代码如下：

#include<iostream>
using namespace std;

const int N = 1010;
int f[N][N];
int T, n, m;

int main() {
    cin >> T;

    while (T--) {
        cin >> n >> m;

        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++) {
                cin >> f[i][j];
                f[i][j] = max(f[i - 1][j], f[i][j - 1]) + f[i][j];
            }

        cout << f[n][m] << endl;
    }

    return 0;
}