如果有兴趣了解更多相关内容,欢迎来我的个人网站看看:瞳孔空间
一:算法及模型
物理退火过程
什么是退火:是指将固体加热到足够高的温度,使分子呈随机排列状态,然后逐步降温使之冷却,最后分子以低能状态排列,固体达到某种稳定状态。
物理退火过程:
- 加温过程:增强粒子的热运动,消除系统原先可能存在的非均匀态
- 等温过程:对于与环境换热而温度不变的封闭系统,系统状态的自发变化总是朝自由能减少的方向进行,当自由能达到最小时,系统达到平衡态
- 冷却过程:使粒子热运动减弱并渐趋有序,系统能量逐渐下降,从而得到低能的晶体结构
温度越低,物体的能量状态越低,到达足够的低点时,液体开始冷凝与结晶,在结晶状态时,系统的能量状态最低。
- 缓慢降温(退火,annealing)时,可达到最低能量状态
- 快速降温(淬火,quenching)时,会导致不是最低能态的非晶形
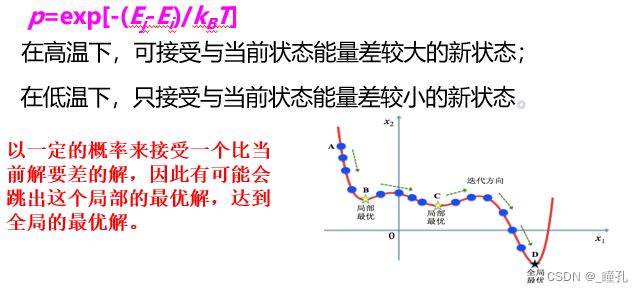
数学表述:在温度T,分子停留在状态r满足Boltzmann概率分布

在同一个温度T,选定两个能量E1<E2,有:
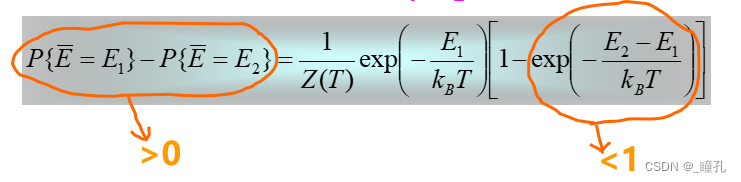
Boltzmann概率分布告诉我们:
- 在同一个温度,分子停留在能量小的状态的概率大于停留在能量大的状态的概率
- 温度越高,不同能量状态对应的概率相差越小;温度足够高时,各状态对应概率基本相同
- 随着温度的下降,能量最低状态对应概率越来越大;温度趋于0时,其状态趋于1
模拟退火算法
模拟退火算法最早的思想由Metropolis等(1953)提出,1983年Kirkpatrick等将其应用于组合优化。是模仿自然界退火现象而得,利用了物理中固体物质的退火过程与一般优化问题的相似性,从某一初始温度开始,伴随温度的不断下降,结合概率突跳特性在解空间中随机寻找全局最优解。
介绍模拟退火前,需要先介绍爬山算法。爬山算法是一种简单的贪心搜索算法,该算法每次从当前解的临近解空间中选择一个最优解作为当前解,直到达到一个局部最优解。
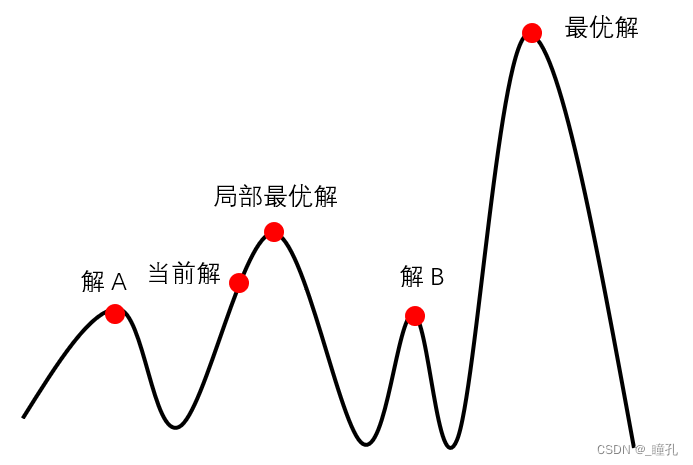
爬山算法实现很简单,其主要缺点是会陷入局部最优解,而不一定能搜索到全局最优解。如上图所示:假设从当前解出发,爬山算法搜索到这个局部最优解就会停止搜索,因为在局部最优解位置无论向那个方向小幅度移动都不能得到更优的解。
而模拟退火算法从某一较高初温出发,伴随温度参数的不断下降,结合一定的概率突跳特性在解空间中随机寻找目标函数的全局最优解,即在局部最优解能概率性地跳出并最终趋于全局最优。如下:
e23b45cc-2379-11eb-905e
关于爬山算法与模拟退火,有一个有趣的比喻:
- 爬山算法:兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法,它不能保证局部最优值就是全局最优值。
- 模拟退火:兔子喝醉了。它随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,它渐渐清醒了并朝最高方向跳去。这就是模拟退火。
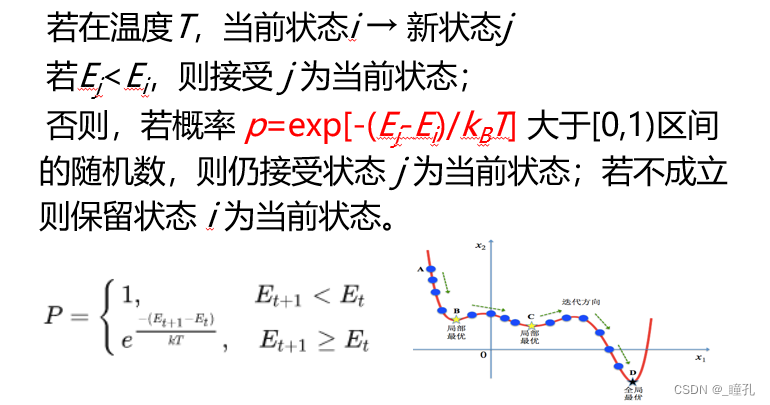
退火算法的基本思想:在一定温度下,搜索从一个状态随机地变化到另一个状态;随着温度的不断下降直到最低温度,搜索过程以概率1停留在最优解。
- 将温度T当作控制参数
- 目标函数值f视为内能E
- 固体在某温度T时的一个状态对应一个解
- 算法试图随着控制参数T的降低,使目标函数f(内能E)也逐渐降低,直至趋于全局最小值(退火中低温时的最低能量状态),就像金属退火过程一样
算法的目的
- 解决NP复杂性问题
- 克服优化过程陷入局部极小
- 克服初值依赖性
Metropolis准则(1953)——以概率接受新状态:固体在恒定温度下达到热平衡的过程可以用Monte Carlo方法(计算机随机模拟方法)加以模拟,虽然该方法简单,但必须大量采样才能得到比较精确的结果,计算量很大。
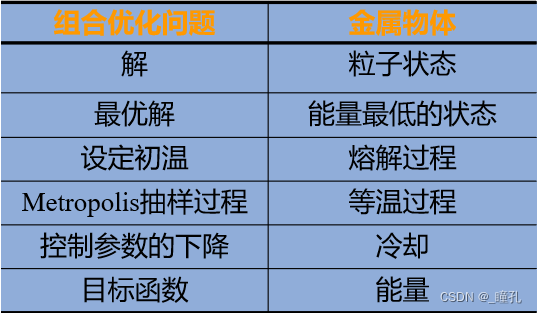
组合优化与物理退火的相似性比较:
模拟退火算法的基本步骤: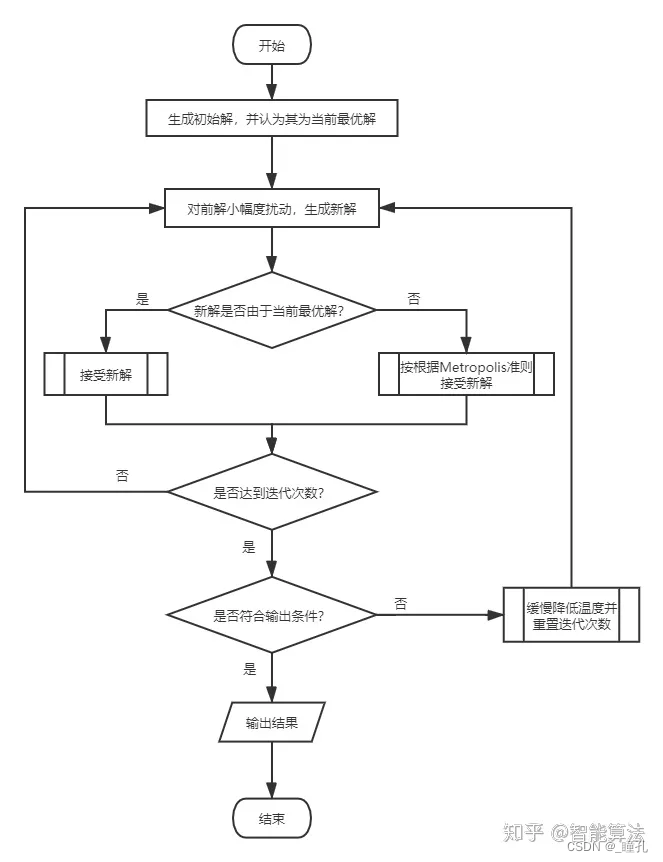
代码表示:

文字表述:

二:应用实例
集成电路设计:利用模拟退火算法进行超大规模集成电路的最优设计,是目前模拟退火算法最成功的应用实例之一。用模拟退火算法几乎可以很好地完成所有优化的VLSI设计工作。如全局布线、布板、布局和逻辑最小化等。
图像处理中的应用:模拟退火算法可用来进行图像恢复等工作,即把一幅被污染的图像重新恢复成清晰的原图,滤掉其中被畸变的部分。因此它在图像处理方面的应用前景是广阔的。
神经网计算机中的应用:模拟退火算法具有跳出局部最优陷阱的能力。在Boltzmann机中,即使系统落入了局部最优的陷阱,经过一段时间后,它还能再跳出来,系统最终将往全局最优值的方向收敛




![[附源码]计算机毕业设计保护濒危动物公益网站Springboot程序](https://img-blog.csdnimg.cn/8e370b9f206f4c05ba155487d4d371e0.png)