目录

⭐一、移除链表元素 

⭐二、反转链表

⭐三、求链表中间节点

⭐四、求链表倒数第k个节点

⭐ 五、合并两个有序链表

⭐六、链表的回文结构

⭐ 七、相交链表

⭐八、环形链表

⭐九、链表入环的第一个节点

---

---

⭐一、移除链表元素 

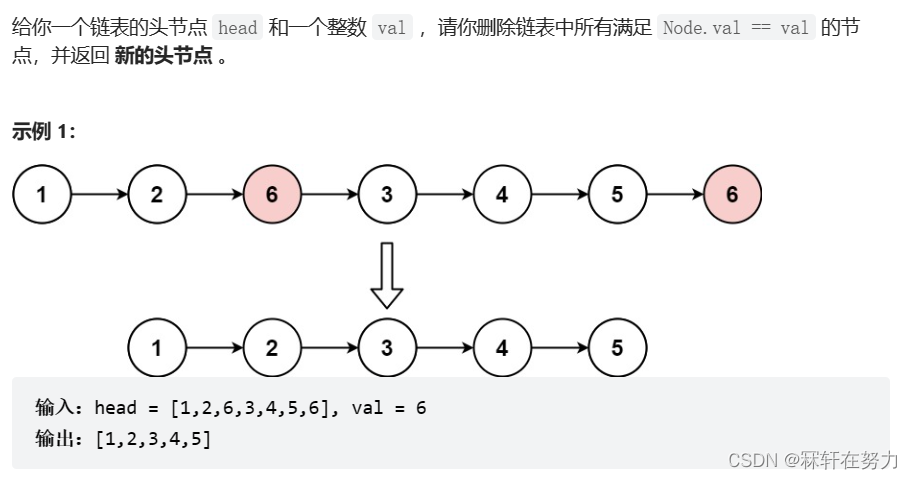
链接： 移除链表元素

思路一：前后指针法

1.定义两个指针cur、prev

cur用来遍历，prev用来指向cur的前一个节点，方便删除时连接链表

2.直接遍历链表，如果该节点的val值与要删除的val值相等，那么就free掉该节点

时间复杂度O（n），空间复杂度O（1）

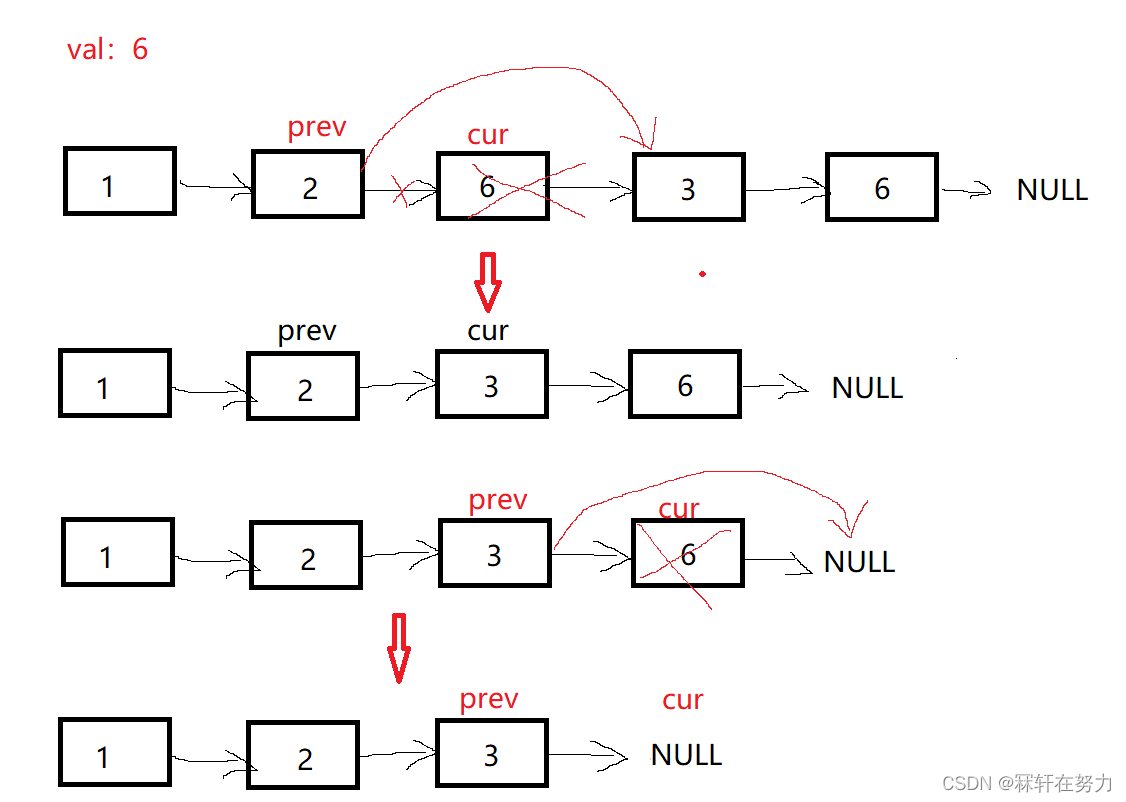
 ⭐代码实现：

struct ListNode* removeElements(struct ListNode* head, int val){
struct ListNode*cur=head,*prev=NULL;
while(cur)
{if(cur->val!=val)
{
 prev=cur;//让prev指向cur节点的前一个节点
 cur=cur->next;
}
else 
{
    if(prev==NULL)//判断删除的是否为头节点
    {
        head=cur->next;//为头节点的话，指向头节点的指针后移
        free(cur);
        cur=head;
    }
    else 
    {
        prev->next=cur->next;//删除节点的前一个节点连上删除节点的后一个节点
        free(cur);
        cur=prev->next;//更新一下cur指向的节点
    }
}


}
return head;
}

注意点:如果删除的节点为头节点时，需要更新一下head头节点。

思路二：

将不等于val的节点尾插到一个新的链表中，等于val的节点直接删除（free掉）

时间复杂度O（n），空间复杂度O（1）

 

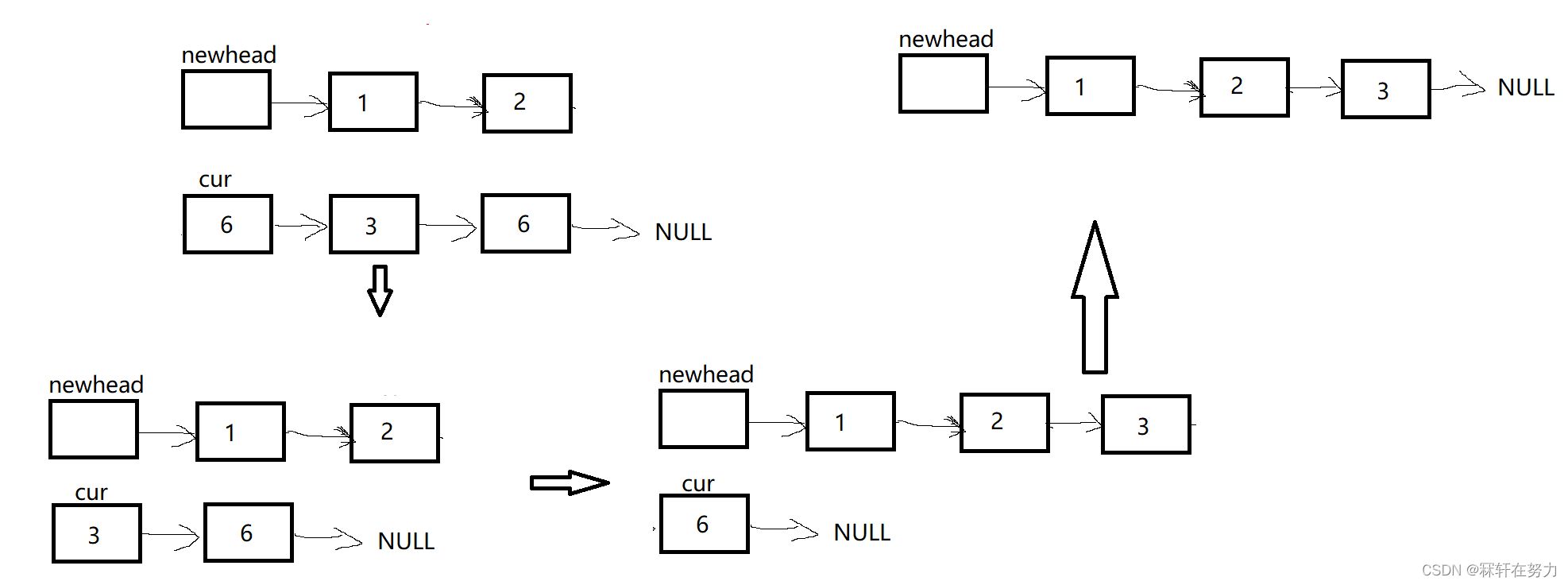
 ⭐代码实现：

struct ListNode*  removeElements(struct ListNode* head, int val) {
    //创建一个什么都不存的头节点（哨兵位节点）
    struct ListNode* newhead = (struct ListNode*) malloc(sizeof(struct ListNode));
    struct ListNode*tail=newhead，*cur = head;
   //tail指向新链表的尾，cur用来遍历新链表
        while(cur!=NULL)
        {
            if(cur->val == val)
            {
                struct ListNode *tmp = cur->next;
                   free(cur);
                   cur=tmp;
            }
            else
            {
                tail->next=cur;
                tail=cur;
                cur=cur->next;
            }
        }

        tail->next=NULL;//注意要把新链表的尾置空
      head=newhead->next;//把新链表赋给head
      free(newhead);
      return head;

    }

1.该方法不需要判断删除的节点是否为头节点，

但需要注意的是

2.得把新链表头节点的下一个节点赋给head，而不是把新链表的头节点赋给head

3.如果最后一个节点是被删除的节点，那么需要把新链表的尾节点置空，不然新链表的尾节点的next将变为野指针

⭐二、反转链表

链接： 反转链表

思路：

将原链表中的节点依次取下来头插到新链表中

图解：

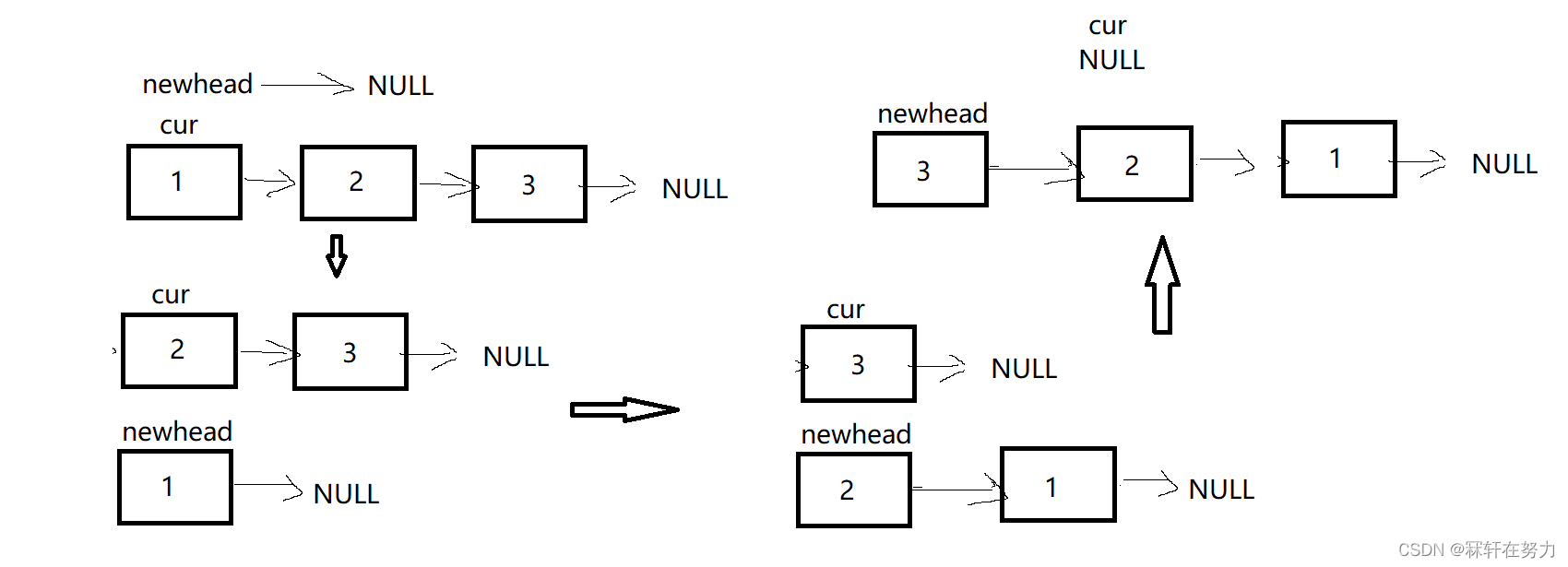
⭐ 代码实现：

struct ListNode* reverseList(struct ListNode* head){

 struct ListNode*newhead=NULL;//新链表的头节点
 struct ListNode*cur=head,*tmp=NULL;
 while(cur)
 {
     tmp=cur;
     cur=cur->next;
     tmp->next=newhead;//头插
     newhead=tmp;
 }   
 return newhead;
}

 时间复杂度O（n），空间复杂度O（1）

⭐三、求链表中间节点

链接：链表的中间节点

 思路：快慢指针法

设置一个快指针fast和一个慢指针slow同时指向头结点，让fast指针一次走两个结点，而slow指针一次走一个结点，如果链表结点个数为奇数，则fast->next为空时，slow就是中间节点，如果链表结点为偶数，则fast为空时，slow就是中间节点，循环结束后，返回slow即可

链表节点为奇数个：

 链表节点为偶数个：

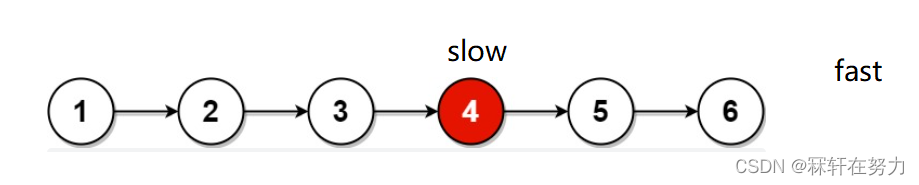
⭐ 代码实现：

struct ListNode* middleNode(struct ListNode* head){

struct ListNode*fast=head,*slow=head;
while(fast&&fast->next)
{
    fast=fast->next->next;//一次走两步
    slow=slow->next;//一次走一步
}

return slow;

}

⭐四、求链表倒数第k个节点

链接：求链表倒数第k个节点

 思路：快慢指针法

先设置两个指针fast 和 slow ，先让fast走k步，并判断如果k值过大，当fast已经为空时，说明k值不合法，返回空。如果K的值合法，那么接着让fast和slow一起走，当fast为空时，slow的位置就是倒数第K个结点

图解：

⭐ 代码实现：

struct ListNode* FindKthToTail(struct ListNode* pListHead, int k ) {
   struct ListNode*fast=pListHead, *slow=pListHead;
     if(!pListHead||k<=0)return NULL;
   while(k--)
   {
    if(fast)
     { 
        fast=fast->next;//fast不为空就走
     }
   else
    {
       return NULL;//fast为空说明不合法，返回NULL
    }
   }
   while(fast)
   {
    fast=fast->next;//fast，slow一起走
    slow=slow->next;
   }
   
   return slow;
}

这里需要注意的是，如果k<=0的时候，说明不合法，K过大时也不合法。

⭐ 五、合并两个有序链表

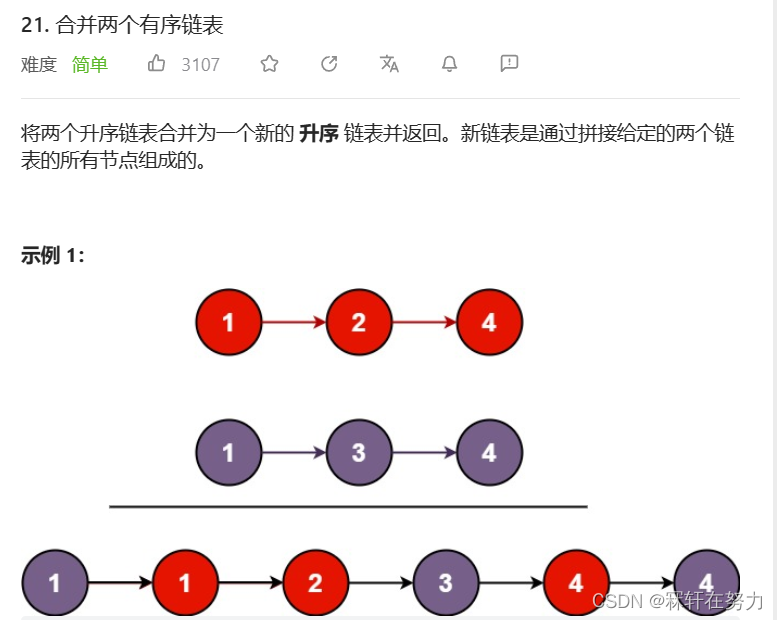
链接：合并两个有序链表

思路：哨兵位解法

创建一个新节点（哨兵位节点，不存放值的节点）作为新链表，比较两个原链表中的val值，取小的尾插至新链表中，省去了判断两个链表是否为空的情况，但返回前需要free掉该空间，时间复杂度O（n）,空间复杂度O（1）

⭐ 代码实现：

struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2){
struct ListNode*phead=NULL,*tail=NULL;
struct ListNode*tmp=NULL;
phead=tail=(struct ListNode*)malloc(sizeof(struct ListNode));
if(list1==NULL)
{
    return list2;
}
if(list2==NULL)
{
    return list1;
}
while(list1&&list2)
{
    if(list1->val<=list2->val)
    {
        tail->next=list1;
        list1=list1->next;
        tail=tail->next;
        tail->next=NULL;
    }
    else{
        tail->next=list2;
        list2=list2->next;
        tail=tail->next;
        tail->next=NULL;
    }
}
if(list1==NULL)
{
      tail->next=list2;
}
else{
    tail->next=list1;
}
  struct ListNode* head=phead->next;
   free(phead);//释放申请的空间，防止内存泄漏
return head;
}

⭐六、链表的回文结构

链接：链表的回文结构

思路：

先找到该链表的中间节点，然后从中间节点开始，将后面的节点依次头插到一个新链表中（反转链表），然后再通过比较这两个链表，如果都相等那么是回文结构，如果有一个节点不相等那么不为回文结构

通过上面的求链表的中间节点和反转链表我们可以很轻松的解决这个问题

⭐代码实现：

class PalindromeList {
public:
    bool chkPalindrome(ListNode* A) {
        // write code here
        ListNode*fast=A;
        ListNode*slow=A;
        ListNode*phead=NULL;
        while(fast&&fast->next)//为了求出中间节点
        {
            fast=fast->next->next;
            slow=slow->next;
        }
        while(slow)//将链表反转
        {
            ListNode*tmp=slow;
            slow=slow->next;
            tmp->next=phead;
            phead=tmp;
        }
        while(phead)
        {
            if(phead->val!=A->val)
            {
                return false;//不相等就返回false
            }
            else {
            phead=phead->next;
            A=A->next;
            }
        }
        return true;
    }
};

⭐ 七、相交链表

链接：相交链表

思路：

先将这两个链表各自遍历一遍，遍历的同时求出它们的长度，并在它们最后一个节点处结束遍历（为了比较它们是否相交，因为相交的话，最后一个节点必相同），然后比较它们最后一个节点是否相等，如果不相等返回空，如果相等，接着比较它们的长度，让长的链表先走它们的长度差步，然后一起走，它们第一个相遇的节点就是它们相交的第一个节点了

⭐代码实现：

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    struct ListNode*pre=headA,*cur=headB;
    struct ListNode*longlist=headA,*shortlist=headB;
    int cnt1=1,cnt2=1;
    while(pre->next)//遍历链表
    {
        cnt1++;//求长度
        pre=pre->next;
    }
    while(cur->next)//遍历链表
    {
        cnt2++;//求长度
        cur=cur->next;
    }
    if(pre!=cur)//比较最后一个节点
    {
         return NULL;//不相等返回空
    }
    if(cnt1<cnt2)
    {
       longlist=headB;//为了让长的先走
       shortlist=headA;
    }
    int a=abs(cnt1-cnt2);//算长度差
    while(a--)
    {
      longlist=longlist->next;//让长的先走它们的长度差步
    }
    while(longlist!=shortlist)//相遇的节点就为第一个相交的节点
    {
       longlist=longlist->next;
       shortlist=shortlist->next;
    }
    return longlist;


}

⭐八、环形链表

链接：环形链表

思路：快慢指针法

让fast和slow指针同时走，不过fast一次走两步，slow指针一次走一步，如果该链表不带环，那么fast和slow将不会相遇，fast走到空时就返回false，如果带环那么它们将相遇。

⭐代码实现：

bool hasCycle(struct ListNode *head) {
    struct ListNode*fast=head,*slow=head;
    while(fast&&fast->next)
    {
      
        slow=slow->next;
        fast=fast->next->next;
        if(fast==slow)
        {
            return true;
        }
    }
    return false;
    
}

为什么快指针每次走两步，慢指针走一步可以它们可以相遇呢？

原因：
假设链表带环，两个指针最后都会进入环，快指针先进环，慢指针后进环。

最好情况：当慢指针刚进环时，可能就和快指针相遇了，

最差情况：两个指针之间的距离刚好就是环的长度。此时，两个指针每移动
一次，之间的距离就缩小一步，不会出现每次刚好是套圈的情况，因此：在慢指针走到一圈之前，
快指针肯定是可以追上慢指针的，此时它们就相遇了。

让我们假设一下，当慢指针进环时，快指针和慢指针之间的距离为N，快指针一次走两步，慢指针一次走一步，每走一步，他们的距离就减1，从N到N-1，到N-2…3，2，1，最后到0，此时两者就相遇了

那么可不可以让快指针一次走多步（三步或三步以上）呢？
快指针一次走3步，走4步，…n步行吗？
这种情况有时是可以的，比如一些特殊情况。

慢指针进环时他们的距离为N，随后到N-2,N-4…，如果N为奇数，那么N-2*n(n为步数)永远不等于0，毕竟指针不能走半步；而如果N为偶数，则N-2 *n就总会有等于0的时候，由此可以知道，快指针一次走3步，可能快慢指针可以相遇，可能不可以。这需要看它们相遇的时机了。

⭐九、链表入环的第一个节点

链接：环形链表||

思路：

先使用上一题的方法：让fast和slow指针同时走，不过fast一次走两步，slow指针一次走一步，如果该链表不带环，那么fast和slow将不会相遇，fast走到空时就返回false，如果带环那么它们将相遇。

然后保存它们相遇的点，接着让慢指针从起始点开始走，快指针从相遇点开始走，它们都是一次走一步，此时它们相遇的点就是链表入环的第一个节点。

⭐代码实现：

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode*fast=head,*slow=head;
    while(fast&&fast->next)
    {
        fast=fast->next->next;
        slow=slow->next;
        if(fast==slow)
        {
            struct ListNode *l1=fast;
            struct ListNode *l2=head;
            while(l1!=l2)
            {
                l1=l1->next;
                l2=l2->next;
            }
            return l1;
        }
    }
    return NULL;
    
}

它们会在环形入口相遇的原因：

H为链表的起始点，E为环入口点，M与判环时候相遇点设:
环的长度为R，H到E的距离为LE到M的距离为X则:M到E的距离为R-X
在判环时，快慢指针相遇时所走的路径长度:
fast: L +X+nR      slow: L+x
注意:
1.当慢指针进入环时，快指针可能已经在环中绕了n圈了，n至少为1
因为:快指针先进环走到M的位置，最后又在M的位置与慢指针相遇
2.慢指针进环之后，快指针肯定会在慢指针走一圈之内追上慢指针
因为:慢指针进环后，快慢指针之间的距离最多就是环的长度，而两个指针在移动时，每次它们的距离都缩减一步，因此在慢指针移动一圈之前快指针肯定是可以追上慢指针的
而快指针速度是慢指针的两倍，因此有如下关系是:2*(L+X)=L+X+nR 
上式可得：L=nR-X (n为1,2,3,4……，n的大小取决于环的大小，环越小n越大)
极端情况下，假设n=1，此时:L=R-X

所以快指针本来要走n圈的，但是此时快指针从相遇点开始走，所以就少走了X步，最终它们的相遇点就在环的入口点了
即:一个指针从链表起始位置走，一个指针从相遇点位置绕环，每次都走一
步，两个指针最终会在入口点的位置相遇

链表的部分相关OJ题就分享到这里了，886！