滤波的基本概念:
滤波是一种信号处理技术。在机器学习中,滤波通常指的是对输入信号进行加工,以消除噪声、平滑信号或突出特定频率范围的信号
简言之:加工输入,达到理想信号。
用生活的例子来解释:
假设你正在听一首音乐,但是在你的音响系统中有一些杂音。这些杂音可能是由于电源干扰、线缆干扰或其他环境因素引起的。你希望消除这些杂音,以便更好地聆听音乐。
在这种情况下,你可以将滤波器比作一个信号处理器,用于消除杂音。滤波器接收音乐信号作为输入,并根据其设计目标对信号进行处理。例如,低通滤波器可以通过消除高频噪声来使音乐更加平滑,而高通滤波器可以突出音乐中的高频成分,减少低频杂音的影响。这样,滤波器可以改变信号的特性,使你能够更好地享受音乐,而不被杂音干扰。
简言之:加工音乐,达到理想音乐
补充说明:信号和噪声的区别
信号是包含有用信息的电气或物理量,噪声是指在信号获取、传输或处理过程中引入的干扰。(在通信中,“电气”指的是与电信号相关的物理量,包括电压、电流、电磁波等)
线性滤波与非线性滤波的区别:
线性滤波器:
1.线性滤波器的输出是输入信号与滤波器冲击响应之间的线性组合。
假设我们有一个线性滤波器,其冲击响应为 h(t)。如果我们将输入信号 x(t) 与该冲击响应进行卷积,得到输出信号 y(t),即:
y(t) = x(t) * h(t)
(其中,* 表示卷积运算。这个公式描述了线性滤波器的输出是输入信号与滤波器冲击响应之间的线性组合。)
简单来说线性滤波器就是 输入信号跟滤波器做卷积。
2.输入信号与滤波器的冲击响应进行卷积操作。线性滤波具有可加性和比例性的特点
可加性:即
f(x+y) = f(x) + f(y)
假设我们有一台收音机,可以接收两个不同的广播电台发出的信号。我们将这两个信号输入到同一个滤波器中进行处理,那么输出信号就等于每个信号单独经过滤波器处理后的输出信号的总和。这意味着,如果我们想要听到两个电台发出的信号,我们可以将它们分别输入到同一个滤波器中进行处理,然后将滤波器的输出信号相加即可得到最终的信号。
比例性:即
f(cx) = cf(x)
假设我们有一台音响系统,音量控制旋钮可以调节输出信号的幅度。如果我们将输入信号输入到滤波器中进行处理,那么输出信号的幅度也会受到音量控制旋钮的影响。这意味着,如果我们将旋钮向右旋转,增加音量,那么输出信号的幅度也会相应地增加;如果我们将旋钮向左旋转,减小音量,那么输出信号的幅度也会相应地减小。
时域滤波与频域滤波的区别:
时域滤波直接在时间域中对信号进行滤波处理,而频域滤波是将信号从时域转换到频域进行滤波处理,然后再将信号转换回时域。
时域滤波直接操作信号的时间序列,而频域滤波利用信号的频谱信息进行处理。
简言之:时域滤波借助时间,频域滤波借助频率。在处理上,时域滤波直接对时间序列上的信号处理,以时间序列的信号输出。频率滤波插入了“转换信号”的一步即时频转换,最终还是以时间序列的信号输出。
时域滤波与频域滤波的共同点:
最终输出的信号都是一个时域信号
生活的例子说明各自的操作特点:
时域滤波
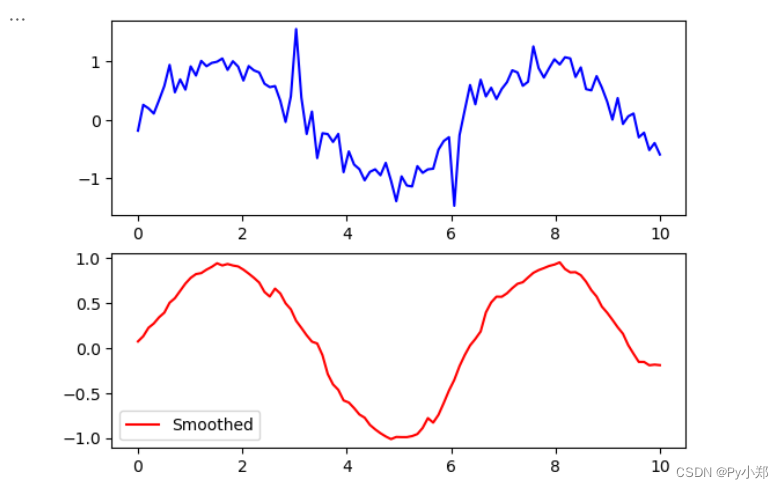
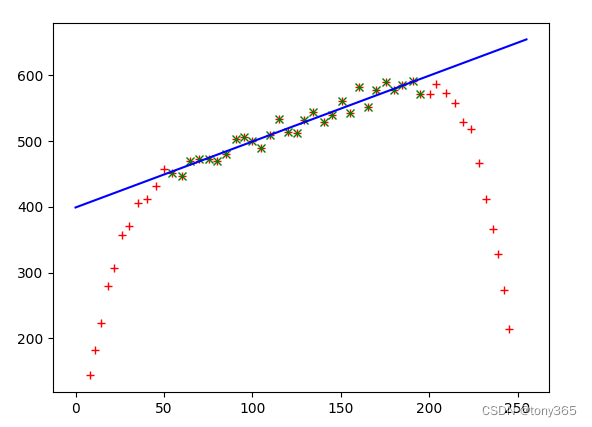
假设你正在录制一段音频,录音时有一些杂音干扰进入了录音中。如果你想去除这些杂音,你可以使用一个时域滤波器,例如移动平均滤波器。该滤波器通过在每个时间点上计算当前时刻和前几个时刻的平均值,对音频信号进行平滑处理,从而减少杂音的影响。这种滤波过程直接在时间域中对信号进行操作,从而改变信号的特性。
如图所示:
频域滤波
在频域中,信号可以表示为一系列频率和幅度的组合,因此可以选择性地增强或抑制特定频率范围的成分 。
假设你希望去除低频背景噪声,保留高频声音的细节,你可以使用频域滤波器,如高通滤波器。首先,你可以将音频信号转换到频域,得到频谱表示。然后,你可以选择性地过滤掉低频成分,然后将信号转换回时域,得到滤波后的输出信号。这种频域滤波过程利用信号的频谱信息,可以有选择地增强或抑制特定频率范围的成分,从而实现对信号的滤波处理。
学习最基本的时域滤波方法
均值滤波
原理:
将每个像素周围的邻域取平均值,然后用这个平均值来代替该像素的原始值。
它会使图像的像素变得模糊。不仅减少噪声,也会减少细节。
算法步骤:
定义一个固定大小的窗口(通常是一个矩形或正方形区域),窗口大小通常是奇数,例如3x3、5x5等。窗口的大小决定了滤波的范围。
遍历图像的每个像素,将当前像素作为窗口中心。
在窗口内获取所有像素的值。
计算窗口内像素值的平均值。
使用平均值来替换窗口中心的像素值。
继续遍历下一个像素,重复步骤2-5,直到处理完整个图像。
通俗的解释:比方说我现在关注位置在[i,j]的像素点即image[i][j],假设我使用3*3的窗口
我要获得这个点经过均值滤波的值,只需要以这个点为中心,画一个3*3的窗口,把这个窗口所覆盖的点的像素值求和再除以9 ,则可以得到均值滤波后的值。
也就是宽从[j-1,i+1],高从[i-1,i+1],这么一个3*3的窗口,对它求平均。
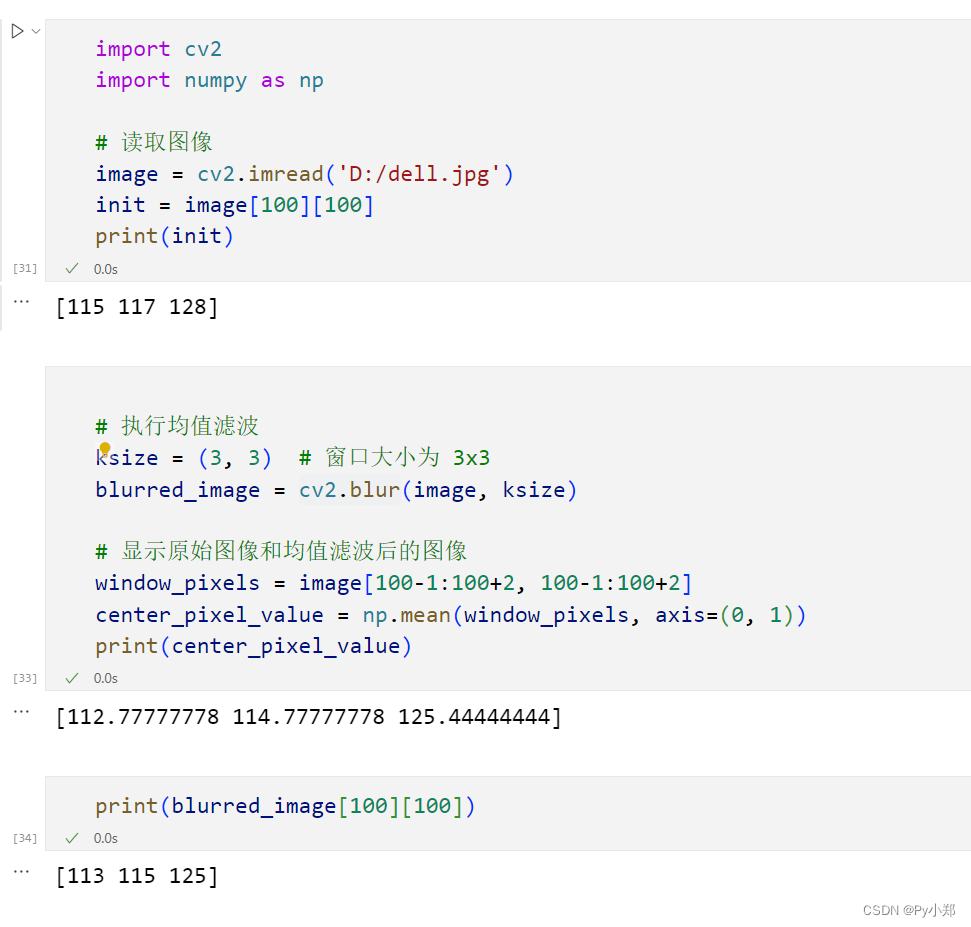
让我们来验证一下:
blurred_image是调用cv2得到的均值滤波后的图像。会发现它的[100][100]处的像素值和我们手动计算的像素值十分接近,说明计算方法确实如此。
接着遍历所有点就可以。但是会碰到一种情况,边界的点,周围没有点如何解决:
在 OpenCV 的
cv2.blur()函数中,边缘像素的处理是通过对图像应用边界扩展。(Border Extension)策略来解决的。具体来说,cv2.blur()函数会自动对图像进行边界扩展,以确保在窗口滑动到边缘像素时,仍然可以获取到足够的像素值进行滤波计算。
代码实现:
import cv2
# 读取图像
img = cv2.imread('image.jpg')
# 进行均值滤波
kernel_size = (5, 5) # 定义卷积核大小
img_blur = cv2.blur(img, kernel_size)
# 显示原图和滤波后的图像
cv2.imshow('Original Image', img)
cv2.imshow('Blurred Image', img_blur)
cv2.waitKey(0)
cv2.destroyAllWindows()
了解相关的频率滤波
-
低通滤波 (Low-Pass Filtering):低通滤波器允许通过低频信号,并削弱或阻止高频信号。它的原理是在频域上去除高频分量,只保留低频分量。低通滤波常用于去除高频噪声或平滑信号。例如,可以使用低通滤波器来平滑图像并去除图像中的细节或噪声。
-
高通滤波 (High-Pass Filtering):高通滤波器允许通过高频信号,并削弱或阻止低频信号。它的原理是在频域上去除低频分量,只保留高频分量。高通滤波常用于强调图像或信号中的边缘、纹理或其他高频特征。例如,可以使用高通滤波器增强图像的边缘。
-
带通滤波 (Band-Pass Filtering):带通滤波器允许通过特定的频率范围内的信号,并削弱或阻止其他频率范围内的信号。它的原理是在频域上选择一个频率范围,去除其他频率范围的分量。带通滤波常用于信号处理中需要提取特定频率范围内的信号或去除其他频率范围的干扰。
这些滤波方法在频域中操作,可以对信号进行选择性地增强或减弱特定频率分量。滤波效果取决于滤波器的特性和参数设置,以及信号的频谱特征。合适的滤波方法选择和参数调整可以有效地提取或去除信号中的特定信息,帮助实现信号处理的目标