Flowable-Modeler功能

• 提供可视化编辑器，编辑BPMN流程，编辑CASE模型，编辑Form表单，编辑App应用，编辑决策表
• 提供可视化参数配置：每个流程可以配置详细的参数设置，按照流程对应的规范来设计。
• 提供导入导出功能：方便将流程结果导入到其他应用程序

Flowable-Modeler界面之流程介绍

界面如下：

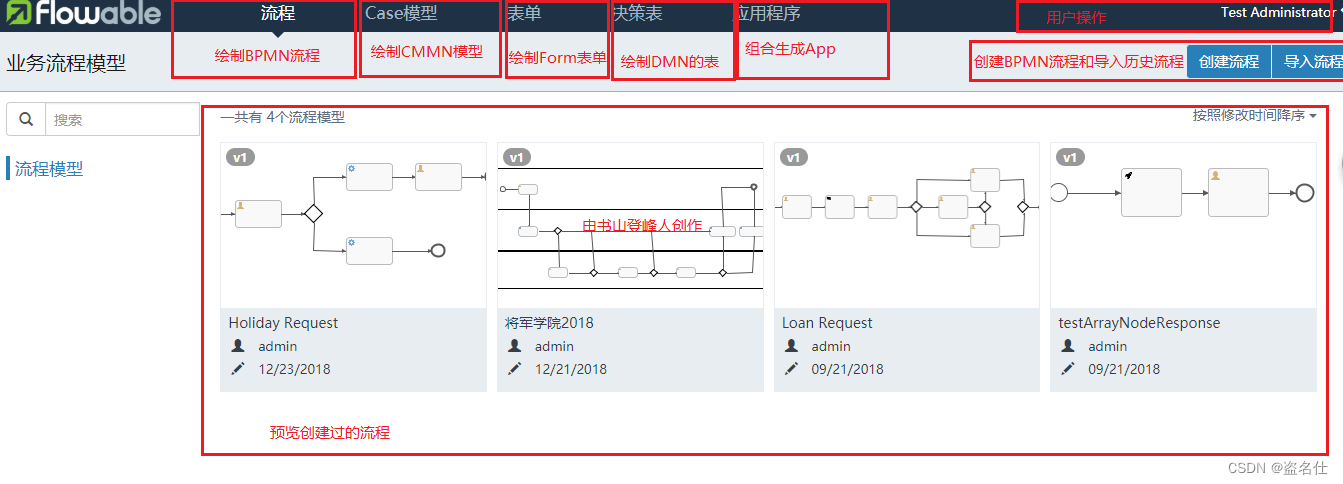
• 该页面的核心功能如图上方框内所述
• 该页面为BPMN的流程管理页面，默认的页面是流程处理页面
• 点击某个流程，可以编辑历史创建过的流程
• 点击创建流程，可以创建一个新的流程

Flowable-Modeler之创建流程

1.点击创建流程：

2.单击创建新模型，进入模型创建页面

 

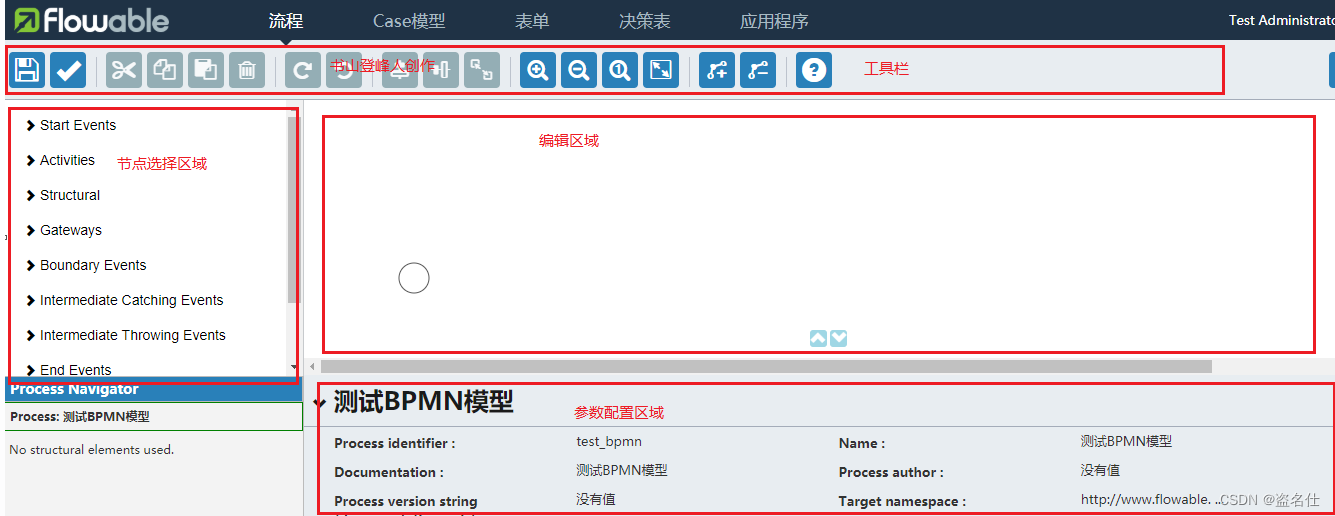
3.工具栏功能：

 

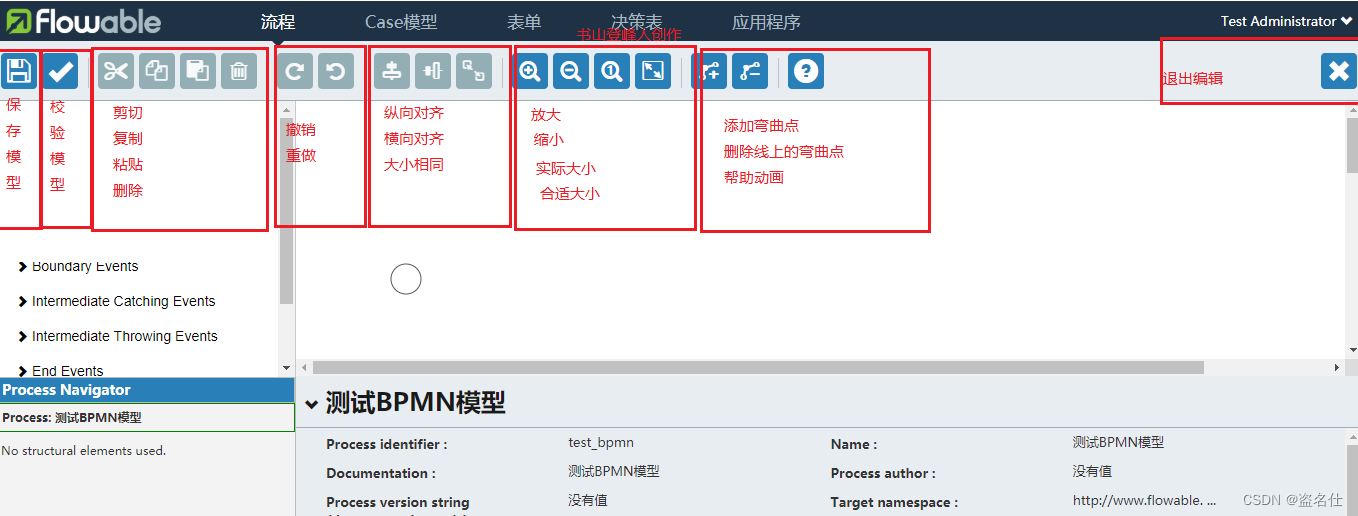
4.节点选择页面我们在后面的章节详细描述

5.单击保存可以配置完成流程保存，进入流程预览页面。

 

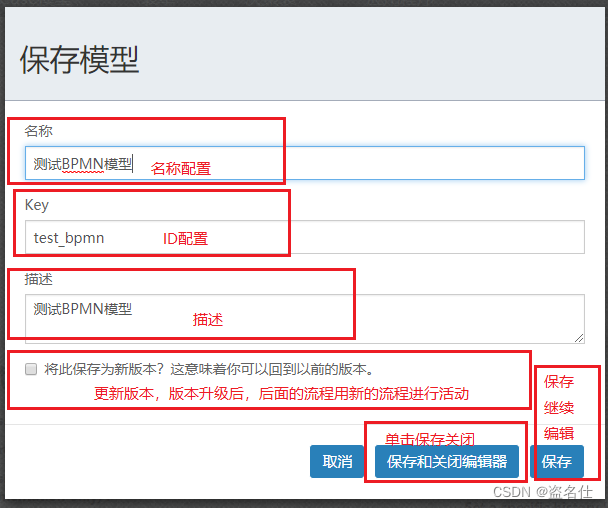
6.进入预览页面

 

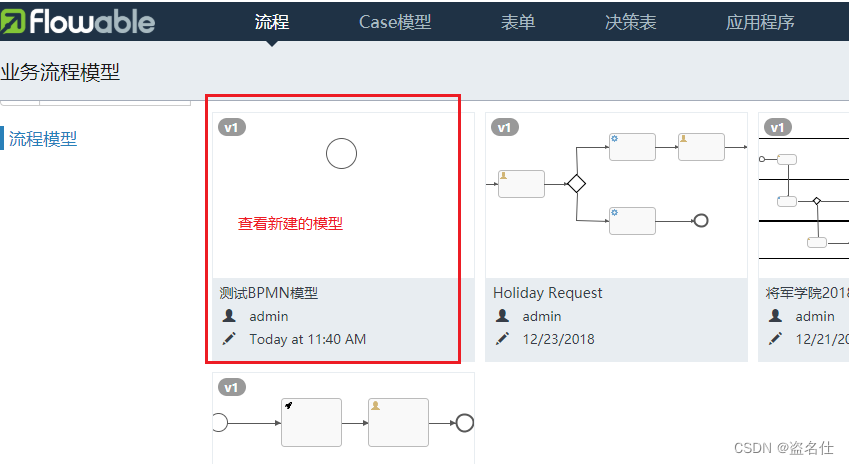
7.单击我们编辑的流程，进入该流程的预览页面，如下图所示：

 

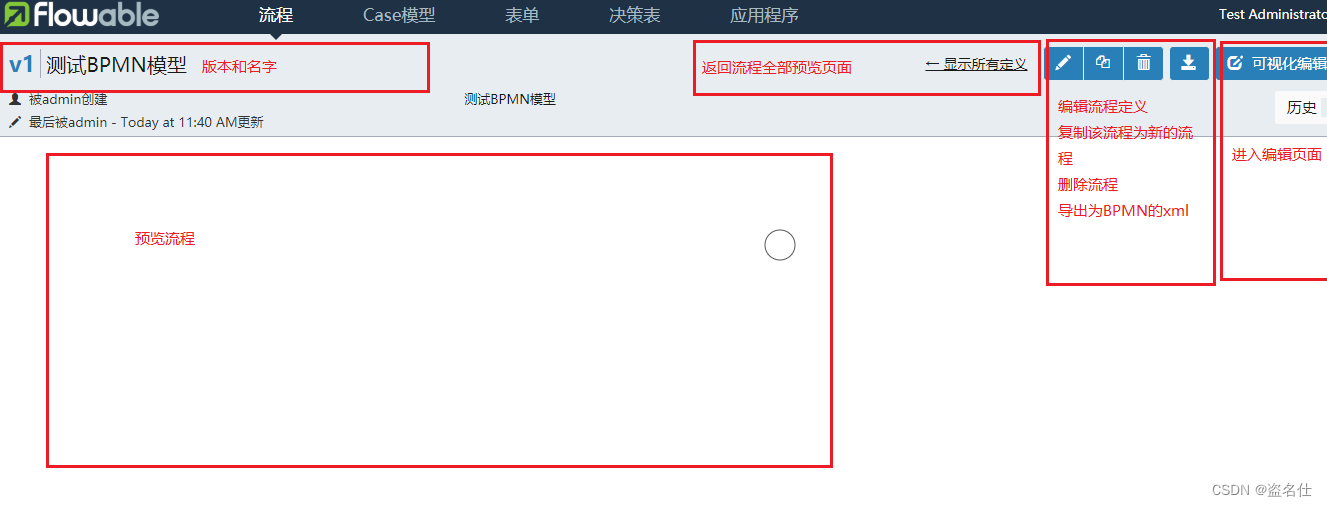
8.单击导出查看生成的xml如下：

<?xml version="1.0" encoding="UTF-8"?>
<definitions xmlns="http://www.omg.org/spec/BPMN/20100524/MODEL" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" xmlns:xsd="http://www.w3.org/2001/XMLSchema" xmlns:flowable="http://flowable.org/bpmn" xmlns:bpmndi="http://www.omg.org/spec/BPMN/20100524/DI" xmlns:omgdc="http://www.omg.org/spec/DD/20100524/DC" xmlns:omgdi="http://www.omg.org/spec/DD/20100524/DI" typeLanguage="http://www.w3.org/2001/XMLSchema" expressionLanguage="http://www.w3.org/1999/XPath" targetNamespace="http://www.flowable.org/processdef">
  <process id="test_bpmn" name="测试BPMN模型" isExecutable="true">
    <documentation>测试BPMN模型</documentation>
    <startEvent id="sid-8DD436F7-D521-433A-A220-F81B1AAD3C84"></startEvent>
  </process>
  <bpmndi:BPMNDiagram id="BPMNDiagram_test_bpmn">
    <bpmndi:BPMNPlane bpmnElement="test_bpmn" id="BPMNPlane_test_bpmn">
      <bpmndi:BPMNShape bpmnElement="sid-8DD436F7-D521-433A-A220-F81B1AAD3C84" id="BPMNShape_sid-8DD436F7-D521-433A-A220-F81B1AAD3C84">
        <omgdc:Bounds height="30.0" width="30.0" x="227.0" y="38.0"></omgdc:Bounds>
      </bpmndi:BPMNShape>
    </bpmndi:BPMNPlane>
  </bpmndi:BPMNDiagram>
</definitions>