1.关于二分搜索常见的误区

区间的定义：

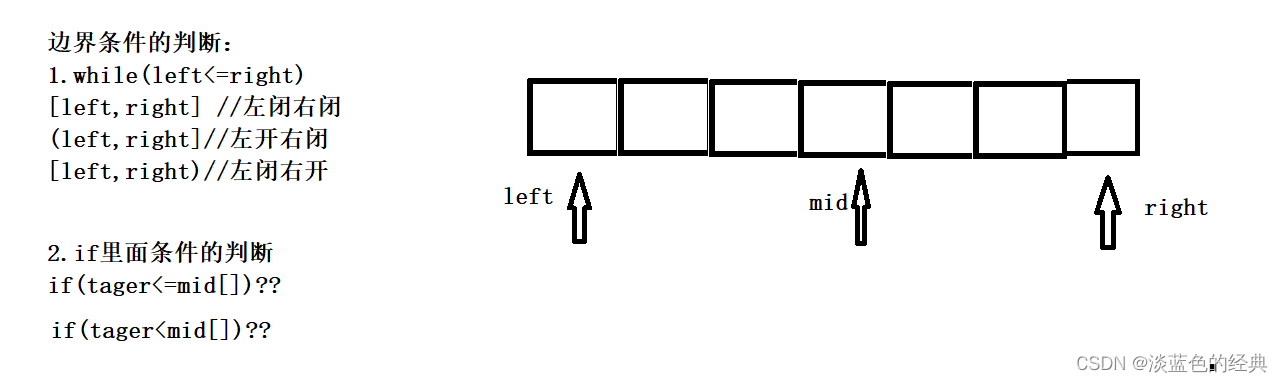
2.左闭右闭区间的写法

class Solution {
public:
    int search(vector<int>& nums, int target)
    {
        int left = 0;
        int right = nums.size() - 1; //因为包含了右区间，所以需要减一
        while (left <= right)  //左闭右闭[1,1],合法，所以left可以等于right
        {
            int mid = (left + right) / 2;
            if (target < nums[mid])
            {
                right = mid - 1; //中间值已经不是target了
            }
            else if (target >nums[mid])
            {
                left = mid + 1;  
            }
            else return mid;
        }
        return -1;
    }
private:
    
};

3.左闭右开区间的写法

class Solution {
public:
    int search(vector<int>& nums, int target)
    {
        int left = 0;
        int right = nums.size(); //因为不包含了右区间，右区间是开放的，所以不需要-1
        while (left < right)  //左闭右闭[1,1),不合法，所以left不等于right
        {
            int mid = (left + right) / 2;
            if (target < nums[mid])
            {
                right = mid ; //因为右区间不包含mid,所以right可以等于mid
            }
            else if (target > nums[mid])
            {
                left = mid + 1;
            }
            else return mid;
        }
        return -1;
    }
private:

};

4.找到第一个大于target的数

class Solution {
public:
    int search(vector<int>& nums, int target)
    {
        int left = 0;
        int right = nums.size() - 1; //因为包含了右区间，所以需要减一
        while (left <= right)  //左闭右闭[1,1],合法，所以left可以等于right
        {
            int mid = (left + right) / 2;
            if (target >=nums[mid])
            {
                left = mid + 1;   
            }
            else
            {
                right = mid - 1; //中间值已经不是target了
            }
        }
        return left;
    }
private:  
};

5.找到第一个小于target的数

int search(vector<int>& nums, int target)
    {
        int left = 0;
        int right = nums.size() - 1; //因为包含了右区间，所以需要减一
        while (left <= right)  //左闭右闭[1,1],合法，所以left可以等于right
        {
            int mid = (left + right) / 2;
            if (target <=nums[mid])
            {
                right = mid - 1; //中间值已经不是target了
            }
            else
            {
                left = mid + 1;   
            }
        }
        return right;
    }

6.找到第一个大于等于taregt的数

 class Solution {
public:
    int search(vector<int>& nums, int target)
    {
        int left = 0;
        int right = nums.size() - 1; //因为包含了右区间，所以需要减一
        while (left <= right)  //左闭右闭[1,1],合法，所以left可以等于right
        {
            int mid = (left + right) / 2; 
            if (target >nums[mid])
            {
                left = mid + 1;   
            }
             else 
            {
                right = mid - 1; //中间值已经不是target了
            }
        }
        return left;
    }
private:  
};

7.找到第一个小于等于target的数

int search(vector<int>& nums, int target)
    {
        int left = 0;
        int right = nums.size() - 1; //因为包含了右区间，所以需要减一
        while (left <= right)  //左闭右闭[1,1],合法，所以left可以等于right
        {
            int mid = (left + right) / 2;
            if (target <nums[mid])
            {
                right = mid - 1; //中间值已经不是target了
            }
            else
            {
                left = mid + 1;   
            }
        }
        return right;
    }