老早以前在学习初等函数的时候，线性函数中的两直线y = m0x + b0, y = m1x +b1如果垂直，则有结论两条直线的斜率乘积为-1即m0*m1 = -1，以前也只是拿来用，没有证明过。最近在学图形学的时候，突然想起了这个点，因此记一篇笔记，证明一下。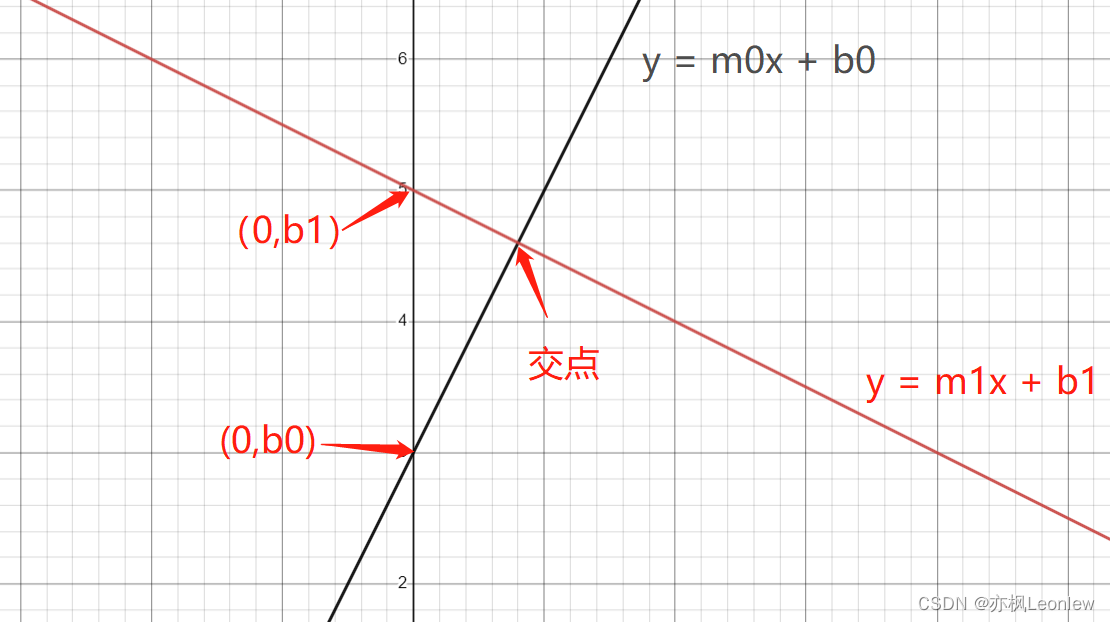

         如上图所示，有两条直线： 和 ，它们相互垂直。这里可以得到一个隐含的条件是：   (斜率相等，y轴截距不同的两条直线是平行的，垂直的话则斜率不等)。

        图中两条直线的交点的坐标，我们可以通过求解方程得到，交点的y是相同的，因此我们有：

        

        求解得到交点的x坐标为：,

         将x分别代入y0和y1,得到交点的y坐标分别为：

          和 ，这两个值是相等的

        因此，图中三个关键的点坐标如下：

        直线y0在y轴的交点A坐标为(0,b0)

        直线y1在y轴的交点B坐标为(0,b1)

        两直线交点C坐标为 这两个坐标对应同一个点。

        由于两条直线垂直，由勾股定理可知，斜边AB距离的平方 = 直角边AC距离的平方 + 直角边BC距离的平方。

        根据两点之间的距离公式，可以得到下面的等式：

        AB的距离的平方 = 

        AC的距离的平方 =   (用C的第一种形式做距离计算，可以减掉b0)

        BC的距离的平方 = （用C的第二种形式做距离计算，可以减掉b1）

        根据勾股定义，可得：

        

        整理一下，得到：

        

        约掉(b1- b0)^2，整理得到：

        

        展开平方差：

        

        整理得到

        , 因此