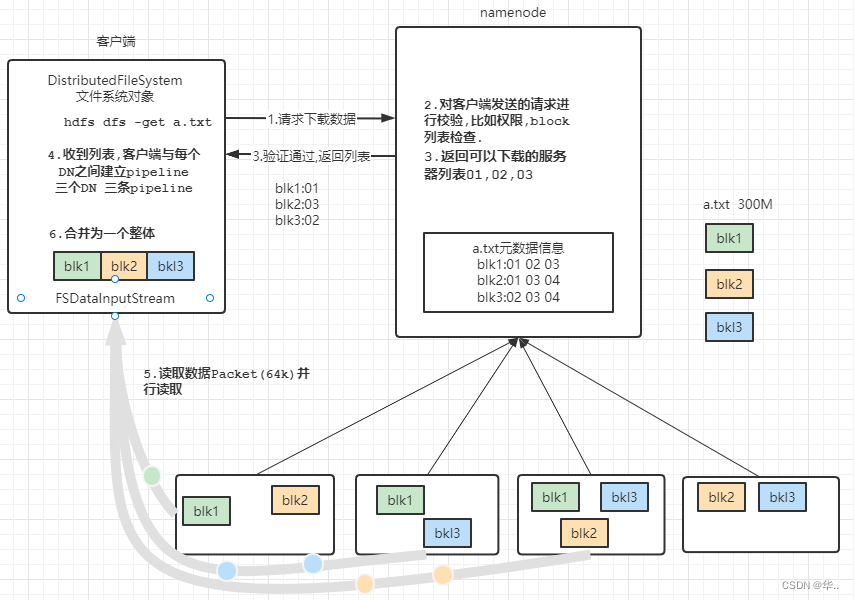
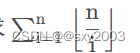Java高阶数据结构图补充-拓扑排序

news2024/11/24 12:44:49

拓扑排序

@

文章目录

Java高阶数据结构 & 图补充-拓扑排序
1. 什么是拓扑排序
2. 拓扑排序算法思想-卡恩算法
3. 拓扑排序代码实现
3.1 遍历链表计算入度
3.2 挑选一个入度为0的顶点
3.3 输出顶点
3.4 判断循环结束是否为全-1
3.4 *kahn*方法
3.5 测试

Java高阶数据结构 & 图补充-拓扑排序

1. 什么是拓扑排序

图片来源：简单、快速地带你了解图论以及拓扑排序！_哔哩哔哩_bilibili

讲得很好哦！

这里我以羊了个羊小游戏这款砖块消除类小游戏为例：

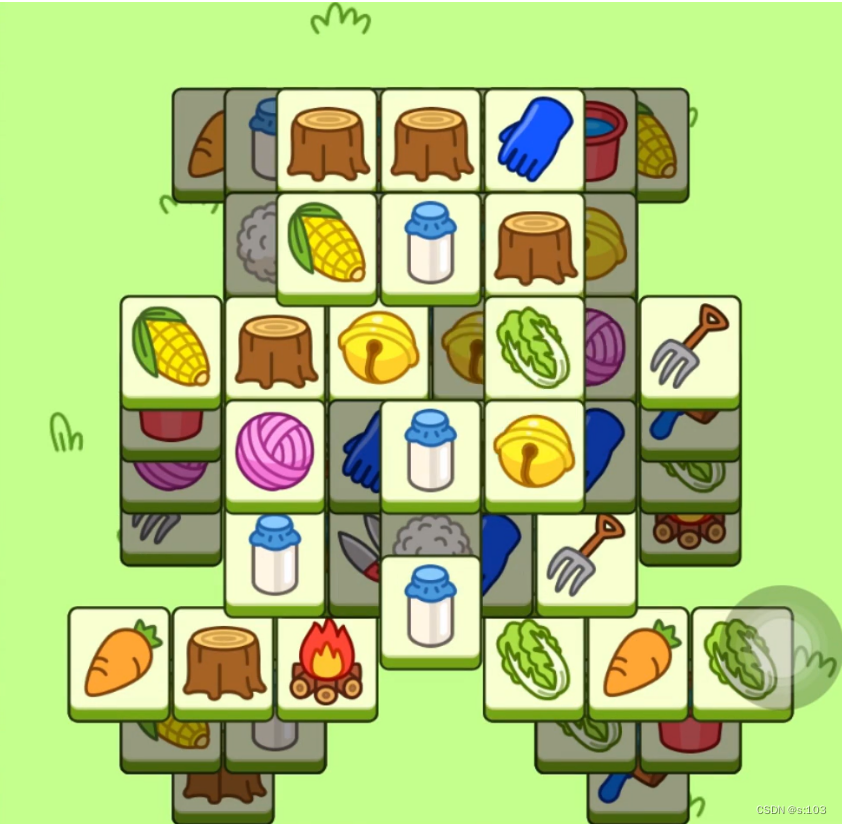
在这里插入图片描述

有一个规则：

在这里插入图片描述

当上层砖块覆盖下层砖块的时候，下层砖块不可以被选中移动（暗）
上层砖块移走后，下层砖块才能被移动（亮）

则可以用如下图表示这种逻辑结构：

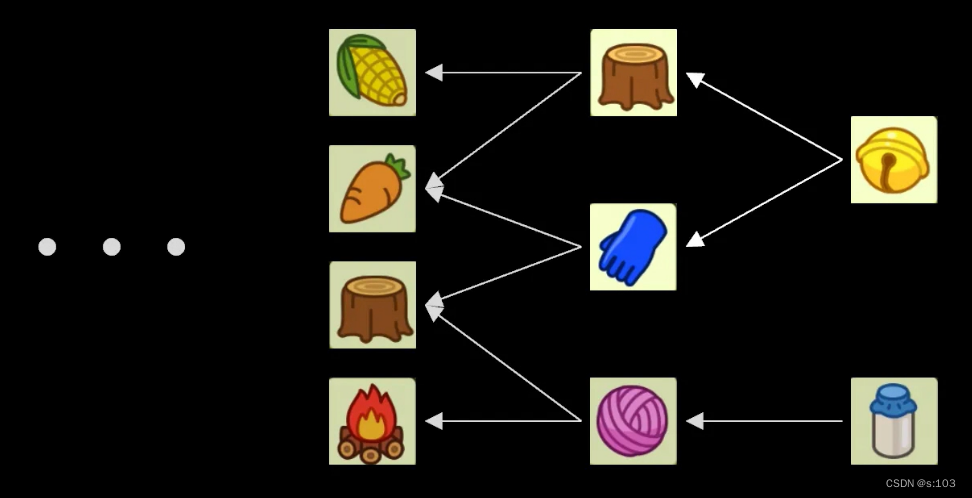
在这里插入图片描述

A->B，代表A覆盖B
即一种无环不带权有向图

带回路的话，那么这个顶点就相当于自己覆盖了自己，不合理
无向的话，一条边则是双向的，同1不合理
箭头代表覆盖关系，权值不重要

那么我们给每个砖块一个layer值：

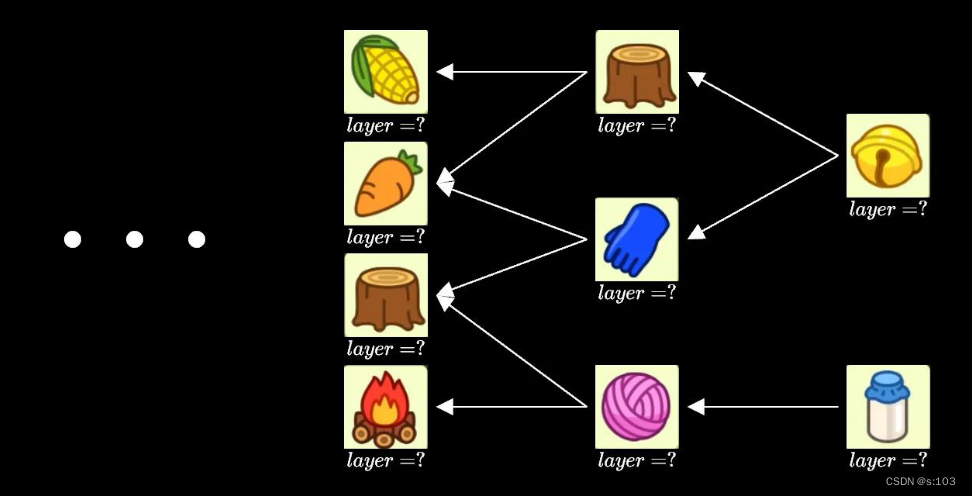
在这里插入图片描述

要求：

layer值大的砖块显示上，覆盖layer值小的砖块
即A->B，layer(A) > layer(B)

在开发过程中需要这个layer，至于用处是什么，不做解释，这里这不是重点。

至于这款游戏的原理，感兴趣的可以去网上找找资料研究一下

我们只需要找到一个序列，保证上方的覆盖者要在被覆盖者前方，再为其安排一个递减的序列

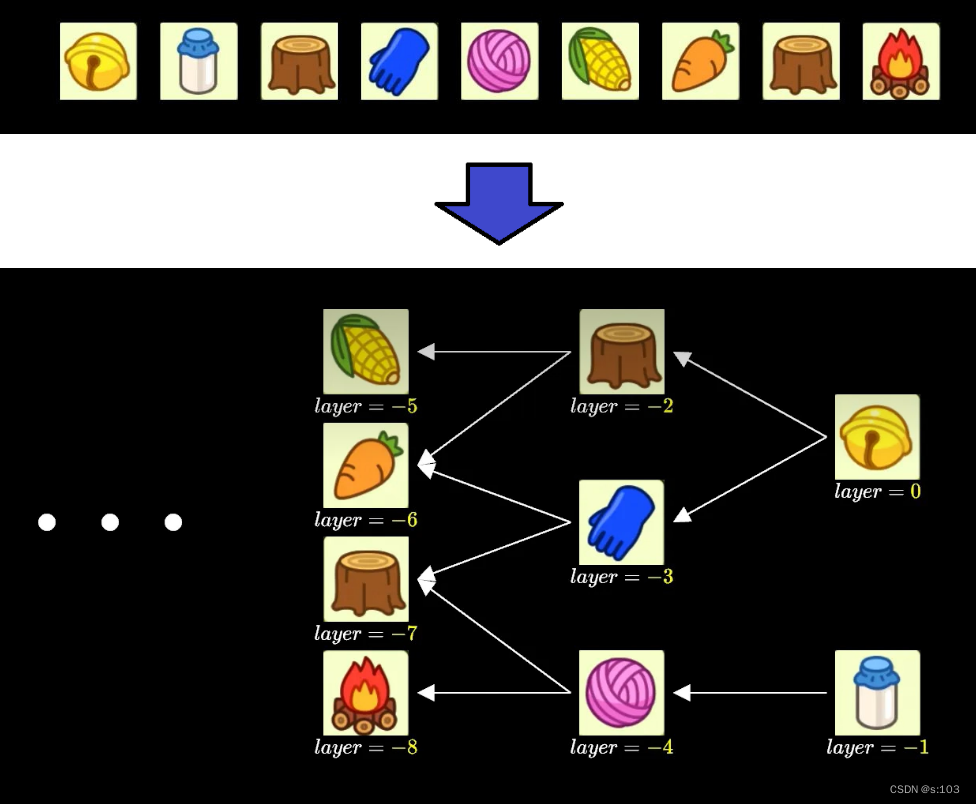
在这里插入图片描述

那么问题是：如何生成这个序列呢？

这个排序，就叫做==“拓扑排序”==

类似的，如果你需要学习一系列的课程，那么一些知识一定需要另一些知识作为基础~

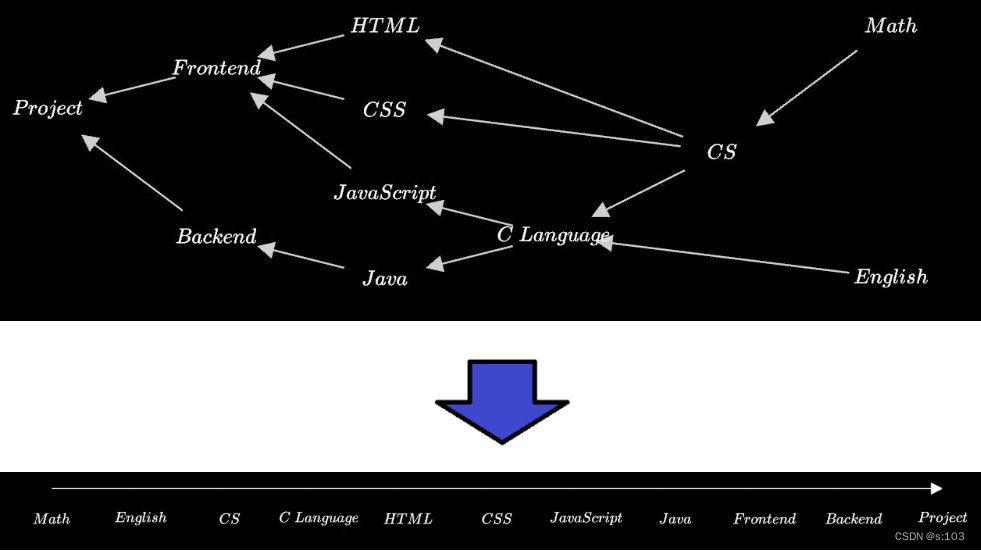
在这里插入图片描述

而显然的，符合实际的是：这种序列不应该唯一
- 学习路径肯定不一定单一呀~
事实上也如此~
- 一个图的拓扑排序很有可能有多解

2. 拓扑排序算法思想-卡恩算法

本文章用邻接表的存储结果！

基础知识传送门：Java高阶数据结构 & 图 & 图的表示与遍历_s:103的博客-CSDN博客

例子：

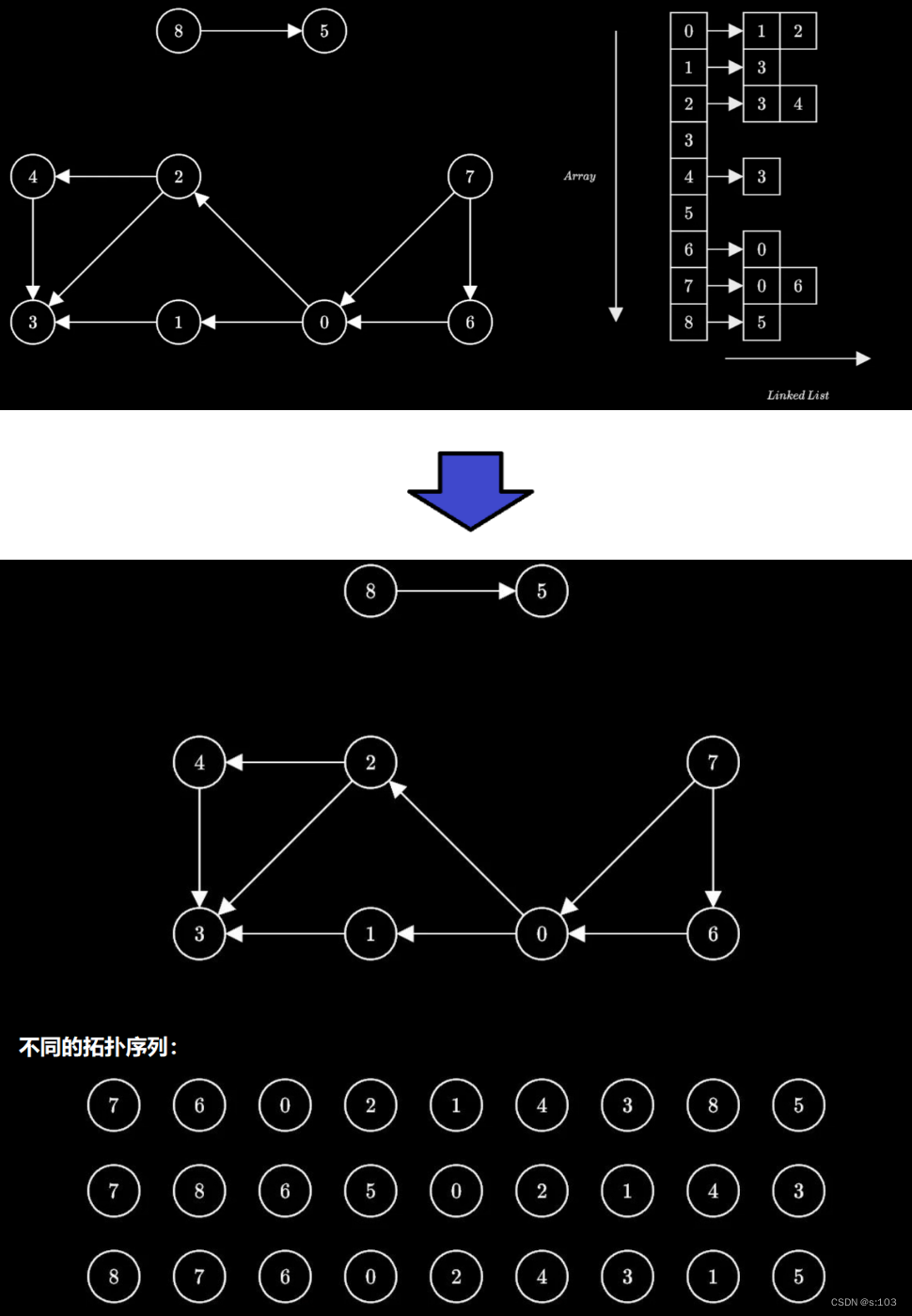
在这里插入图片描述

前面提到，如果成环则没有拓扑序列，那么我们也可以通过能否拓扑排序，来判断一个图是否带环

这也算是拓扑排序的一个额外得到功能吧

这里只讲解一种简单直接的算法，卡恩算法

重点在于每个顶点的入度

步骤：

遍历一遍邻接表，计算所有顶点的入度
挑选一个入度为0的顶点，并输出
刚才挑中的顶以及其指向的顶点的入度都减1
- -1的入度代表此顶点被删除
挑选一个入度为0的顶点，并输出
刚才挑中的顶以及其指向的顶点的入度都减1
重复这个操作，直到所有顶点都被删除（入度都为-1）
- 如果最终是因为没有入度为0的顶点而不是全部顶点都被删除而停止的循环，则说明存在环

疑问：

1. 你很快会意识到，如果出现多个入度为0的顶点，应该怎么办？

答：先挑选谁都无所谓，因为这两个入度为0的顶点，是一种并列的关系，不会相互影响。即使他们有可能分支下去会有公共顶点，这也不会导致“乱了规则”的现象，因为“汇聚的第一个公共顶点”入度至少为2，只有其入度为0的时候才能被选中

也就是说，只有如果先选中的入度为0的顶点输出后，诞生新的入度为0的顶点，一定也与原来入度为0的顶点也是并列
这也是序列不唯一的原因~

2. 为什么入度为0的顶点先被选中？

答：这很显然，入度为0，代表没人指向它

也就是说，它没被覆盖，而只覆盖别人！
万物之源

算法复杂度分析：

每个顶点和每条边都刚好被访问一次

V因为顶点数，E为边数

则时间复杂度为O(V + E)

动图演示：

在这里插入图片描述

3. 拓扑排序代码实现

我这边直接延用之前实现邻接表的代码（自制API）
获取：Java高阶数据结构 & 图 & 图的表示与遍历_s:103的博客-CSDN博客

以下代码就不做过多解释了，完全依照刚才的算法思想~

3.1 遍历链表计算入度

//获取所有顶点的入度
public int[] getDevs() {
    int n = arrayV.length;
    int[] arr = new int[n];
    for (int i = 0; i < n; i++) {
        Node cur = edgeList.get(i);
        while(cur != null) {
            arr[cur.dest]++;
            cur = cur.next;
        }
    }
    return arr;
}

3.2 挑选一个入度为0的顶点

你也可以结合isvVsted数组（标记数组）和堆去存储，节约时间
这里用最简单的遍历法

public int getFirstZero(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
        if(arr[i] == 0) {
            return i;
        }
    }
    return -1;
}

3.3 输出顶点

这里我将顶点输出到队列里了

public void outputV(int index, int[] arr, Queue<Character> queue) {
    queue.offer(arrayV[index]);
    arr[index]--;
    Node cur = edgeList.get(index);
    while(cur != null) {
        arr[cur.dest]--;
        cur = cur.next;
    }
}

3.4 判断循环结束是否为全-1

public boolean isContainCir(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
        if(arr[i] != -1) {
            return true;
        }
    }
    return false;
}

3.4 kahn方法

public static void main(String[] args) {


    //定义与构建图
    char[] chars = "012345678".toCharArray();
    GraphByList graph = new GraphByList(chars.length, true);
    graph.initArrayV(chars);
    graph.addEdge('0', '1', 1);
    graph.addEdge('0', '2', 1);
    graph.addEdge('1', '3', 1);
    graph.addEdge('2', '3', 1);
    graph.addEdge('2', '4', 1);
    graph.addEdge('4', '3', 1);
    graph.addEdge('6', '0', 1);
    graph.addEdge('7', '0', 1);
    graph.addEdge('7', '6', 1);
    graph.addEdge('8', '5', 1);

    //定义队列
    Queue<Character> queue = new LinkedList<>();
    boolean flag = graph.kahn(queue);

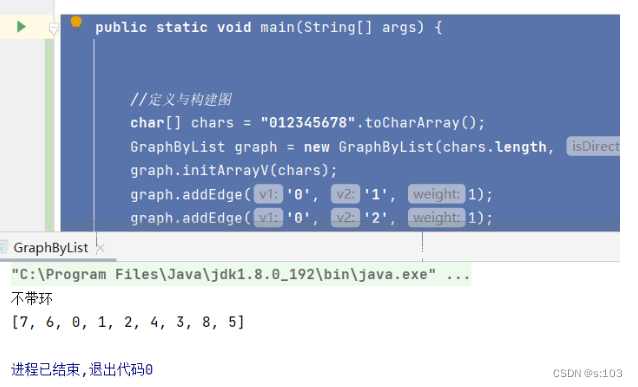
    System.out.println(flag ? "带环" : "不带环");
    System.out.println(queue);
}