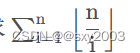特征值和特征向量问题

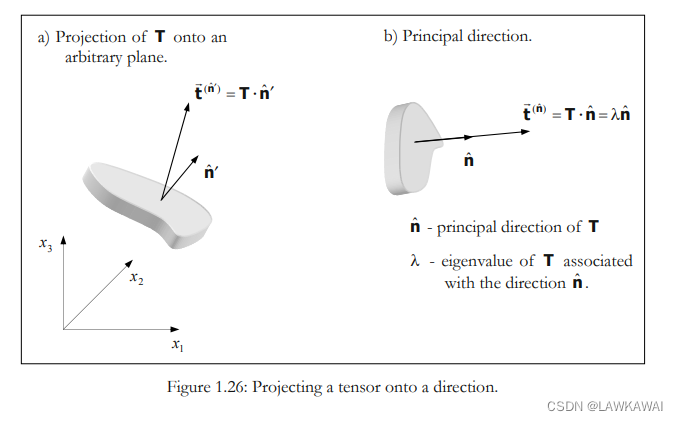
二阶张量和一个向量（单位向量${\hat{n}}^{\prime }$）的点积会得到一个向量，也就是说，将一个二阶张量投影到某个方向所得到的向量的方向实际上与${\hat{n}}^{\prime }$ 的方向不一样：

特征值和特征向量问题的目标是找到一个方向$\hat{n}$，与投影向量${\vec{t}}^{\hat{n}}=T\cdot \hat{n}$的方向一致：

$\hat{n}$是张量$T$特征向量，如果存在一个标量$\lambda$，即特征值，使得：
$$T\cdot \hat{n}=\lambda \hat{n}$$

指标形式：

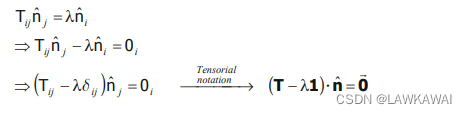
以上齐次方程只有非平凡解，例如：$\hat{n}\ne 0$ , 当且仅当：
$$\det (T-\lambda 1)=0;|T_{ij}-\lambda {\delta }_{ij}|=0$$
以上称为张量的特征行列式，显式表示为：

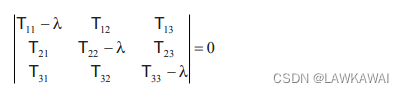
展开行列式，得到特征多项式：
$${\lambda }^3-{\lambda }^2{I}_T+\lambda I{I}_T-II{I}_T=0$$
其中，$I_t,I{I}_T,II{I}_T$是张量T的不变量：

其中$M_{ii}$是余子式矩阵的迹： $M_{ii}=M_{11}+M_{22}+M_{33}$
显式表示：

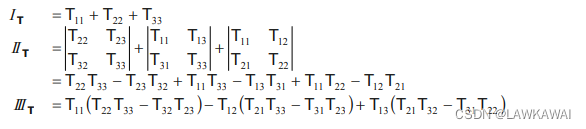
如果$T$ 是对称张量，主不变量如下：

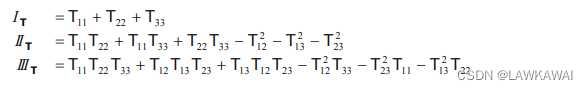
通过求解特征多项式可以得到特征值，一旦得到特征值，可以应用以下等式求出特征向量：
$(T_{ij}-{\lambda }_1{\delta }_{ij}){\hat{n}}_j^{(1)}=0_i$
$(T_{ij}-{\lambda }_2{\delta }_{ij}){\hat{n}}_j^{(2)}=0_i$
$(T_{ij}-{\lambda }_3{\delta }_{ij}){\hat{n}}_j^{(3)}=0_i$
这些特征向量构成了一个新空间，称为主空间

如果$T$是一个对称张量，那么主空间由正交基定义且所有的特征值都是实数

如果三个特征值都互不相同${\lambda }_1\ne {\lambda }_2\ne {\lambda }_3$，那么主方向是唯一的

如果其中有两个相等，${\lambda }_1={\lambda }_2\ne {\lambda }_3$，可以说明特征值${\lambda }_3$的主方向${\hat{n}}^{(3)}$是唯一的，并且任何与${\hat{n}}^{(3)}$垂直的平面是主平面，正交性是确定${\hat{n}}^{(1)}$和${\hat{n}}^{(2)}$的唯一约束

如果${\lambda }_1={\lambda }_2={\lambda }_3$，那么任何方向都是主方向

如果一个张量有3个相等特征值，那么这个张量称为球形张量

在主空间的张量分量只由主分量构成：

所以，主不变量可以表示为：
$I_T=T_1+T_2+T_3$
$I{I}_T=T_1{T}_2+T_2{T}_3+T_1{T}_3$
$II{I}_T=T_1{T}_2{T}_3$

如果$T$是球形张量，有$T_1=T_2=T_3=T，$那么主不变量为：
$I_T^2=3I{I}_T$
$II{I}_T=T^3$

如果$W$ 是一个反对称张量，$W$ 的主不变量为：

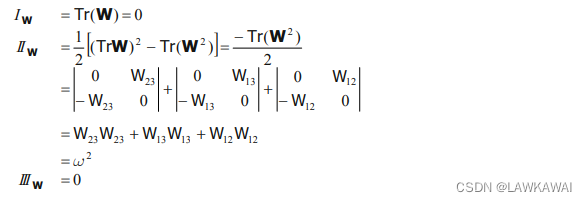
其中，$w^2=||\vec{w}|{|}^2=\vec{w}\cdot \vec{w}=W_{23}^2+W_{13}^2+W_{12}^2$，然后，反对称张量的特征方程变为：
${\lambda }^3-{\lambda }^2{I}_W+\lambda I{I}_W-II{I}_W=0⟹{\lambda }^3+w^2\lambda =0⟹\lambda ({\lambda }^2+w^2)=0$

在这种情况，有一个特征值是实数0，而其他的特征值是虚根：
${\lambda }^2+w^2=0⟹{\lambda }^2=-w^2=0⟹{\lambda }_{(1,2)}=\pm w\sqrt{-1}=\pm wi$

特征向量的正交性

若${\lambda }_1,{\lambda }_2,{\lambda }_3$是T的特征值，那么：
$T\cdot {\hat{n}}^{(1)}={\lambda }_1{\hat{n}}^{(1)}$
$T\cdot {\hat{n}}^{(2)}={\lambda }_2{\hat{n}}^{(2)}$
$T\cdot {\hat{n}}^{(3)}={\lambda }_3{\hat{n}}^{(3)}$

将${\hat{n}}^{(2)}$与 $T\cdot {\hat{n}}^{(1)}={\lambda }_1{\hat{n}}^{(1)}$ 进行点积， 并且将${\hat{n}}^{(1)}$ 与$T\cdot {\hat{n}}^{(2)}={\lambda }_2{\hat{n}}^{(2)}$ 进行点积：

$$\begin{gathered} {\hat{n}}^2\cdot T\cdot {\hat{n}}^{(1)}={\lambda }_1{\hat{n}}^{(2)}\cdot {\hat{n}}^{(1)} \\ {\hat{n}}^1\cdot T\cdot {\hat{n}}^{(2)}={\lambda }_2{\hat{n}}^{(1)}\cdot {\hat{n}}^{(2)} \end{gathered}$$

由于$T$ 是对称的，所以${\hat{n}}^2\cdot T\cdot {\hat{n}}^{(1)}={\hat{n}}^1\cdot T\cdot {\hat{n}}^{(2)}$, 所以：
$$\begin{gathered} {\lambda }_1{\hat{n}}^{(2)}\cdot {\hat{n}}^{(1)}={\lambda }_2{\hat{n}}^{(1)}\cdot {\hat{n}}^{(2)}={\lambda }_2{\hat{n}}^{(2)}\cdot {\hat{n}}^{(1)} \\ ⟹({\lambda }_1-{\lambda }_2){\hat{n}}^{(1)}\cdot {\hat{n}}^{(2)}=0 \end{gathered}$$
为了在${\lambda }_1\ne {\lambda }_2\ne 0$情况下使上面等式成立，需要：
$${\hat{n}}^{(1)}\cdot {\hat{n}}^{(2)}=0$$

同理，可得：${\hat{n}}^{(2)}\cdot {\hat{n}}^{(3)}=0{\hat{n}}^{(1)}\cdot {\hat{n}}^{(3)}=0$，则可以下结论特征向量是正交的，且构成正交基，其中坐标系之间的变换矩阵是：

对角化：

问题1.31 证明以下为不变量：$C_1^2+C_2^2+C_3^2{C}_1^3+C_2^3+C_3^3{C}_1^4+C_2^4+C_3^4$，其中$C_1,C_2,C_3$是二阶张量$C$ 的特征值

问题1.32 Q是正交张量，E是任意二阶张量，证明：E的特征值不会影响以下正交变换：$E^{\ast }=Q\cdot E\cdot Q^T$

结论：任意张量经过正交变换不改变特征值

三次方程的解

$T$是对称二阶张量，其特征方程${\lambda }^3-{\lambda }^2{I}_T+\lambda I{I}_T-II{I}_T=0$的根是都是实数，表示成：

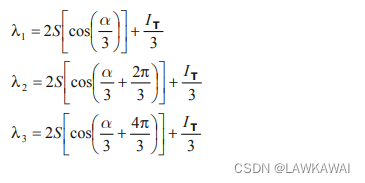
其中：

矩阵形式：

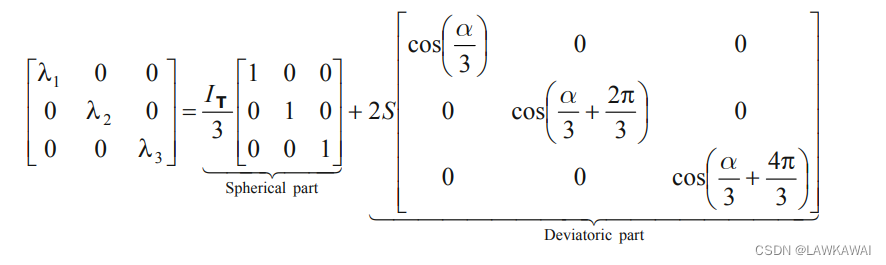
其中，我们清楚地将张量在主空间分解为球部分和偏部分
注意到，当$T$ 是一个球形张量，满足：$I_T^2=3I{I}_T$, 因此$S=0$

问题1.33 求T的主值和主方向

总结：张量的特征向量构成原坐标系$(x_1,x_2,x_3)$到主空间$(x_1^{\prime },x_2{,}^{\prime }{x}_3^{\prime })$的变换矩阵$A$

参考教材：
Eduardo W.V. Chaves， Notes On Continuum Mechanics