参考文献：《密码协议》课程 PPT

文章目录

UM & AM
- 安全定义
- 编译器
Semi-honest & Malicious
- 安全定义
- - 半诚实模型
  - 恶意模型
- 编译器
- - Input-Commitment
  - Augmented Coin-Tossing
  - Authenticated Computation
  - 编译器框架

UM & AM

安全定义

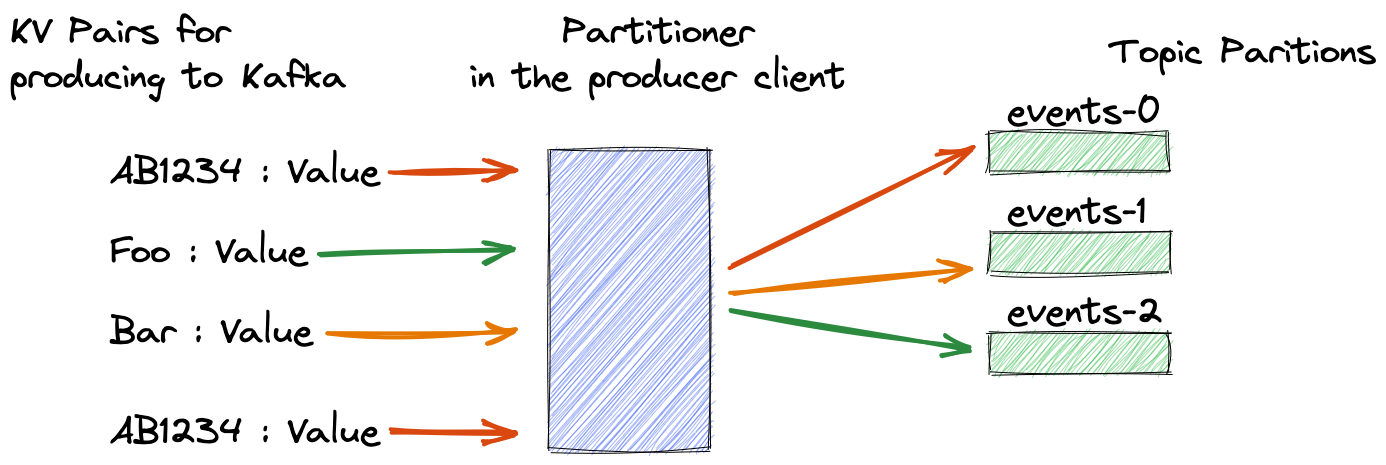
异步网络下的多方协议，它由若干会话（Session, 某协议的一份独立执行）构成。每个参与方同时与多个其他参与方执行若干个协议或者子协议的会话。每个会话被两个参与者的 $u i d$ 以及会话的 $s i d$ 唯一索引，会话执行时对应参与者会保持一个局部状态（含有私有数据），会话结束后将擦除（erase）这个状态（前向安全性（forward secrecy）：即使长期秘钥泄露，过期秘钥依然与随机秘钥不可区分），会话的输出包括数值以及事件（成功 / 失败）。环境的全局输出包括：所有参与方的局部输出、敌手的输出。

在这里插入图片描述

消息驱动（message-driven）模式：在运行环境中，进程 $P_i$ 请求执行（子）协议 $\Pi$ 时，发出 $\text{establish-session}(P_i,P_j,sid,role)$ 命令来启动协议 $\Pi$ 的一个 session，其中 $\in \{initiator, responder\}$ 。在这个 session 中， $P_i$ 将消息 $P_i,P_j,sid,message)$ 发送给 $P_j$ ，激活它在这个会话中处理此消息。

AM 敌手 $\mathcal A$ （Authenticated-Links Adversary Model）是被动的 PPT 敌手，它可以：通过其他参与方的消息来激活某个参与方（认证信道，绑定了通信两端）、任何消息至多被传递一次（异步信道，消息传递可被无限期延迟）。全局输出记为 $AUTH_{\Pi,\mathcal A}(k,\vec x,\vec r)$ ，其中 $k$ 是全局公开输入， $\vec x,\vec r$ 是各自的私有输入和随机带。

UM 敌手 $\mathcal U$ （Unauthenticated-Links Adversary Model）是主动的 PPT 敌手，它可以：操作某些会话（插入删除消息、编排执行顺序、开启结束会话）、获得某些会话的内部状态、入侵某些参与者（获取未完成会话的内部状态、查询已完成会话的秘密输出、控制信息擦除）。全局输出记为 $UNAUTH_{\Pi,\mathcal U}(k,\vec x,\vec r)$ ，其中 $k$ 是全局公开输入， $\vec x,\vec r$ 是各自的私有输入和随机带。

编译器

两个 $n$ 方的消息驱动协议 $\Pi,\Pi'$ ，我们说 $\Pi'$ 在 UM 下仿真（emulate） $\Pi$ ，如果对于任意的 UM 敌手 $U$ ，都存在 AM 敌手 $A$ ，使得
$\{AUTH_{\Pi,\mathcal A}(k,\vec x,\vec r)\}_{k,x,r} \equiv \{UNAUTH_{\Pi',\mathcal U}(k,\vec x,\vec r)\}_{k,x,r}$

这儿的 “仿真” 是说两个不同模型下的协议功能等价。

对于 AM 下的消息传递协议（message transmission, MT），可以使用签名方案，将它用某个 authenticator 转化为 UM 下功能等价的协议。

在这里插入图片描述

给定 TM 协议的编译器 $\lambda$ ，可以给出一个通用编译器 $\mathcal C_\lambda$ ：

输入任意协议 $\Pi$ 的描述
对于 $\Pi$ 的每个消息传递，协议 $\Pi'$ 都调用 $\lambda$ 来发送消息
每当 $\lambda$ 收到一个消息，协议 $\Pi'$ 用此消息来激活 $\Pi$
输出新协议 $\Pi' = \mathcal C_\lambda(\Pi)$

Semi-honest & Malicious

我们现在关注 2PC （两方安全计算）的安全性。

计算函数 $f:=(f_1,f_2)$ 的两方协议 $\Pi$ 如图所示：

在这里插入图片描述

安全定义

半诚实模型

在半诚实模型（Semi-honest Model）中，敌手是 honest-but-curious 的，它们诚实地遵照协议执行，但是会分析获得的消息序列，试图获取知识。

根据信息论，分析源数据获得的信息熵不会超过源数据本身的信息熵，因此 PPT 的敌手所获得的知识必定源于对 view 的高效计算。只要存在一个 PPT 模拟器（作为 $P_2$ 但没有 $P_2$ 的私有输入）仅根据 $P_1$ 的输入输出就模拟出 $P_1$ 的视图，则说明 $\Pi$ 的交互信息中无法高效提取出知识。

设函数 $f:\{0,1\}^* \times \{0,1\}^* \to \{0,1\}^* \times \{0,1\}^*$ 为 $f(x,y):=(f_1(x,y),f_2(x,y))$ ，协议 $\Pi$ 是计算 $f$ 的两方协议。在 $\Pi(x,y)$ 执行期间，

$P_1$ 的视图为 $View_1^\Pi(x,y) := (x,r_1,m_1,\cdots,m_t)$ ，其中 $x$ 是私有输入， $r_1$ 是内部随机带， $m_i$ 是收到的（以及发送的）消息，它的输出 $Output_1^\Pi(x,y)$ 是对 $View_1^\Pi$ 的高效计算（包含在 $View_1^\Pi$ 内）。
$P_2$ 的视图为 $View_2^\Pi(x,y) := (y,r_2,m_1,\cdots,m_s)$ ，其中 $y$ 是私有输入， $r_2$ 是内部随机带， $m_i$ 是收到的（以及发送的）消息，它的输出 $Output_2^\Pi(x,y)$ 是对 $View_2^\Pi$ 的高效计算（包含在 $View_2^\Pi$ 内）。

我们说 $\Pi$ 在 Semi-honest Model 下能够安全计算 $f$ ，

对于 $P_2$ 的安全性，存在 PPT 模拟器 $Sim_1$ （为 $P_1^*$ 模拟与 $P_2$ 的交互），使得如下的联合分布不可区分
$\{Sim_1(x,f_1(x,y)),\, f_2(x,y)\}_{X,Y} \overset{c}{\equiv} \{View_1^\Pi(x,y),Output_2^\Pi(x,y)\}_{X,Y}$
对于 $P_1$ 的安全性，存在 PPT 模拟器 $Sim_2$ （为 $P_2^*$ 模拟与 $P_1$ 的交互），使得如下的联合分布不可区分
$\{f_1(x,y),\, Sim_2(y,f_2(x,y))\}_{X,Y} \overset{c}{\equiv} \{Output_1^\Pi(x,y),\, View_2^\Pi(x,y)\}_{X,Y}$

如果 $f$ 是确定性函数，则可以简化为：
$\begin{aligned} \{Sim_1(x,f_1(x,y))\}_{X,Y} \overset{c}{\equiv} \{View_1^\Pi(x,y)\}_{X,Y}\\ \{Sim_2(y,f_2(x,y))\}_{X,Y} \overset{c}{\equiv} \{View_2^\Pi(x,y)\}_{X,Y}\\ \end{aligned}$

对于随机函数 $f$ ，联合分布是必要的。例如 $f(1^n,1^n)=(r \leftarrow_R \{0,1\}^n,\perp)$ ，我们构造 $\Pi$ 为： $P_1$ 随机掷硬币 $r$ ，将它发送给 $P_2$ ，然后 $P_1$ 输出 $r$ 但是 $P_2$ 什么也不输出。这个 $\Pi$ 根本没什么安全性可言，但是确定性版本的模拟器 $Sim_2$ 很容易构造（随机掷币 $r$ ，并随机生成 $P_2$ 的一个随机带 $\rho$ ），于是它说 $\Pi$ 安全计算了 $f$ （这太不合理了）。

恶意模型

在恶意模型（Malicious Model）中，敌手会以任意方式偏离协议：随意终止（协议执行的某一步）、改变输入值（敌手一方的）、过早停止（敌手已获得全部想要的消息，但对方仍需一些消息传递才能计算出结果）。

在 Ideal World 中存在计算 $f$ 的可信第三方（Trusted Third Party, TTP），且参与方与 TTP 之间的消息传递是不可窃听的。因此，在 Ideal World 中不存在什么敌手（即使是无界的）可以获取有关对方输入的知识。如果 Real World 中的任意敌手都可以在 Ideal World 中被模拟，就说明 Real World 中的敌手也没什么威胁。

设函数 $f:\{0,1\}^* \times \{0,1\}^* \to \{0,1\}^* \times \{0,1\}^*$ 为 $f(x,y):=(f_1(x,y),f_2(x,y))$ ，一个 admissible（可接受的）Ideal World 敌手是多项式尺寸的电路族 $C = (C_1,C_2)$ ，其中存在 $\in \{1,2\}$ 使得 $C_i(I)=I$ 且 $C_i(I,O)=O$ （人话就是：诚实方），这里 $I$ 是自己的输入， $O$ 是从 TTP 收到的输出。假设 TTP 计算 $f (x, y)$ 后首先回复 $C_1$ 然后再回复 $C_2$ （导致 $C_1^*$ 有 “早停” 的能力），那么定义 Ideal 联合执行 $Ideal_{f,C}(x,y)$ 为：

如果 $C_2$ 诚实（即 $C_2(I)=I$ 且 $C_2(I,O)=O$ ），
1. 当 $C_1(x) = \perp$ 时（ $C_1^*$ 提前终止），
  $Ideal_{f,C}(x,y) = (C_1(x,\perp),\perp)$
  
  其中 $C_1(x,\perp)$ 是收到 TTP 的回应 $\perp$ 后做的计算结果
2. 当 $C_1(x) \neq \perp$ 且 $C_1(x,f_1(C_1(x),y))=\perp$ 时（ $C_1^*$ 过早停止），
  $Ideal_{f,C}(x,y) = (C_1(x,f_1(C_1(x),y)),\perp)$
  
  其中 $C_1(x,f_1(C_1(x),y))$ 是收到 TTP 的回应 $f_1(C_1(x),y)$ 后做的计算结果
3. 对于其他情况（ $C_1$ 诚实，或者 $C_1^*$ 修改了输入），
  $Ideal_{f,C}(x,y) = (C_1(x,f_1(C_1(x),y)),f_2(C_1(x),y))$
  
  其中 $C_1(x,f_1(C_1(x),y))$ 是收到 TTP 的回应 $f_1(C_1(x),y)$ 后做的计算结果，而诚实的 $C_2$ 直接输出收到的 TTP 回应 $f_2(C_1(x),y)$
如果 $C_1$ 诚实（即 $C_1(I)=I$ 且 $C_1(I,O)=O$ ），
1. 当 $C_2(x) = \perp$ 时（ $C_2^*$ 提前终止），
  $Ideal_{f,C}(x,y) = (\perp,C_2(y,\perp))$
  
  其中 $C_2(y,\perp)$ 是收到 TTP 的回应 $\perp$ 后做的计算结果
2. 对于其他情况（ $C_2$ 诚实，或者 $C_2^*$ 修改了输入），
  $Ideal_{f,C}(x,y) = (f_1(x,C_2(y)),C_2(y,f_2(x,C_2(y))))$
  
  其中 $C_2(y,f_2(x,C_2(y)))$ 是收到 TTP 的回应 $f_2(x,C_2(y))$ 后做的计算结果，而诚实的 $C_1$ 直接输出收到的 TTP 回应 $f_1(x,C_2(y))$

设 $\Pi$ 是计算 $f$ 的两方协议，一个 admissible Real World 敌手是多项式尺寸的电路族 $C = (C_1,C_2)$ ，其中存在 $\in \{1,2\}$ 使得 $C_i$ 严格执行 $\Pi$ 所指定的策略（诚实方）。我们定义 Real 联合执行 $Real_{\Pi,C}(x,y)$ 为：交互 $\langle C_1(x),C_2(y) \rangle$ 的输出对 $Output_1^{C}(x,y),Output_2^{C}(x,y))$

我们说 $\Pi$ 在 Malicious Model 下可以安全计算 $f$ ，如果存在 PPT 变换，将 admissible poly-size real world 敌手 $A$ 转化为 admissible poly-size ideal world 敌手 $B$ ，使得
$\{Real_{\Pi,A}(x,y)\} \overset{c}{\equiv} \{Ideal_{f,B}(x,y)\}$

在恶意模型中，可以仅考虑确定性的现实敌手（概率的现实敌手，考虑最具优势的一条随机带，可以转化为确定性的）。

编译器

现在，我们将 Semi-honest 安全的协议 $\Pi$ ，转化为 Malicious 安全的协议 $\Pi'$ 。思路是：强制参与方执行半诚实行为，否则会被发现作弊行为（使用 ZKP / PoK for NPC 来约束）

约束输入：使用承诺协议（或者 OWF 等等）对输入值进行承诺，然后使用 PoK 证明自己拥有原像并且正确执行了运算（其中的随机带可以是通过 Augmented Coin-Tossing 掷出来的，如果不影响绑定性那也可以不是）
约束随机带：掷币入井（coin-tossing into the well），双方协同掷币，一方获得公平的掷币值，另一方获得此掷币值的承诺值以及对它的 PoK 证明
约束执行：对于发送的消息，使用 ZKP（不必是 PoK）来证明它是被正确计算的（先前收到的消息，以及 Augmented Coin-Tossing 和 Input-Commitment 中的承诺值）

Input-Commitment

令 $C_n:\{0,1\} \times \{0,1\}^n \to \{0,1\}^{poly(n)}$ 是（比特）承诺方案。

在恶意模型下，安全计算函数性 $f((x,r),1^n) := (\lambda,C_n(x,r))$ 的协议：

在这里插入图片描述

Augmented Coin-Tossing

令 $C_n:\{0,1\} \times \{0,1\}^n \to \{0,1\}^{poly(n)}$ 是（比特）承诺方案。

在恶意模型下，安全计算函数性 $f(1^n,1^n) := ((b,r),C_n(b,r))$ 的协议：

在这里插入图片描述

$P_1$ 与 $P_2$ 独立地执行 $1 + n$ 次掷单个公平硬币的协议： $P_1$ 掷硬币 $\sigma_i$ ，计算承诺值 $c_i$ 连同其正确执行计算的 proof 发给 $P_2$ ，然后 $P_2$ 掷硬币 $\sigma_i'$ 发送给 $P_1$ ，最后 $P_1$ 需要将 $b_0 = \sigma_0 \oplus \sigma_0'$ 作为掷硬币结果，使用 $b1\|\cdots\|b_n$ 作为随机带计算 $b_0$ 的承诺值 $c$ ，连同其正确执行计算的 proof 发送给 $P_2$

Authenticated Computation

令 $\{0,1\}^* \times \{0,1\}^* \to \{0,1\}^{poly(n)}$ 是 PPT 的函数，令 $\{0,1\}^* \times \{0,1\}^n \to \{0,1\}^{poly(n)}$ 是 PPT 的对第一个参数是 1-1 的函数（ $\forall \alpha \neq \alpha', \forall r,r',h(\alpha,r) \neq h(\alpha',r')$ ）。

在恶意模型下，安全计算函数性 $((\alpha,r,\beta),(h(\alpha,r),\beta)) \to (\lambda,f(\alpha,\beta))$ 的协议：

在这里插入图片描述

这里的 $h(\alpha,r)$ 是 $P_1$ 对输入 $\alpha$ 的承诺值（Perfect Binding），而 $f(\alpha,\beta)$ 是协议 $\Pi$ 指定的操作。

编译器框架

我们将半诚实安全的 $\Pi$ ，编译为恶意安全的 $\Pi'$ ，它分为三个阶段：

在 random-pad 阶段，双方分别执行 Augmented Coin-Tossing 获得无偏随机带。
在 input-commitment 阶段，双方分别执行 Input-Commitment 对自己的输入做承诺。
在 protocol emulation 阶段，双方利用 Authenticated Computation 来执行协议的每一步操作。
最后，如果每一步都是半诚实执行的，那么双方输出计算结果。

假设 Trapdoor OWP 存在，那么半诚实安全的 OT 协议存在。假设 OWF 存在（由 OWP 直接导致），那么承诺方案存在，ZKP 存在，对称加密算法也存在。从而通过 Garbled Circuit + OT 可以构造出半诚实安全的 2PC 协议，进一步可编译成恶意安全的 2PC 协议。