LeetCode - 34 在排序数组中查找元素的第一个和最后一个位置

news2024/11/27 6:17:28

目录

题目来源

题目描述

示例

提示

题目解析

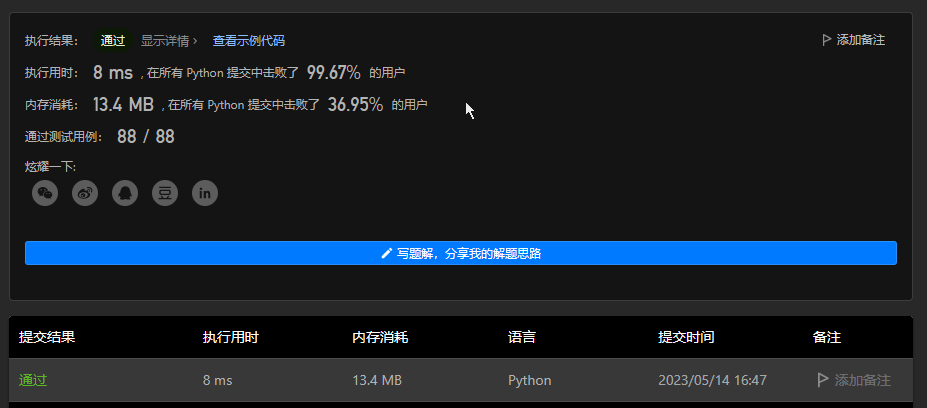
算法源码

题目来源

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

题目描述

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例

输入nums = [5,7,7,8,8,10], target = 8
输出[3,4]
说明无
输入nums = [5,7,7,8,8,10], target = 6
输出[-1,-1]
说明无
输入nums = [], target = 0
输出[-1,-1]
说明无

 

提示

  • 0 <= nums.length <= 105
  • -109 <= nums[i] <= 109
  • nums 是一个非递减数组
  • -109 <= target <= 109

题目解析

本题的nums是一个非递减顺序排列的整数数组 nums，则说明nums中是存在重复数值的，因此本题要查找的元素有第一个和最后一个位置的概念。

本题要我们在O(logN)的时间复杂度内完成元素的第一个和最后一个位置的查找，这很容易联想到二分查找，因为本题nums是一个单调的，而二分的时间复杂度也是O(logN)

但是常用的二分查找，比如Java语言的Arrays.binarySearch，并不适用于找有重复值的元素的位置，比如下面代码最终返回的要查找元素1的位置是索引2。

import java.util.Arrays;

public class Main {
  public static void main(String[] args) {
    int[] arr = {1, 1, 1, 1, 1};
    System.out.println(Arrays.binarySearch(arr, 1));
  }
}

这和底层二分查找的策略有关，关于二分查找，可以看下这篇博客中关于二分查找的实现：

算法设计 - 二分法和三分法，洛谷P3382_伏城之外的博客-CSDN博客

下面给出三种语言的标准二分查找实现

Java 标准二分查找实现

import java.util.*;
 
public class Main {
  public static void main(String[] args) {
	  int[] arr = {1,1,1,1,1};
	  System.out.println(binarySearch(arr, 1));
  }
  
  public static int binarySearch(int[] arr, int target) {
    int low = 0;
    int high = arr.length - 1;

    while (low <= high) {
      int mid = (low + high) >> 1;
      int midVal = arr[mid];

      if (midVal > target) {
        high = mid - 1;
      } else if (midVal < target) {
        low = mid + 1;
      } else {
        return mid; // midVal == target，则直接返回mid作为target的位置
      }
    }

    return -low - 1; // 找不到则返回插入位置
  }
}

JavaScript标准二分查找实现

function binarySearch(arr, target) {
  let low = 0;
  let high = arr.length - 1;

  while (low <= high) {
    const mid = (low + high) >> 1;
    const midVal = arr[mid];

    if (midVal > target) {
      high = mid - 1;
    } else if (midVal < target) {
      low = mid + 1;
    } else {
      return mid; // midVal == target，则直接返回mid作为target的位置
    }
  }

  return -low - 1; // 找不到则返回插入位置
}

Python 二分查找标准实现

def binarySearch(arr, target):
    low = 0
    high = len(arr) - 1

    while low <= high:
        mid = (low + high) >> 1
        midVal = arr[mid]

        if midVal > target:
            high = mid - 1
        elif midVal < target:
            low = mid + 1
        else:
            return mid

    return -low - 1

标准的二分查找框架中，如果midVal == target时，是直接返回了此时的mid值作为了target的位置。

但是如果target有多个重复值元素的话，那么在midVal == target时，不应该武断地判定mid就是target的位置，而是应该尝试向mid位置的左右方向进行延伸判断：

向mid位置的左边进行延伸判断：

  • 如果 mid == 0 或 arr[mid] != arr[mid-1]，则说明当前mid位置已经是 target数域 的左边界了，即target第一次出现的位置
  • 如果 mid > 0 且 arr[mid] == arr[mid - 1]，则说明target数域的左边界还在mid位置的左边，此时为了找到左边界，我们应该让 high = mid - 1

向mid位置右边进行延伸判断：

  • 如果 mid == arr.length - 1 或者 arr[mid] != arr[mid + 1]，则说明按当前mid位置已经是 target数域 的右边界了，即target最后一次出现的位置
  • 如果 mid < nums.length -1 且 arr[mid] == arr[mid+1]，则说明target数域的右边界还在mid位置的右边，此时为了找到右边界，我们应该让 low = mid + 1

实现代码如下：

Java实现代码

import java.util.*;
 
public class Main {
  public static void main(String[] args) {
	  int[] arr = {1,1,1,1,1};
	  System.out.println(binarySearch(arr, 1));
  }
  
  public static int searchFirst(int[] arr, int target) {
    int low = 0;
    int high = arr.length - 1;

    while (low <= high) {
      int mid = (low + high) >> 1;
      int midVal = arr[mid];

      if (midVal > target) {
        high = mid - 1;
      } else if (midVal < target) {
        low = mid + 1;
      } else {
		// 向左延伸判断，mid是否为target数域的左边界，即第一次出现的位置
		if(mid == 0 || arr[mid] != arr[mid - 1]) {
			return mid;
		} else {
			high = mid - 1;
		}
      }
    }

    return -low - 1; // 找不到则返回插入位置
  }
  
  public static int searchLast(int[] arr, int target) {
    int low = 0;
    int high = arr.length - 1;

    while (low <= high) {
      int mid = (low + high) >> 1;
      int midVal = arr[mid];

      if (midVal > target) {
        high = mid - 1;
      } else if (midVal < target) {
        low = mid + 1;
      } else {
		// 向右延伸判断，mid是否为target数域的右边界，即最后一次出现的位置
		if(mid == nums.length - 1 || arr[mid] != arr[mid + 1]) {
			return mid;
		} else {
			low = mid + 1;
		}
      }
    }

    return -low - 1; // 找不到则返回插入位置
  }
}

JavaScript实现代码

function searchFirst(arr, target) {
  let low = 0;
  let high = arr.length - 1;

  while (low <= high) {
    const mid = (low + high) >> 1;
    const midVal = arr[mid];

    if (midVal > target) {
      high = mid - 1;
    } else if (midVal < target) {
      low = mid + 1;
    } else {
      // 向左延伸判断，mid是否为target数域的左边界，即第一次出现的位置
      if (mid == 0 || arr[mid] != arr[mid - 1]) {
        return mid;
      } else {
        high = mid - 1;
      }
    }
  }

  return -low - 1; // 找不到则返回插入位置
}

function searchLast(arr, target) {
  let low = 0;
  let high = arr.length - 1;

  while (low <= high) {
    const mid = (low + high) >> 1;
    const midVal = arr[mid];

    if (midVal > target) {
      high = mid - 1;
    } else if (midVal < target) {
      low = mid + 1;
    } else {
      // 向右延伸判断，mid是否为target数域的右边界，即最后一次出现的位置
      if (mid == arr.length - 1 || arr[mid] != arr[mid + 1]) {
        return mid;
      } else {
        low = mid + 1;
      }
    }
  }

  return -low - 1; // 找不到则返回插入位置
}

Python实现代码

def searchFirst(arr, target):
    low = 0
    high = len(arr) - 1

    while low <= high:
        mid = (low + high) >> 1
        midVal = arr[mid]

        if midVal > target:
            high = mid - 1
        elif midVal < target:
            low = mid + 1
        else:
            if mid == 0 or arr[mid] != arr[mid - 1]:
                return mid
            else:
                high = mid - 1

    return -low - 1


def searchLast(arr, target):
    low = 0
    high = len(arr) - 1

    while low <= high:
        mid = (low + high) >> 1
        midVal = arr[mid]

        if midVal > target:
            high = mid - 1
        elif midVal < target:
            low = mid + 1
        else:
            if mid == len(arr) - 1 or arr[mid] != arr[mid + 1]:
                return mid
            else:
                low = mid + 1

    return -low - 1

Java算法源码

class Solution {
    public int[] searchRange(int[] nums, int target) {
        return new int[]{search(nums, target, true), search(nums, target, false)};
    }

    public int search(int[] nums, int target, boolean isFirst) {
        int low = 0;
        int high = nums.length - 1;

        while(low <= high) {
            int mid = (low + high) >> 1;
            int midVal = nums[mid];

            if(midVal > target) {
                high = mid - 1;
            } else if(midVal < target) {
                low = mid + 1;
            } else {
                if(isFirst) {
                    // 查找元素的第一个位置
                    if(mid == 0 || nums[mid] != nums[mid-1]){
                        return mid;
                    } else {
                        high = mid - 1;
                    }
                } else {
                    // 查找元素的最后一个位置
                    if(mid == nums.length - 1 || nums[mid] != nums[mid + 1]) {
                        return mid;
                    } else {
                        low = mid + 1;
                    }
                }
                
            }
        }

        return -1;
    }
}

 

JavaScript算法源码

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
var searchRange = function(nums, target) {
    function search(nums, target, isFirst) {
        let low = 0;
        let high = nums.length - 1;

        while(low <= high) {
            const mid = (low + high) >> 1;
            const midVal = nums[mid];

            if(midVal > target) {
                high = mid - 1;
            } else if(midVal < target) {
                low = mid + 1;
            } else {
                if(isFirst) {
                    if(mid == 0 || nums[mid] != nums[mid-1]) {
                        return mid;
                    } else {
                        high = mid - 1;
                    }
                } else {
                    if(mid == nums.length - 1 || nums[mid] != nums[mid + 1]) {
                        return mid;
                    } else {
                        low = mid + 1;
                    }
                }
            }
        }

        return -1;
    }

    return [search(nums, target, true), search(nums, target, false)];
};

 

Python算法源码

class Solution(object):
    def searchRange(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        return self.search(nums, target, True), self.search(nums, target, False)
    
    def search(self, nums, target, isFirst):
        low = 0
        high = len(nums) - 1

        while low <= high:
            mid = (low + high) >> 1
            midVal = nums[mid]

            if midVal > target:
                high = mid - 1
            elif midVal < target:
                low = mid + 1
            else:
                if isFirst:
                    if mid == 0 or nums[mid] != nums[mid-1]:
                        return mid
                    else:
                        high = mid - 1
                else:
                    if mid == len(nums) - 1 or nums[mid] != nums[mid + 1]:
                        return mid
                    else:
                        low = mid + 1
        
        return -1

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/524976.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【项目笔记】若干基本社团发现算法介绍

【项目笔记】若干基本社团发现算法介绍

两个衡量指标&#xff1a;边介数 & 模块度 边介数计算&#xff1a; 以下用图来自&#xff1a;https://blog.csdn.net/weixin_44704845/article/details/102686597 选择S为源节点对图搜索&#xff0c;画出S到其他节点的最短路径树 2.给边标数字 1&#xff09; 所有邻近叶…
阅读更多...
【YOLO系列】--YOLOv4超详细解读/总结（网络结构）

【YOLO系列】--YOLOv4超详细解读/总结（网络结构）

YOLOv4&#xff08;YOLOv4: Optimal Speed and Accuracy of Object Detection&#xff09;&#xff08;原文&#xff0b;解读/总结&#xff0b;翻译&#xff09; 系列文章&#xff1a; YOLOv1论文解读/总结_yolo论文原文_耿鬼喝椰汁的博客-CSDN博客 YOLOv2论文解读/总结_耿鬼…
阅读更多...
软件测试面试至今0 offer，问题到底出在哪儿？

软件测试面试至今0 offer，问题到底出在哪儿？

转眼已是四月中旬&#xff0c;求职招聘季也快要结束啦&#xff0c;如果没点真技术 真本事&#xff0c;不了解点职场套路&#xff0c;在今年行情下&#xff0c;找工作可是难上加难。 现在点开微博或者脉脉&#xff0c;只要搜索“招聘”&#xff0c;用“惨不忍睹”来形容也不为过…
阅读更多...
【数据结构】经典排序

【数据结构】经典排序

【数据结构】八大排序 1. 排序的概念和运用1.1 概念1.2 运用 2. 常规的排序算法介绍一. 插入排序1.1 直接插入排序1.2 希尔排序 二. 选择排序2.1 选择排序2.2 堆排序 三. 交换排序3.1 冒泡排序3.2 快速排序3.2.1 Hoare法3.2.2 挖坑法3.2.3 前后指针/左右指针法3.2.4 分治法/递归…
阅读更多...
windows11 安装 webassembly,遇到的各种错误

windows11 安装 webassembly,遇到的各种错误

1.最开始是尝试在 虚拟机 centos 7 安装的(因为不想安装vs2015) 但是无奈 各种错误.最终无法解决. 2.尝试在windows安装,吐槽一下官方文档 的安装提示是错误的(太老了) 参考以下文章: https://blog.csdn.net/weixin_45482422/article/details/119459918 https://blog.csdn.…
阅读更多...
C++中this指针的特性，存放位置，能否为空？

C++中this指针的特性，存放位置，能否为空？

文章目录 一、this指针的特性二、this指针存在哪里&#xff1f;三、this指针可以为空吗&#xff1f; 一、this指针的特性 我们学习过C知道&#xff0c;成员函数没有直接存放在类而是放在了公共代码区&#xff0c;这样当多个对象调用同一个函数就不需要再创建一个函数成员了。 …
阅读更多...
libevent高并发网络编程 - 02_libevent缓冲IO之bufferevent

libevent高并发网络编程 - 02_libevent缓冲IO之bufferevent

文章目录 1. 为什么需要缓冲区&#xff1f;2. 水位3. bufferevent常用API3.1 evconnlistener_new_bind()3.2 evconnlistener_free()3.3 bufferevent_socket_new()3.4 bufferevent_enable()3.5 bufferevent_set_timeouts()3.6 bufferevent_setcb()3.7 bufferevent_setwatermark(…
阅读更多...
全面解析Linux指令和权限管理

全面解析Linux指令和权限管理

目录 一.指令再讲解1.时间相关的指令2.find等搜索指令与grep指令3.打包和压缩相关的指令4.一些其他指令与热键二.Linux权限1.Linux的权限管理2.文件类型与权限设置3.目录的权限与粘滞位 一.指令再讲解 1.时间相关的指令 date指令: date 用法&#xff1a;date [OPTION]… [FOR…
阅读更多...
缓冲区的flip

缓冲区的flip

流和缓冲区都是用来描述数据的。计算机中&#xff0c;数据往往会被抽象成流&#xff0c;然后传输。比如读取一个文件&#xff0c;数据会被抽象成文件流&#xff1b;播放一个视频&#xff0c;视频被抽象成视频流。处理节点为了防止过载&#xff0c;又会使用缓冲区削峰&#xff0…
阅读更多...
巴西大神开发的 ARPL 黑群晖DSM系统引导在线编译工具

巴西大神开发的 ARPL 黑群晖DSM系统引导在线编译工具

ARPL 是一款黑群晖系统引导在线编译工具&#xff0c;目前支持最新群晖系统DSM 7.1.1&#xff0c;今天为了折腾升级这个群晖系统DSM 7.1.1浪费了一天的时间&#xff0c;ARPL是巴西人一位大神开发的黑群晖系统引导在线编译工具&#xff0c;使用下来非常的不错&#xff0c;可惜没有…
阅读更多...
3网络互联-3.4【实验】【计算机网络】

3网络互联-3.4【实验】【计算机网络】

3网络互联-3.4【实验】【计算机网络】 前言推荐3网络互联3.4 IP分组转发与静态路由实验目的实验内容及实验环境实验原理1.路由器2.路由(Routing)3.IP分组的转发4.路由的构建5.静态路由设计原则 实验过程1&#xff0e;搭建一个仅包含直连路由的网络拓扑&#xff0c;观察路由器的…
阅读更多...
时间序列分析

时间序列分析

一、移动平均法 1.一次移动平均法 公式&#xff1a; 预测标准误差: 本质&#xff1a;用前N次数据预测t1期的数据 规律&#xff1a;如果实际数据波动较大&#xff0c;N值越大&#xff0c;预测到的数据波动越小 注意&#xff1a;一般不适用于波动较大的数据。用一次移动平均法…
阅读更多...
Kafka原理之消费者

Kafka原理之消费者

一、消费模式 1、pull(拉)模式(kafka采用这种方式) consumer采用从broker中主动拉取数据。 存在问题&#xff1a;如果kafka中没有数据&#xff0c;消费者可能会陷入循环中&#xff0c;一直返回空数据 2、push(推)模式 由broker决定消息发送频率&#xff0c;很难适应所有消费者…
阅读更多...
【MySQL】 InnoDB

【MySQL】 InnoDB

学习笔记&#xff0c;来源黑马程序员MySQL教程 文章目录 逻辑存储结构架构内存架构磁盘结构后台线程 事务原理概述redo logundo log MVCC基本概念实现原理1、隐藏字段2、undo log3、readview 总结 逻辑存储结构 一个表空间对应一张表一 页 对应B树上一个 节点Trx id&#xff1a…
阅读更多...
Git cat命令的用法

Git cat命令的用法

cat (全称 concatenate) 命令是 Linux/类 Unix 操作系统中最常用的命令之一。cat 命令允许我们创建单个或多个文件、查看文件内容、连接文件和重定向终端或文件中的输出。 语法&#xff1a; cat [OPTION] [FILE]...1.终端查看一个文件内容 cat file01.txt2.终端查看多个文件…
阅读更多...
熵、信息量、条件熵、联合熵、互信息简单介绍

熵、信息量、条件熵、联合熵、互信息简单介绍

熵、信息量、条件熵、联合熵、互信息简单介绍 近期在看对比学习论文&#xff0c;发现有不少方法使用了互信息这种方式进行约束&#xff0c;故在此整理一下网上查阅到的关于互信息的相关内容。 一、熵、信息量 关于熵的讨论&#xff0c;这个知乎专栏写的挺不错的。 熵在信息论…
阅读更多...
【更新日志】填鸭表单TduckPro v5.1 更新

【更新日志】填鸭表单TduckPro v5.1 更新

hi&#xff0c;各位Tducker小伙伴。 填鸭表单pro迎来了v5.1版本&#xff1b;本次我们进行了许多的功能新增和优化&#xff0c;能够让我们在日常使用中获得更好的体验。 让我们一起来康康新功能吧。 01 新增Pro功能 新增登录后才能填写表单。 新增表单卡片一键发布。 新增矩…
阅读更多...
【C++学习】CC++内存管理

【C++学习】CC++内存管理

目录 一、C&C内存管理 二、C语言中动态内存管理方式&#xff1a;malloc/calloc/realloc/free 三、C内存管理方式 3.1 new/delete操作内置类型 3.2 new和delete操作符自定义类型 四、operator new与operator delete函数 4.1 operator new与operator delete函数&#x…
阅读更多...
【云原生】使用外网Rancher2.5.12在阿里云自建内网K8s 1.20集群

【云原生】使用外网Rancher2.5.12在阿里云自建内网K8s 1.20集群

目录 一、目标二、解决方案三、草图四、版本信息五、资源规划六、必要条件七、开始部署1、安装Docker2、安装Rancher3、解析Rancher Server URL域名4、创建K8s集群5、注册K8s集群节点 八、验证 一、目标 在云平台搭建一套高可用的K8s集群 二、解决方案 第一种&#xff1a;使…
阅读更多...
横向移动-利用IPC$

横向移动-利用IPC$

环境主机 本次都是在内网自己搭的靶机实验 上线主机&#xff1a;windows2008R2 - 192.168.31.46 需要移动到的主机&#xff1a;windows2012 - 192.168.31.45 实验演示 1.确定域控 通过命令net time /domain&#xff0c;发现存在域 这里我们通过ping来发现域控的ip&#xff0c;…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023