熵、信息量、条件熵、联合熵、互信息简单介绍

近期在看对比学习论文，发现有不少方法使用了互信息这种方式进行约束，故在此整理一下网上查阅到的关于互信息的相关内容。

一、熵、信息量

关于熵的讨论，这个知乎专栏写的挺不错的。

熵在信息论中代表随机变量不确定度的度量，变量不确定性越大，信息熵也就越大。一个离散型随机变量$X$的熵$H(X)$定义为：

$$H(X)=-\sum _{x\in \chi }p(x)logp(x)$$

其中$p(x)$表示$x$发生的概率。从公式不难发现，信息熵$H(x)$满足当$x$的确定时即$p(x)=1$时最小，当$x$为均匀分布时即$p(x)=\frac{1}{n}$时最大。这也就意味着，事件越不确定，熵越大。此外，该公式还满足以下三个性质：

• 单调性，即发生概率越高的事件，其所携带的信息熵越低。极端案例就是“太阳从东方升起”，因为为确定事件，所以不携带任何信息量。从信息论的角度，认为这句话没有消除任何不确定性。
• 非负性，即信息熵不能为负。这个很好理解，因为负的信息，即你得知了某个信息后，却增加了不确定性是不合逻辑的。
• 累加性，即多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和。写成公式就是：$H(A,B)=H(A)+H(B)-I(A,B)$，其中$I(A,B)$就是互信息。

不难发现，上述几个性质恰好就是我们想要获得的计算熵公式。通过数学证明发现满足上述性质的公式只有：$H(X)=-C{\sum }_{x\in \chi }p(x)logp(x)$。

信息熵不等同于信息量，但它们在量上是相等的。 即，“熵”度量了不确定性，而接受信息后所消除的不确定性即为该信息的“量”。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SBnmQw2m-1684065604452)(D:\研究生文件\顶会顶刊论文代码\笔记\图片\image-20230514173305337.png)]

二、条件熵、联合熵

条件熵的概念是$X$给定的情况下，$Y$的条件概率分布的熵对$X$的期望。公式如下：

$$H(Y|X)=\sum _{x\in \chi }p(x)H(Y|X=x)=-\sum _{x\in \chi }p(x)\sum _{y\in Y}p(y|x)logp(y|x)=-\sum _{x\in \chi }\sum _{y\in Y}p(x,y)logp(y|x)$$

注意这里是期望，加了求和号的。也就是对于$X$的所有取值都要考虑。条件熵的物理意义是在得知某一确定信息的基础上获取另外一个信息时所获得的信息量。

联合熵不多解释直接上公式，如下:

$$H(X,Y)=-\sum _{x\in \chi }\sum _{y\in Y}p(x,y)logp(x,y)$$

联合熵的物理意义就是，观察一个多个随机变量的随机系统获得的信息量。

好了，公式给出来了，不难发现联合熵和条件熵的关系如下：

$H(X,Y)=H(X)+H(Y|X)$

这个所表达的物理含义是，对一个两个随机变量的随机系统，我们可以先观察一个随机变量获取信息量，观察完后，我们可以在拥有这个信息量的基础上观察第二个随机变量的信息量。先观察谁，对信息量都不会有影响。

三、互信息

关于互信息这篇博客写的挺不错的，下面是博客截图：

由

可得出互信息与其它量的关系如下：

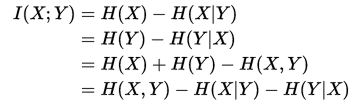
好了，回到对比学习中。我们知道对比学习的常见做法是取一个Batchsize中的$N$张图片，对其进行数据增强如平移、旋转等获得$2N$张图片。任取其中一张图片$X$，则令其对应经过数据增强获得的图片$Y$为正样本、其余$2N-2$张图片为负样本。之后利用损失函数进行约束即可训练网络。

那么，这东西和互信息有啥关系呢。试想一下，如果$I(X,Y)=maxI(X,Y)$是不是就是意味着$X$能够直接确定$Y$。这不就是对比学习想要干的事情。