两个衡量指标:边介数 & 模块度
边介数计算:
以下用图来自:https://blog.csdn.net/weixin_44704845/article/details/102686597
- 选择S为源节点对图搜索,画出S到其他节点的最短路径树
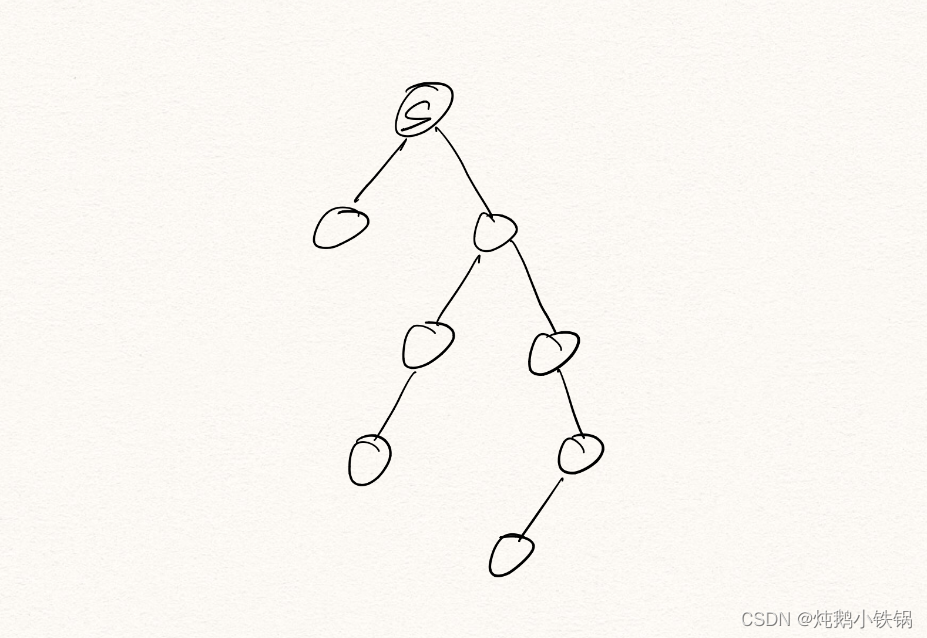
2.给边标数字
1) 所有邻近叶子结点的那条边标上1
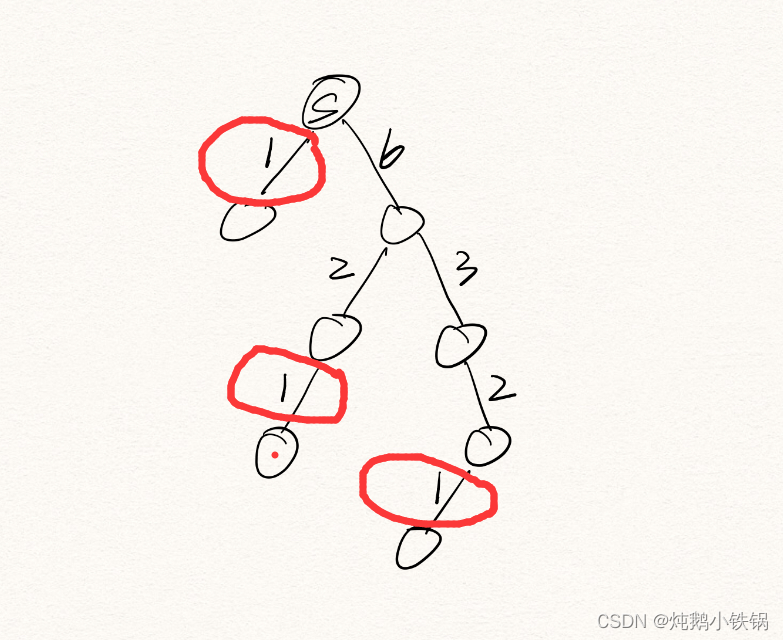
2)再给其他边标上所有最邻近他的边之和+1
获得S作为源节点时的各边单次边介数
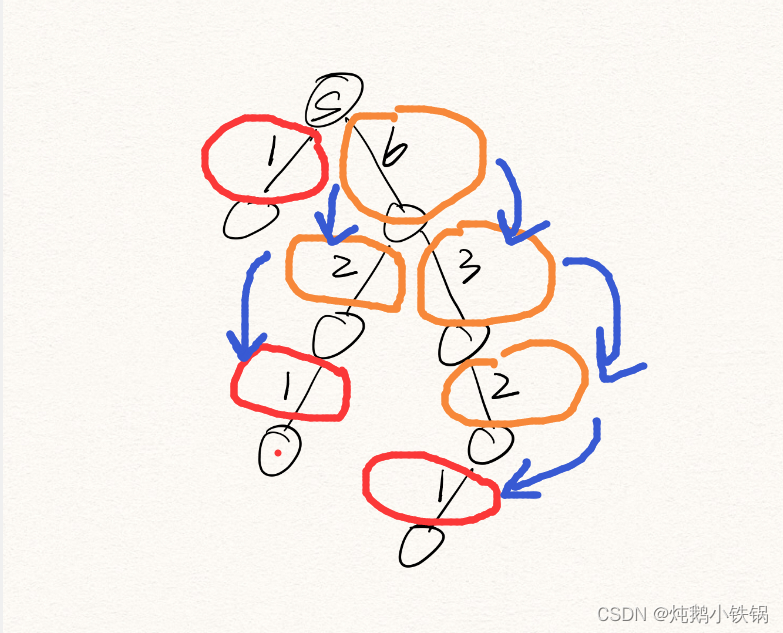
3.然后再换一个节点作为边节点(根?)
相同方法计算边标数,当遍历完所有节点后,将各边的的单次边介数累计求和,得到的最终该边边介数
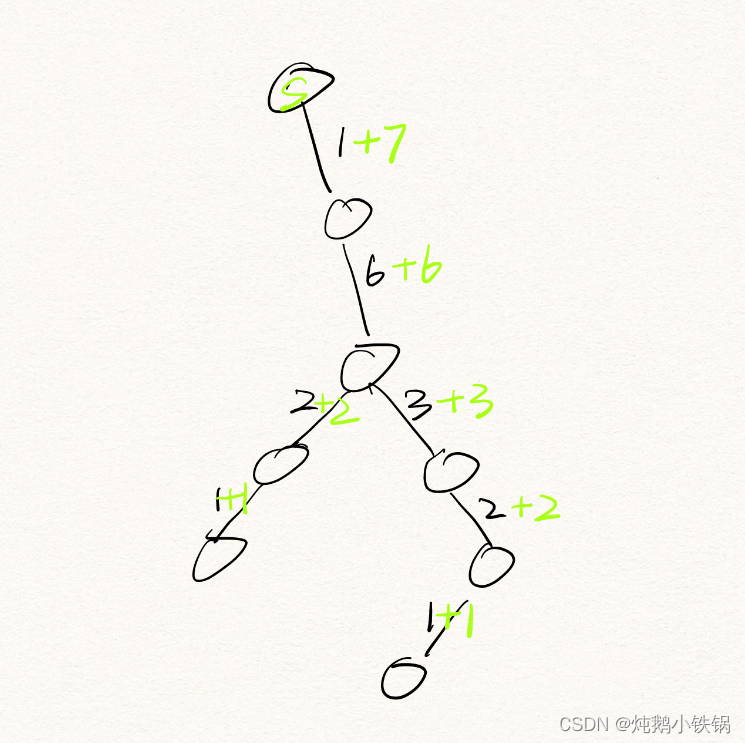
边介数概念理解
Definition:从源节点S到各节点最短路径中,经过该边的路径数
- 源节点S到各节点都只有一条最短路径
- 橙色边单次边介数为2,经过它的最短路径有2条
- 蓝色边单次边介数为6,经过它的最短路径有6条
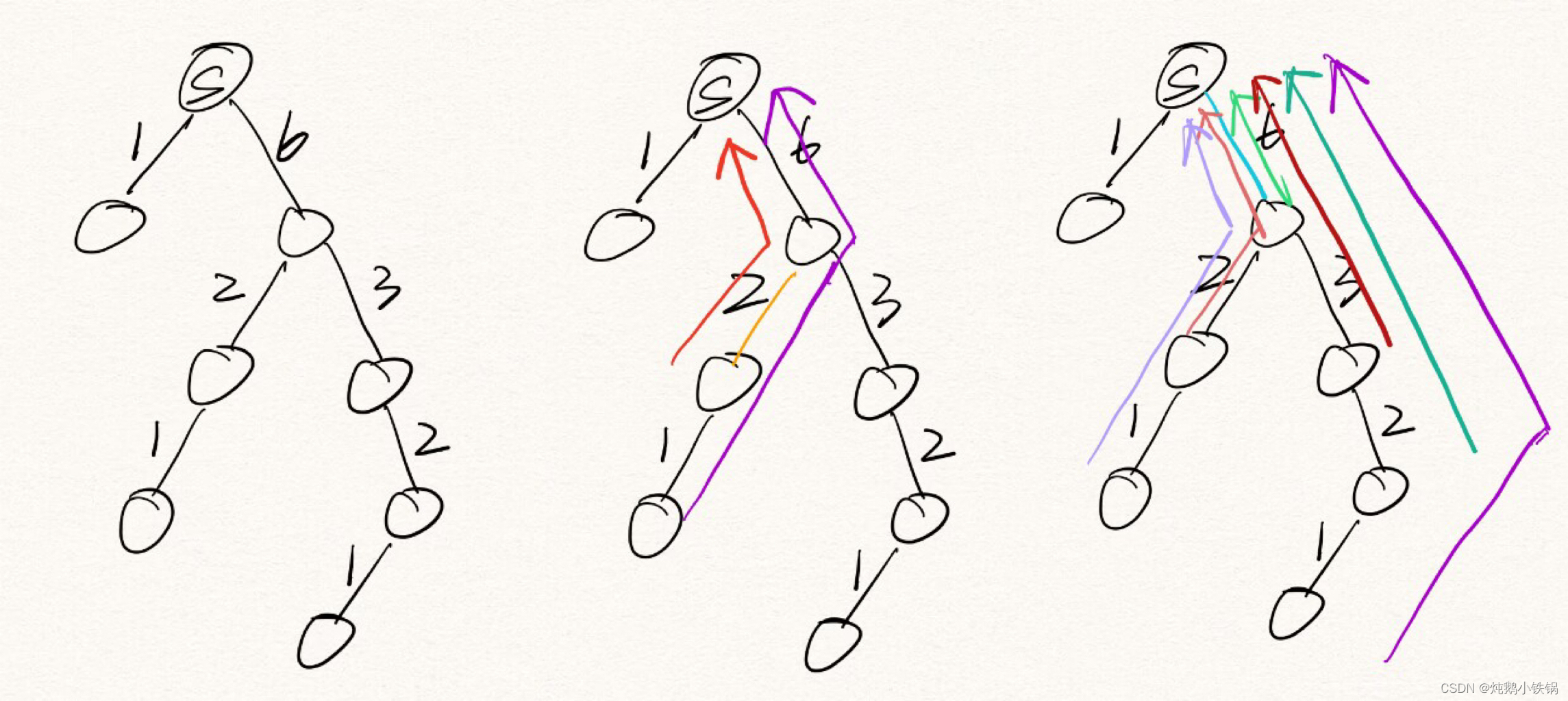
总结:社团内部的边边介数小,社团之间的边边介数大。
模块度Q:
Q值计算: (社区内部的总边数 / 网络中总边数) - K
- K是一个期望值
- K = 将网络设定为随机网络时,同样的社团数量分配,形成的: (社区内部的总边数 / 网络中总边数)
Q值物理含义:网络中:E[社区内部的边的占比 - 在同样的社区结构下任意连接节点的边的占比] (E是求期望)
- 如果社区内部边的比例不大于任意连接时的期望值(找到的社团还没有随意连接的网络中形成的社团质量好),则Q=0。
- Q∈[0,1],数值越大,社区结构越明显。实际网络中,该值通常位于0.3-0.7之间。
基于模块度的GN算法
- 计算当前网络的边介数和模块度Q值,并存储模块度Q值和当前网络的社团分割情况;
- 除去边介数最高的边(社团之间的边);
- 计算当前网络的模块度Q值,如果此Q值比原来的大,则将现在的Q值和网络中社团分割情况存储更新,否则,进行下一次网络分割;
- 所有边分割完毕,返回当前的模块度Q值和社团分割情况。
Newman快速算法 (FN算法)
- 将网络中的每个顶点设为一个单独社区,
- 每次迭代选择产生最大Q值的两个社团合并,直至整个网络融合成一个社团。
- 整个过程是自底向上的过程
- 这个过程最终得到一个树图,
- 树的叶子节点表示网络中的顶点,树的每一层切分对应着网络的某个具体划分
- 从树图的所有层次划分中选择模块度值最大的划分作为社团划分。
具体实现:
- 设网络有n个节点,m条边
- 每一步的社区数目为 r,组成一个 r×r 矩阵 e
- 矩阵元素eij表示两个社团 i 和 j 中,社团内节点之间连边的数目 占网络中总边数的百分比
(1)初始化网络,开始网络有n 个社区,初始化的eij 和 ai
(2)依次按照∆Q的最大或者最小的方向进行合并有边相连的社区对,并计算合并后的模块度增量∆Q
(3)修改矩阵e
(4)重复执行步骤(2)和(3),直至整个网络合并成一个社区
Louvain 算法
- 将每个节点指定到唯一的一个社区
- 然后按顺序将节点在这些社区间进行移动
- 假设有一节点 i ,它有三个邻居节点 j1, j2, j3,分别尝试将节点 i 移动到 j1, j2, j3 所在的社区,并计算相应的模块度变化值ΔQ
- 选择ΔQ最大,将节点 i 移动到相应的社区中去(ΔQ要为正,如果变化值均为负,则节点 i 保持不动)。
- 按照贪心ΔQ反复迭代,直到网络中任何节点的移动都不能增大总模块度