目录
引言:
学习:
代码实现:
头文件(Chain_Stack.h):
设置链栈中的元素范型:
链栈的结构体设计:
所有功能函数的声明:
源文件(Chain_Stack.cpp)对函数功能的具体实现:
初始化函数(Init_Stack):
清空函数(Clear);
销毁函数(Destroy):
打印函数(Show):
查找函数(Search):
入栈函数(Push):
出栈函数(Pop):
返回栈顶元素函数(Top):
判空函数(IsEmpty):
获取有效数据个数函数(Get_Length):
测试:
测试初始化函数、打印函数:
测试清空函数:
测试销毁函数:
测试查找函数:
测试入栈函数:
测试出栈函数:
测试返回栈顶元素函数:
引言:
数据结构学习目录:
数据结构系列学习(一) - An Introduction to Data Structure
数据结构系列学习(二) - 顺序表(Contiguous_List)
数据结构系列学习(三) - 单链表(Linked_List)
数据结构系列学习(四) - 单向循环链表(Circular Linked List)
数据结构系列学习(五) - 双向链表(Double_Linked_List)
数据结构系列学习(六) - 顺序栈(Stack)
在上篇文章中我们了解学习了顺序栈,并使用代码对它进行了实现。这篇文章我们将对栈的另外一种表达形式——链栈(Chain_Stack)进行了解学习并使用代码对它进行实现。
学习:
链栈,即栈的链式存储结构,链栈是一种数据存储结构,可以通过单链表的方式来实现,使用链式栈的优点在于它能够克服用数组实现的顺序栈空间利用率不高的特点,但是需要为每个栈元素分配额外的指针空间用来存放指针域。
这里我们需要思考,我们应该如何用单链表来实现栈这一种存储方式呢?如图为不带头节点的单链表:
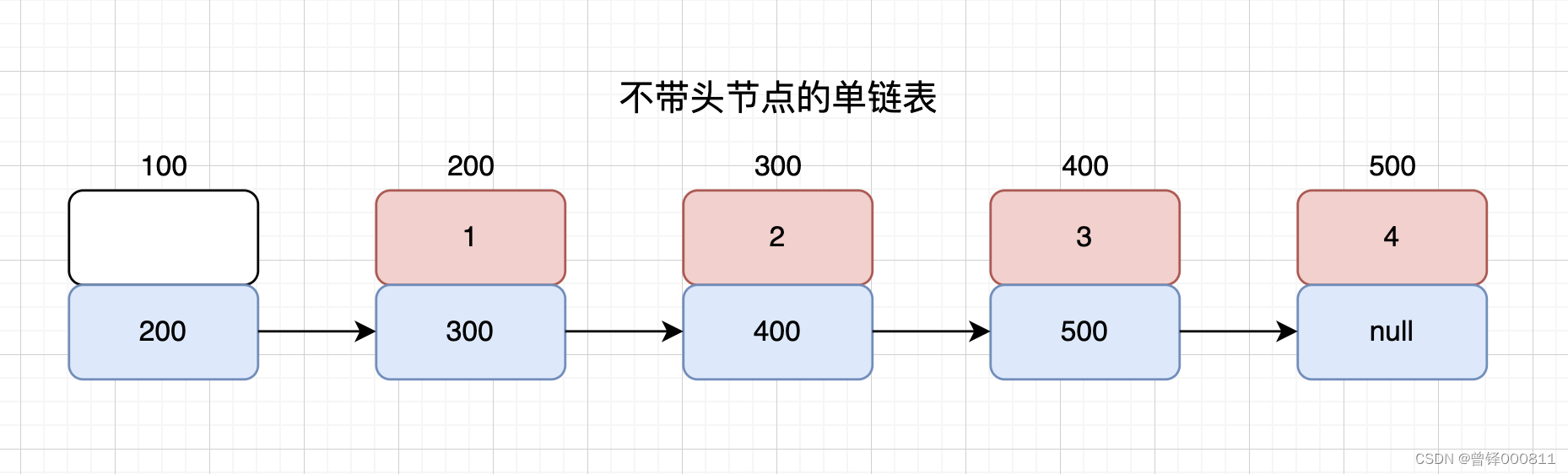
在之前我们讲过,栈(Stack)这种东西,就是限定仅在表尾进行插入或删除操作的线性表。
所以我们依照栈的特性,我们就将这个吞吐的口设定在单链表的头节点和第一个有效节点之间,其实也就是我们之前实现过的单链表中的头插和头删功能。
这玩意儿也没啥难的,说白了,就是阉割版的单链表。
代码实现:
链栈中要实现的功能函数:
初始化函数(Init_Stack);
清空函数(Clear);
销毁函数(Destroy);
打印函数(Show);
查找函数(Search);
入栈函数(Push);
出栈函数(Pop);
返回栈顶元素函数(Top);
判空函数(IsEmpty);
获取有效数据个数函数(Get_Length);
头文件(Chain_Stack.h):
设置链栈中的元素范型:
typedef int Elem_type;链栈的结构体设计:
typedef struct CStack
{
Elem_type data;
struct CStack* next;
}Stack,*PStack;所有功能函数的声明:
void Init_Stack(PStack cstack);
void Clear(PStack cstack);
void Destroy(PStack cstack);
void Show(PStack cstack);
PStack Search(PStack cstack,Elem_type val);
bool Push(PStack cstack,Elem_type val);
bool Pop(PStack cstack);
Elem_type top(PStack cstack);
bool IsEmpty(PStack cstack);
int Get_Length(PStack cstack);源文件(Chain_Stack.cpp)对函数功能的具体实现:
初始化函数(Init_Stack):
void Init_Stack(PStack cstack)
{
assert(cstack != nullptr);
cstack->next = nullptr;
}清空函数(Clear);
void Clear(PStack cstack)
{
Destroy(cstack);
}销毁函数(Destroy):
void Destroy(PStack cstack)
{
assert(cstack != nullptr);
while (!IsEmpty(cstack)){
Pop(cstack);
}
}打印函数(Show):
void Show(PStack cstack)
{
assert(cstack != nullptr);
PStack p = cstack->next;
for(;p != nullptr;p = p->next){
printf("%3d", p->data);
}
}查找函数(Search):
PStack Search(PStack cstack,Elem_type val)
{
assert(cstack != nullptr);
PStack p = cstack->next;
assert(p != nullptr);
for(;p != nullptr;p = p->next){
if(val == p->data){
return p;
}
}
return nullptr;
}入栈函数(Push):
bool Push(PStack cstack,Elem_type val)
{
assert(cstack != nullptr);
PStack pnewnode = (PStack)malloc(1 * sizeof(Stack));
assert(pnewnode != nullptr);
pnewnode->data = val;
pnewnode->next = cstack->next;
cstack->next = pnewnode;
return true;
}出栈函数(Pop):
bool Pop(PStack cstack)
{
assert(cstack != nullptr);
if(IsEmpty(cstack)){
return false;
}
PStack p = cstack->next;
assert(p != nullptr);
cstack->next = p->next;
return true;
}返回栈顶元素函数(Top):
Elem_type top(PStack cstack)
{
assert(cstack != nullptr);
PStack p = cstack->next;
for(;p != nullptr;p = p->next);
printf("%3d",p->data);
}判空函数(IsEmpty):
bool IsEmpty(PStack cstack)
{
assert(cstack != nullptr);
return cstack->next == nullptr;
}获取有效数据个数函数(Get_Length):
int Get_Length(PStack cstack)
{
assert(cstack != nullptr);
int count = 0;
PStack p = cstack->next;
for(;p != nullptr;p = p->next){
count++;
}
return count;
}
测试:
测试初始化函数、打印函数:
#include "Chain_Stack.h"
#include<cstdio>
int main()
{
Stack chain;
Init_Stack(&chain);
for(int i = 0;i < 10;i++){
Push(&chain,i + 1);
}
printf("原始数据为:\n");
Show(&chain);
return 0;
/*
此处添加其他测试代码...
*/
}运行结果:

测试清空函数:
Clear(&chain);
printf("\n经过清空操作之后的数据为:\n");
Show(&chain);运行结果:
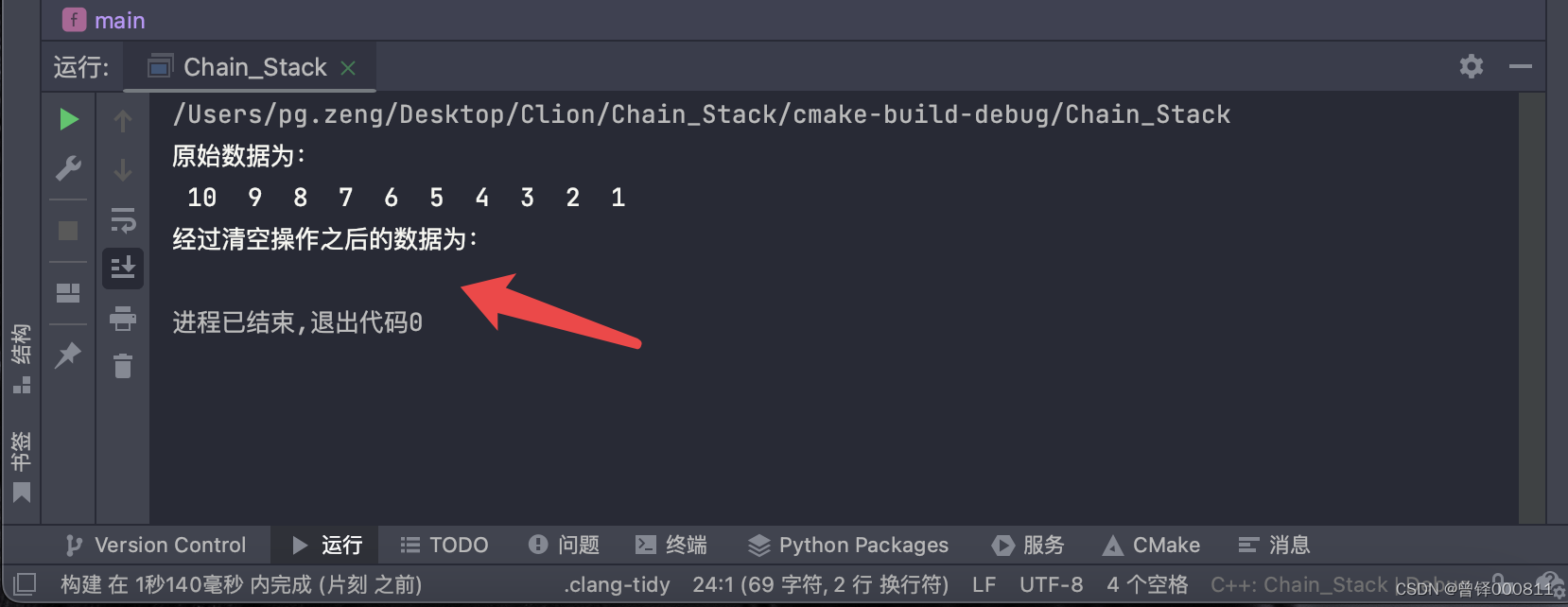
测试销毁函数:
Destroy(&chain);
printf("\n经过销毁操作之后的数据为:\n");
Show(&chain);运行结果:
 测试查找函数:
测试查找函数:
PStack p = Search(&chain,2);
printf("\n元素2在链栈中的地址为:%p\n",p);运行结果:
 测试入栈函数:
测试入栈函数:
Push(&chain,11);
printf("\n经过入栈操作之后的数据为:\n");
Show(&chain);运行结果:
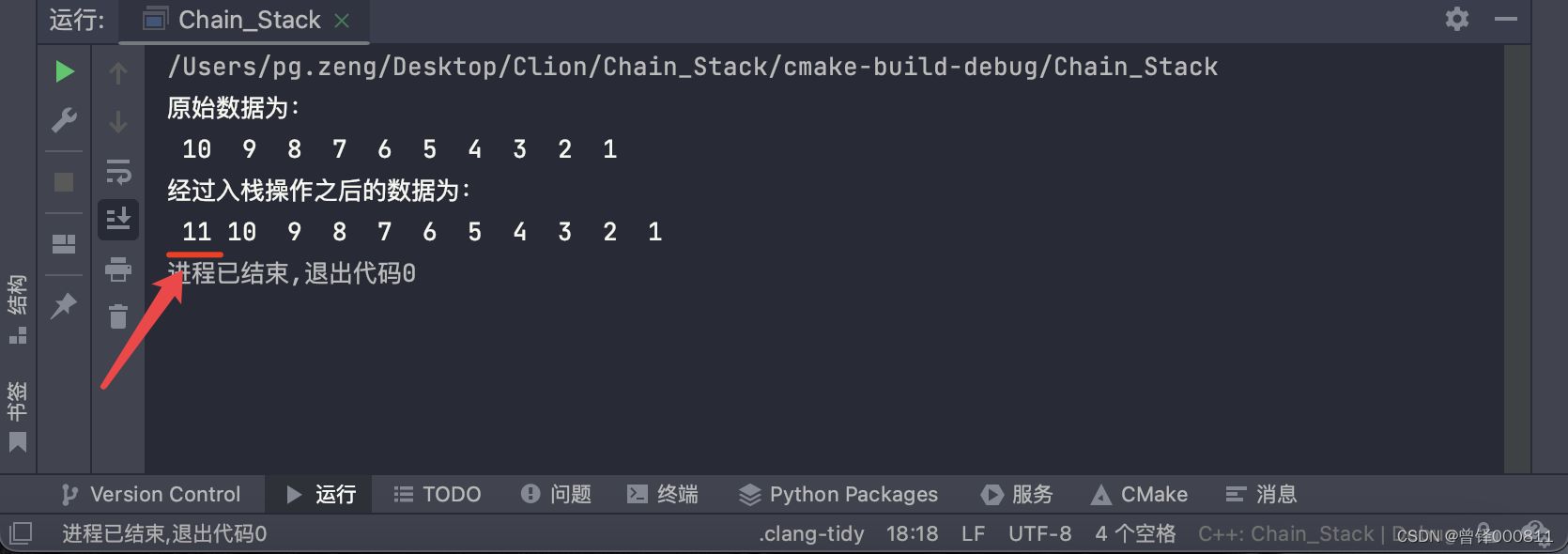
测试出栈函数:
Pop(&chain);
printf("\n经过一个出栈后的数据为:\n");
Show(&chain);运行结果:

测试返回栈顶元素函数:
printf("\n栈顶元素为:%3d",top(&chain));运行结果:
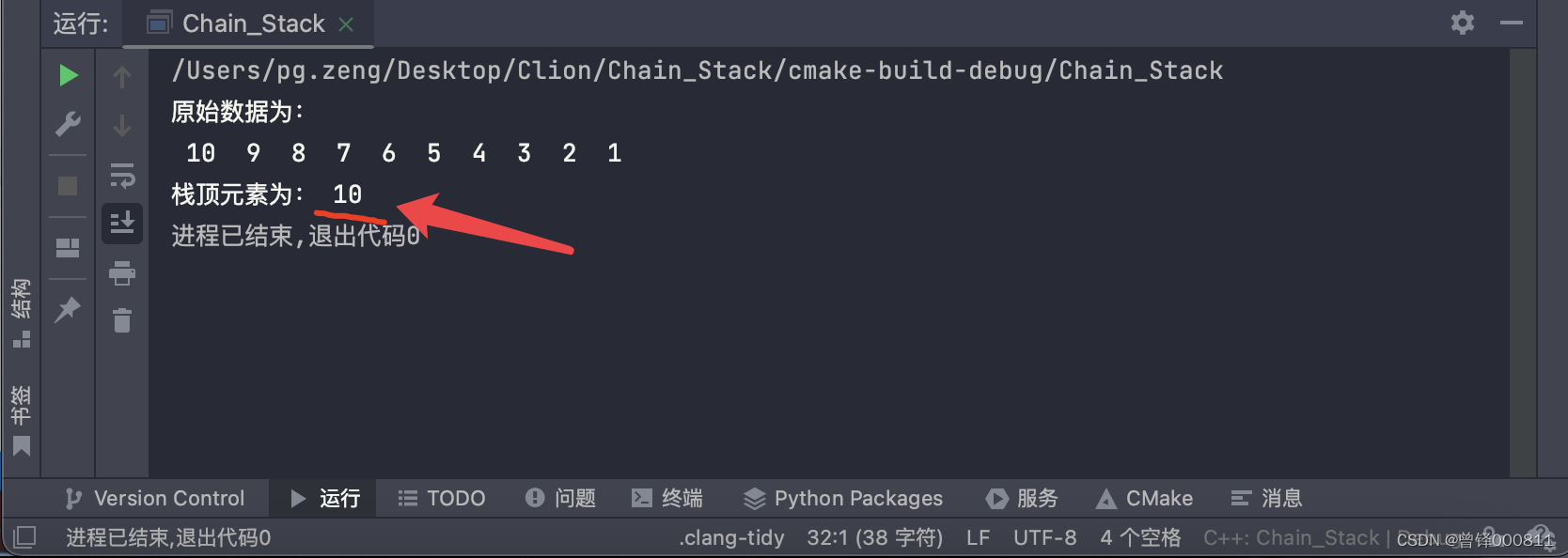

![[附源码]java毕业设计代驾服务系统](https://img-blog.csdnimg.cn/44e472bf9d3e40c9af315cc2991b0afe.png)