一、线性表的定义

线性表是 n (n >= 0) 个具有相同特性的数据元素的有限序列。线性表是一种在实际中广泛使用的数据结构，常见的线性表:顺序表、链表、栈、队列…
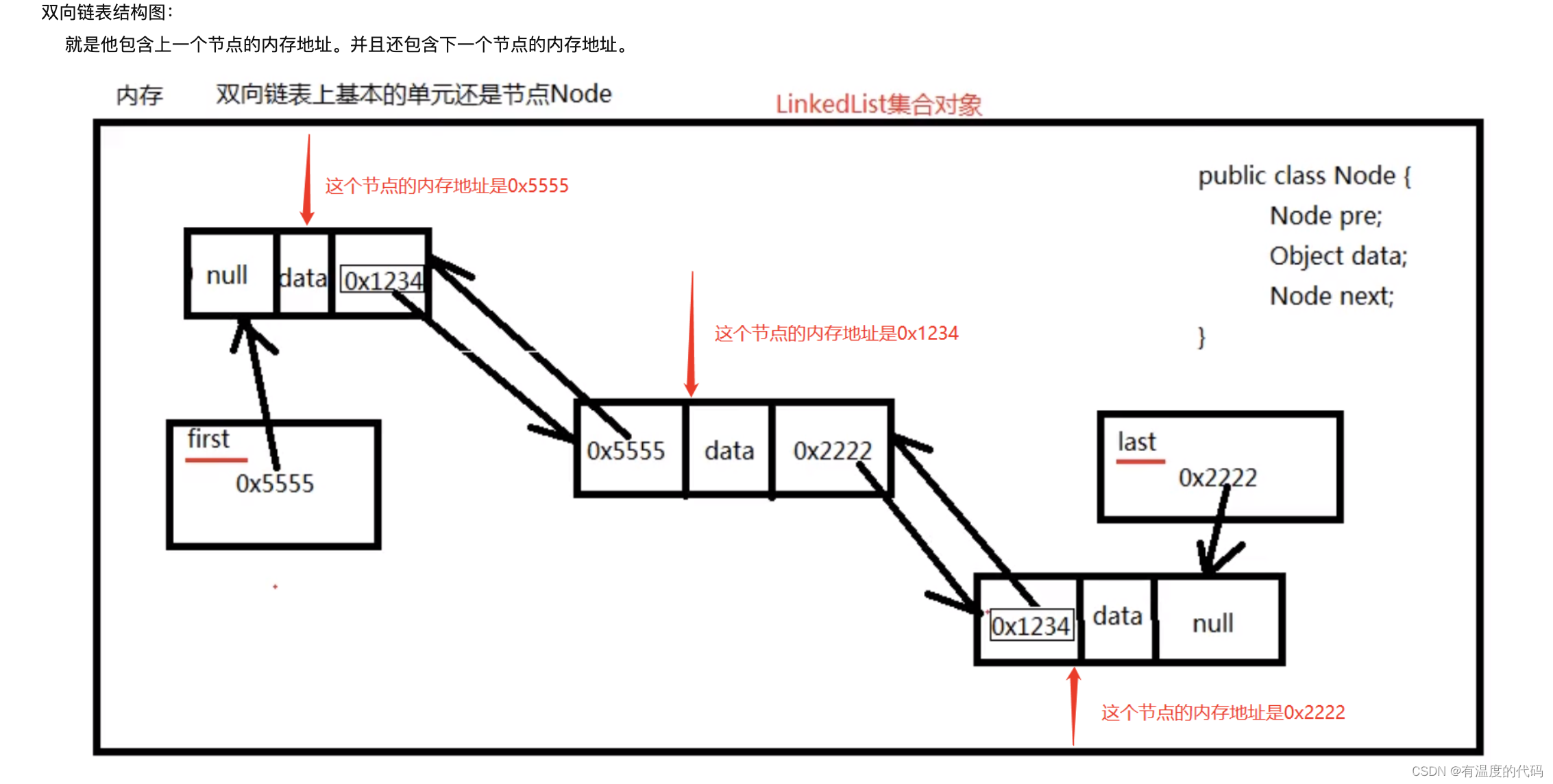
线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的线性表在物理上存储时，通常以数组和链式结构的形式存储。

数组形式

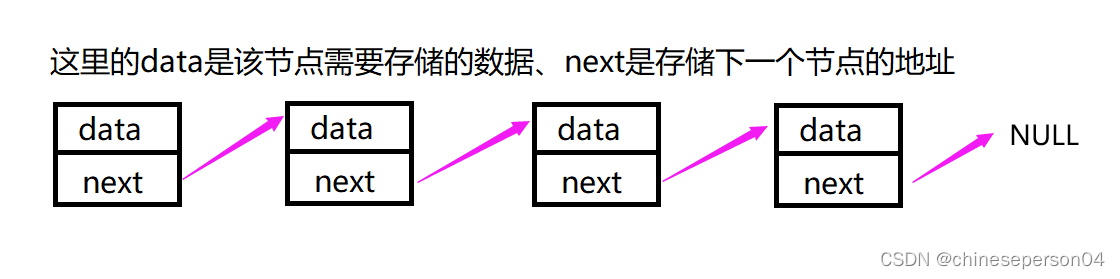
在这里插入图片描述

链表形式

在这里插入图片描述

二、顺序表

1. 顺序表的定义

顺序表是一种线性数据结构，通过连续的内存空间存储元素，可以随机访问任何位置的元素。它支持在常量时间内进行插入、删除和访问操作，但在插入或删除元素时可能需要移动后续元素，导致时间复杂度为O(n)。

2. 顺序表的结构

2.1 静态顺序表

静态顺序表使用定长数组，当数组存储满后则不能再进行存储。
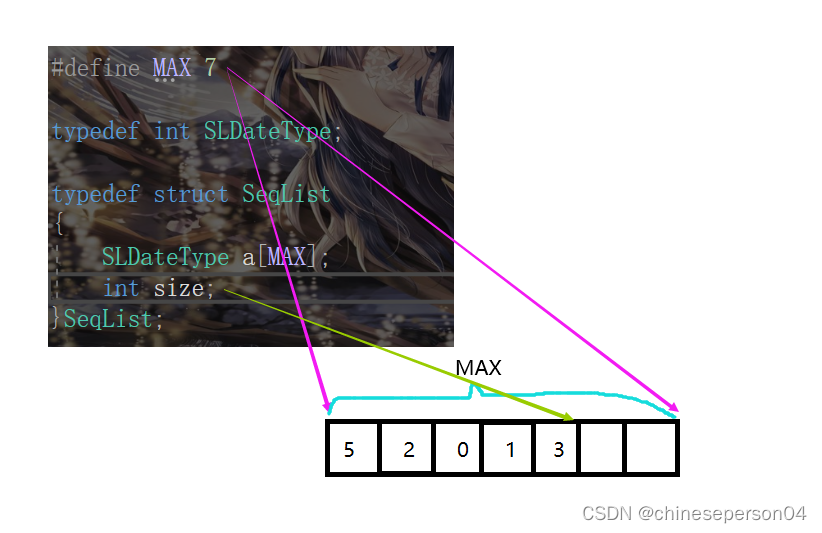
在这里插入图片描述

2.2 动态顺序表

动态顺序表使用动态申请的数组进行存储，当顺序表被存满后，会自动扩大容量。

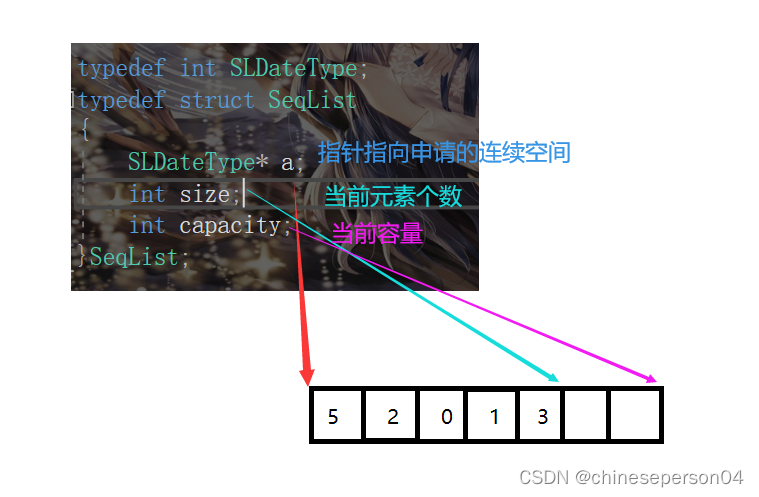
在这里插入图片描述

3. 动态顺序表的接口实现

3.1 顺序表的接口

typedef int SLDateType;
typedef struct SeqList
{
	SLDateType* a;
	int size;
	int capacity;
}SeqList;

// 对数据的管理:增删查改 

//顺序表的初始化
void SeqListInit(SeqList* ps);
//顺序表的销毁
void SeqListDestroy(SeqList* ps);

//顺序表的打印
void SeqListPrint(SeqList* ps);
//顺序表的尾插
void SeqListPushBack(SeqList* ps, SLDateType x);
//顺序表的头插
void SeqListPushFront(SeqList* ps, SLDateType x);
//顺序表的的头删
void SeqListPopFront(SeqList* ps);
//顺序表的尾删
void SeqListPopBack(SeqList* ps);

// 顺序表查找
int SeqListFind(SeqList* ps, SLDateType x);
// 顺序表在pos位置插入x
void SeqListInsert(SeqList* ps, int pos, SLDateType x);
// 顺序表删除pos位置的值
void SeqListErase(SeqList* ps, int pos);

3.2 接口的实现

void SeqListInit(SeqList* ps)
{
	//动态申请十个 SLDateType 类型大小的空间
	ps->a = (SLDateType*)malloc(sizeof(SLDateType) * 10);
	//判断是否开辟成功
	if (ps->a == NULL)
	{
		perror("malloc");
		return;
	}  
	ps->size = 0;        //顺序表初始化，顺序表内无数据，则赋值为 0
	ps->capacity = 10;   //容量为动态申请的元素个数
}


void SeqListDestroy(SeqList* ps)
{
	//将动态申请的空间释放
	free(ps->a);
	ps->a = NULL;
}

int CheckSeqList(SeqList* ps)
{
	//检查顺序表是否被填满
	if (ps->capacity == ps->size)
	{
		//若填满则将动态申请的内存扩大为原来的两倍
		SLDateType* tmp = (SLDateType*)realloc(ps->a, sizeof(SLDateType) * (ps->capacity * 2));
		//定义一个变量接收扩大后返回空间的首地址
		//目的：若开辟失败也不会改变原来的内存
		if (tmp == NULL)
		{
			perror("realloc");
			return 0;
		}
		ps->a = tmp;
		//将容量变成原来的两倍
		ps->capacity *= 2;
	}
	return 1;
}


void SeqListPushBack(SeqList* ps, SLDateType x)
{
	//判断顺序表是否为满，未满则进行下面的步骤
	//若满了，则先扩容，再进行下面的步骤
	if (CheckSeqList(ps) == 0)
	{
		return;
	}
	
	//将需要尾插的数据放在下标为size的数组中
	ps->a[ps->size] = x;
	//存储的元素加一
	ps->size++;
}

void SeqListPrint(SeqList* ps)
{
	int i = 0;
	for (i = 0; i < ps->size; i++)
	{
		printf("%d ", ps->a[i]);
	}
}

void SeqListPushFront(SeqList* ps, SLDateType x)
{
	//判断顺序表是否为满，未满则进行下面的步骤
	//若满了，则先扩容，再进行下面的步骤
	if (CheckSeqList(ps) == 0)
	{
		return;
	}

	//下面省略的代码是没有用随机插入函数实现的
	/*int i = 0;
	for (i = ps->size - 1; i >= 0; i--)
	{
		//将所有的元素向后移动一位
		ps->a[i + 1] = ps->a[i];
	}
	ps->a[0] = x;   //将需要插入的元素放在首元素的位置
	ps->size++;*/	//存储元素个数加一
	
	//下面省略的代码是没有用随机插入函数实现的，并使用memmove函数移动数组
	
	/*memmove(ps->a + 1, ps->a, sizeof(SLDateType) * ps->size);
	ps->a[0] = x;
	ps->size++;*/
	
	//该代码是使用随机插入函数实现的
	SeqListInsert(ps, 0, x);
	
}


void SeqListPopFront(SeqList* ps)
{
	//下面省略的代码是没有用随机删除函数实现的
	//断言：顺序表为空不能删除
	//assert(ps->size != 0);
	/*int i = 0;
	//将首元素后面的元素全部向前移动一位
	for (i = 0; i < ps->size - 1; i++)
	{
		ps->a[i] = ps->a[i + 1];
	}
	ps->size--;*/  //存储元素个数减一

	//下面省略的代码是没有用随机删除函数实现的，并使用memmove函数移动数组
	/*memmove(ps->a, ps->a + 1, sizeof(SLDateType) * (ps->size - 1));
	ps->size--;*/ 
	
	//该代码是使用随机删除函数实现的
	SeqListErase(ps, 0);
}

void SeqListPopBack(SeqList* ps)
{
	//下面省略的代码是没有用随机删除函数实现的
	
	//断言：顺序表为空不能删除
	/*assert(ps->size != 0);
	ps->size--;*/ //存储元素个数减一
	
	//该代码是使用随机删除函数实现的
	SeqListErase(ps , ps ->size - 1);
}


int SeqListFind(SeqList* ps, SLDateType x)
{
	int i = 0;
	for (i = 0; i < ps->size; i++)
	{
		if (ps->a[i] == x)
		{
			return i;
		}
	}
	return -1;
}


void SeqListInsert(SeqList* ps, int pos, SLDateType x)
{
	int i = 0;
	//需要插入的位置不能在size下标元素的后面
	//原因是size - 1 下标中的元素是最后一个元素
	assert(ps->size >= pos);
	/*for (i = ps->size - 1; i >= pos; i--)
	{
		ps->a[i + 1] = ps->a[i];
	}
	ps->a[pos] = x;
	ps->size++;*/

	memmove(ps->a + pos + 1, ps->a + pos, sizeof(SLDateType)*(ps->size - pos));
	ps->a[pos] = x;
	ps->size++;
}

void SeqListErase(SeqList* ps, int pos)
{
	//顺序表不能为空
	assert(ps->size != 0);
	int i = 0;
	//将需要删除元素的后面的元素全部向前移动一位
	for (i = pos; i < ps->size - 1; i++)
	{
		ps->a[i] = ps->a[i + 1];
	}
	ps->size--;
}