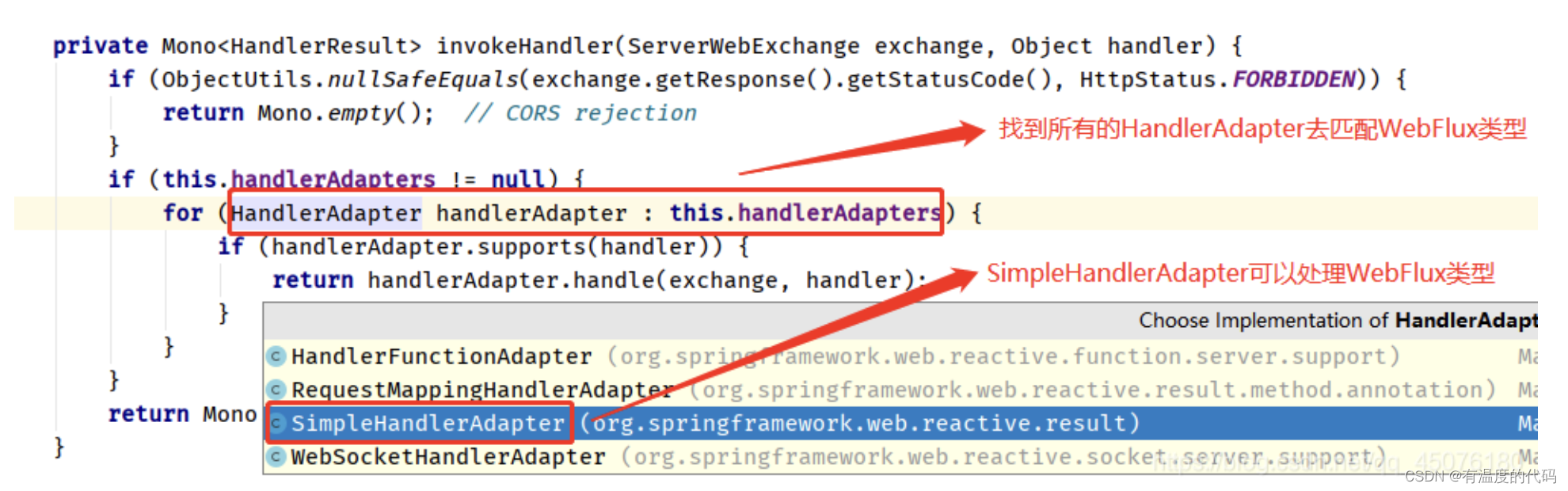
一、一阶速度-应力弹性波方程

在二维各向同介质xoz平面内，假定体力为0。
从上面方程当中，我们为了得到各点的应力和速度值，就需要得到关于对时间t和空间x，z的偏导。

二、时间上的2M阶差分

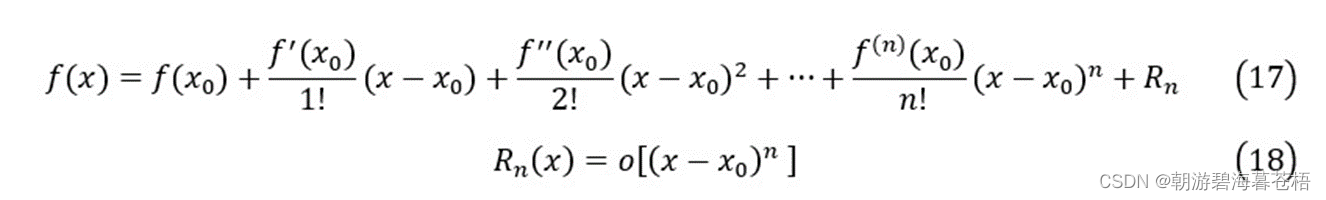
由Taylor公式得

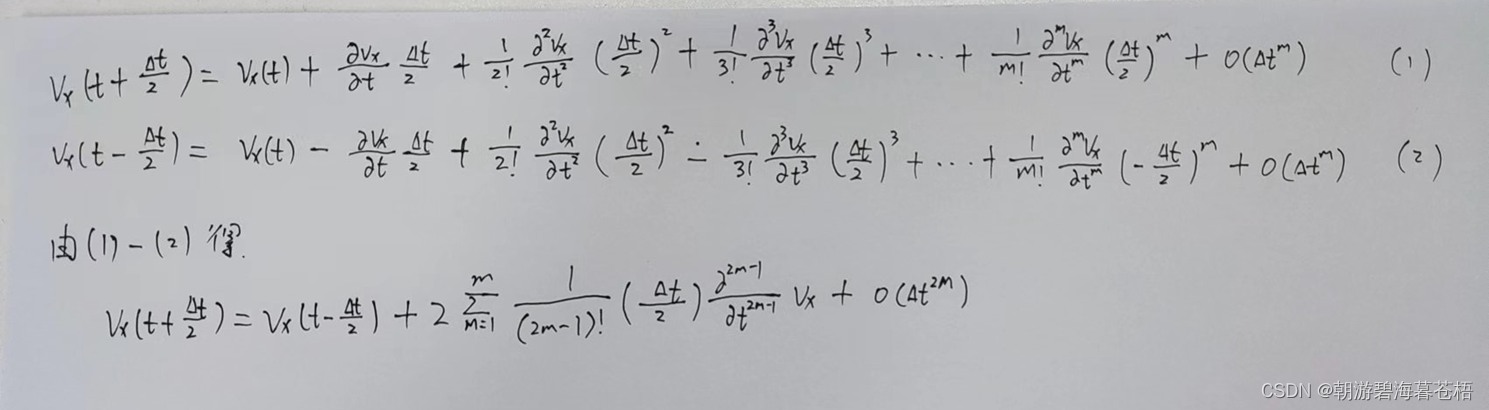
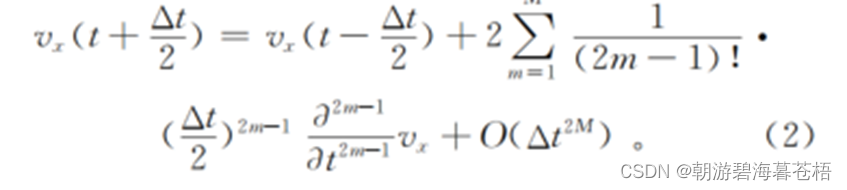
三、空间2N阶近似差分

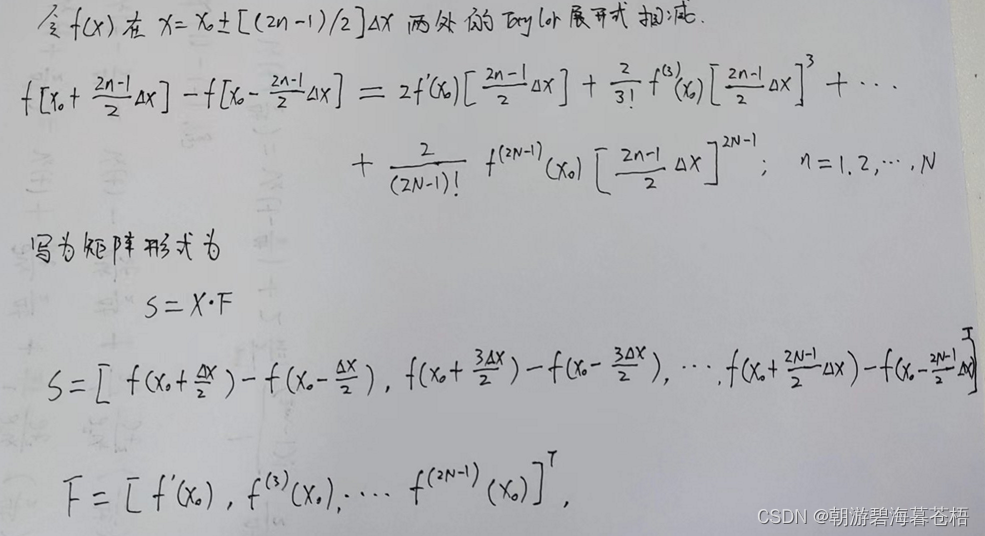
由一阶应力-速度弹性波方程，我们知道我们需要计算得到关于对x，z的偏导；即求出上式中的F;

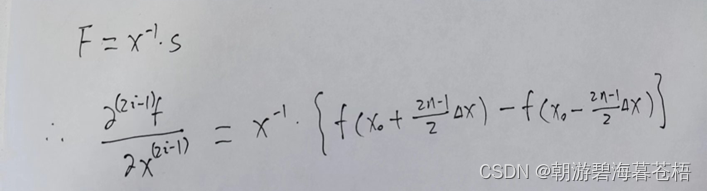
这里只剩下对于X的逆矩阵的求解了。

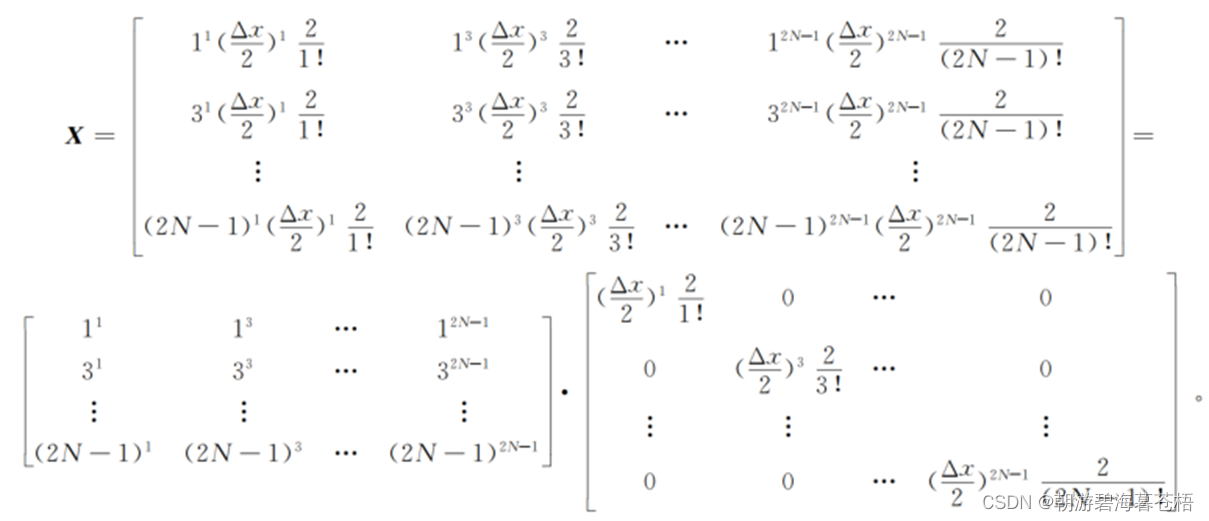
将X分解为

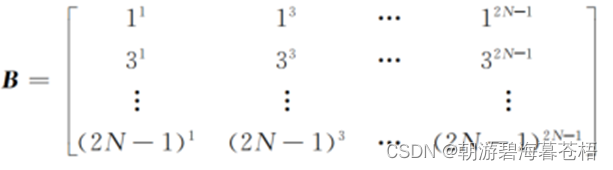
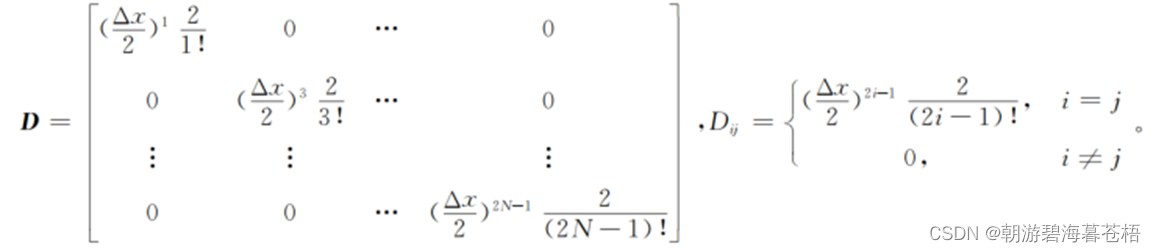
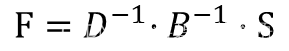
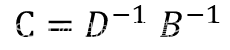
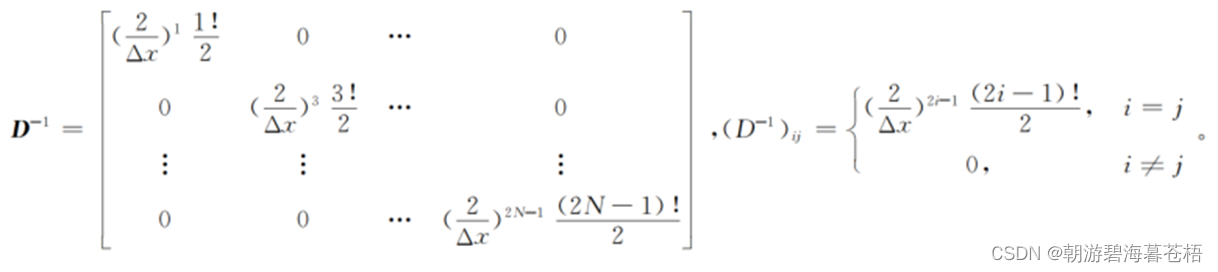
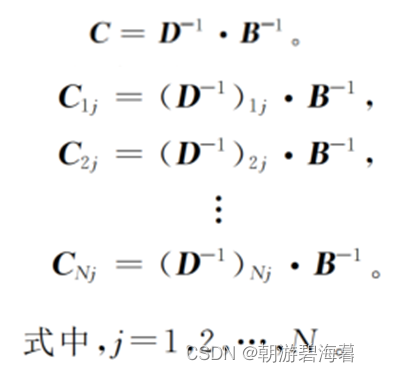
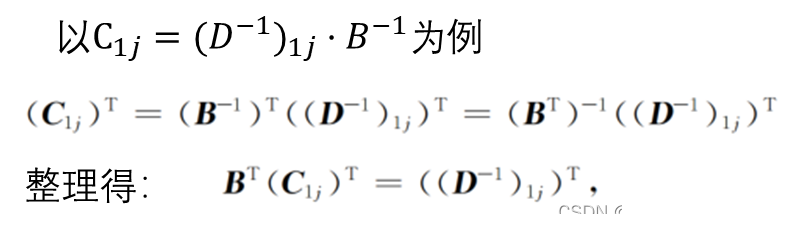
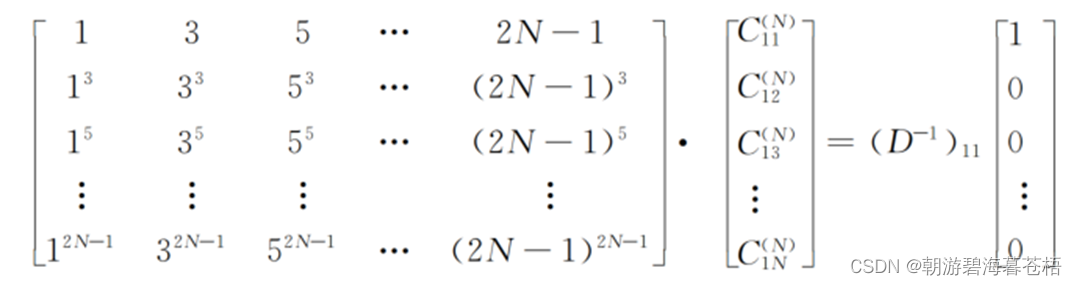
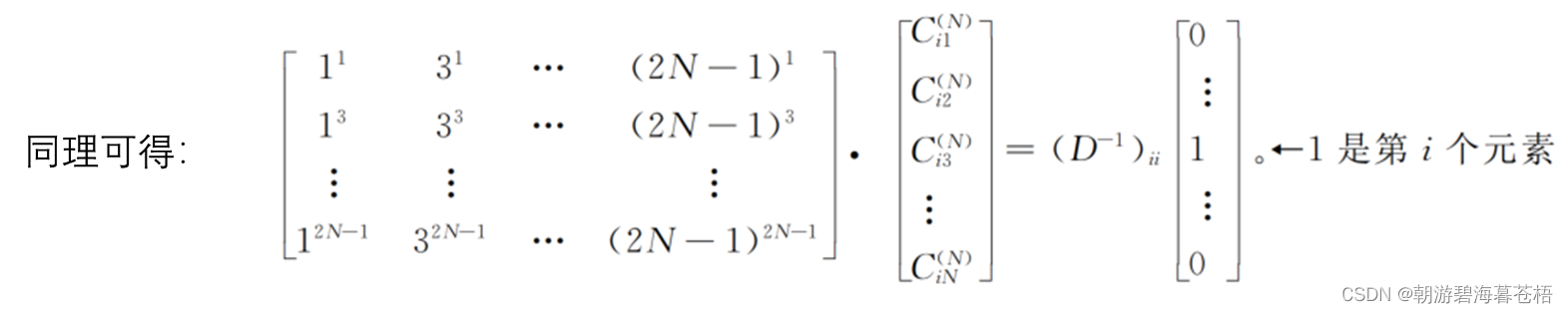
由上式中我们就可以计算出C的值；
查表可得C的值为

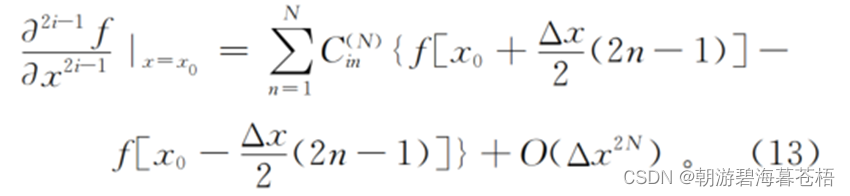
四、弹性波差分格式

各向同性介质一阶应力-速度方程组交错网格时间2阶，空间任意偶数阶差分格式：

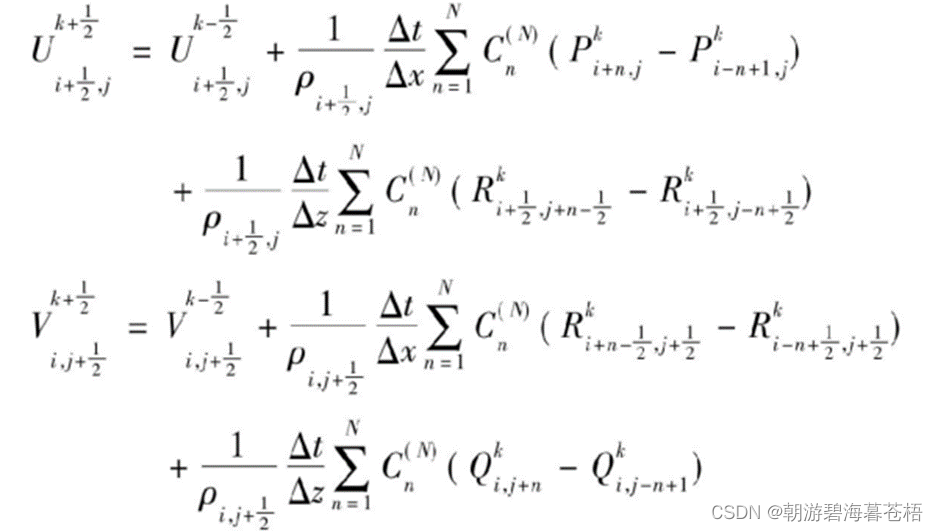
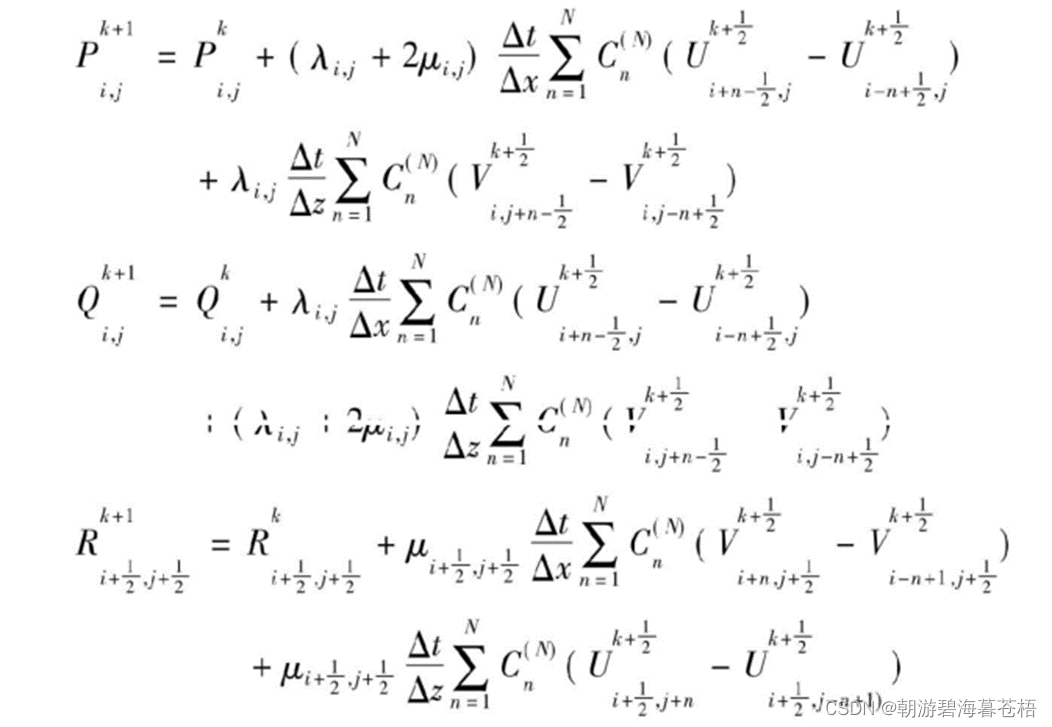
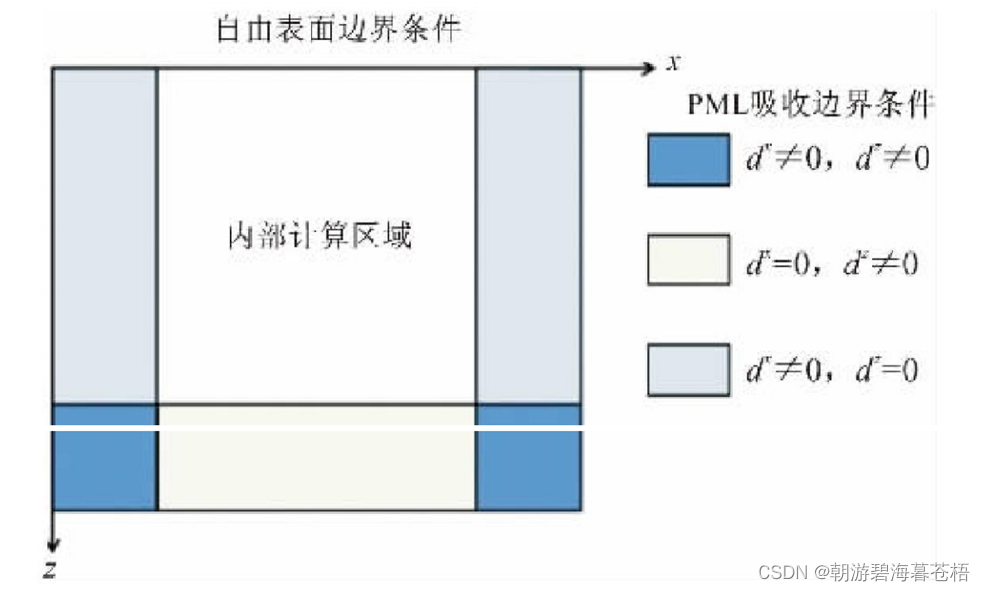
五、边界条件设置

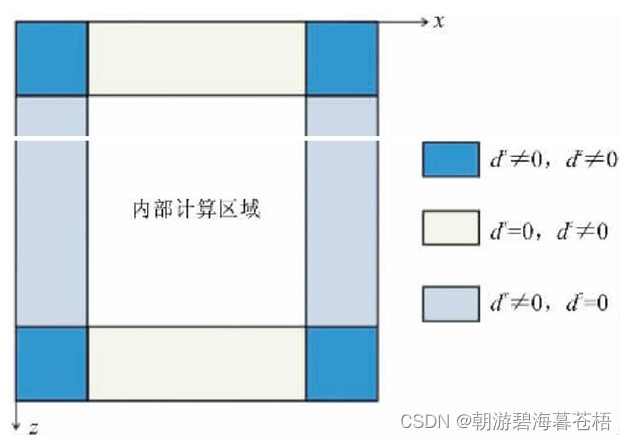
5.1 人工边界吸收条件

PML基本原理：在吸收层内给出一个方程去耦合计算区域的波动方程，使得在交界处没有反射，同时波在吸收层内呈指数衰减。



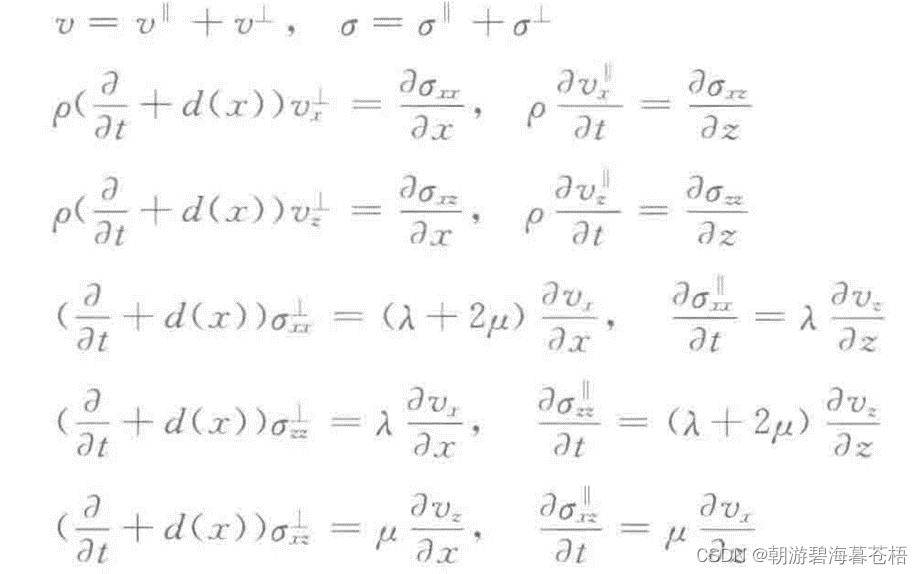
最终得到速度-应力差分公式

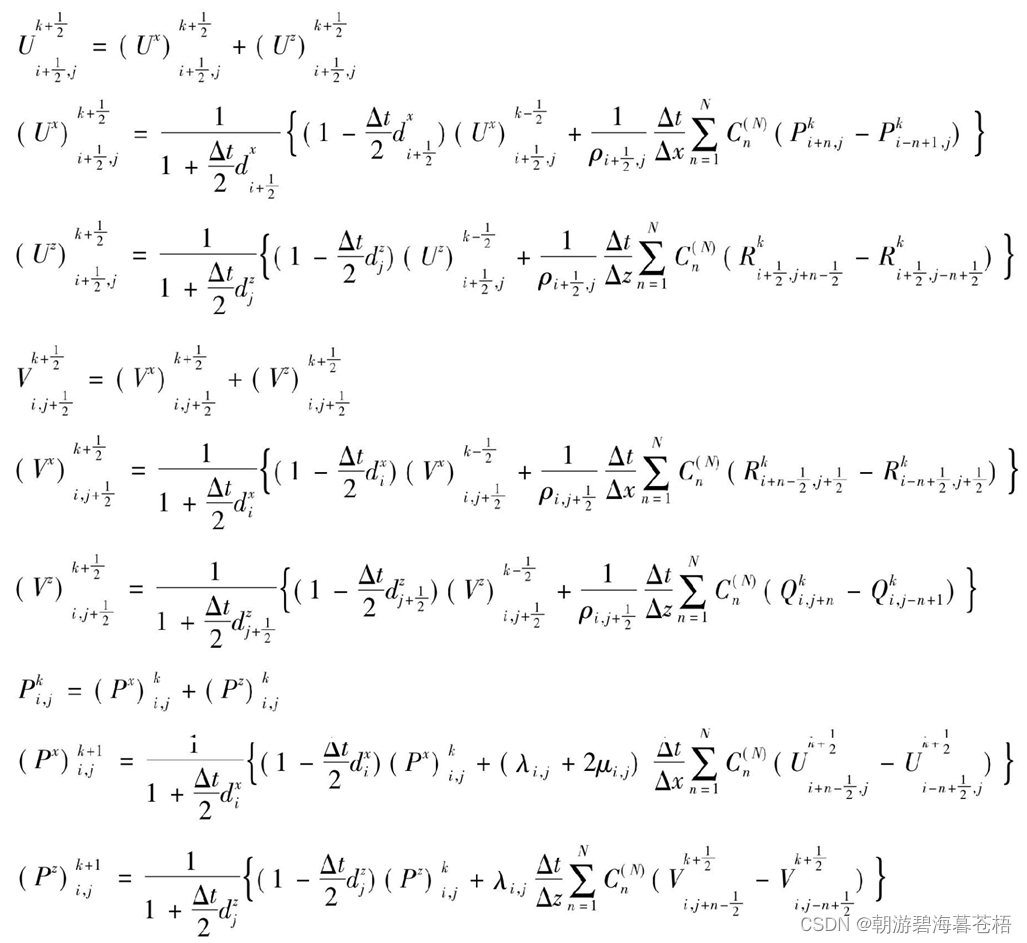
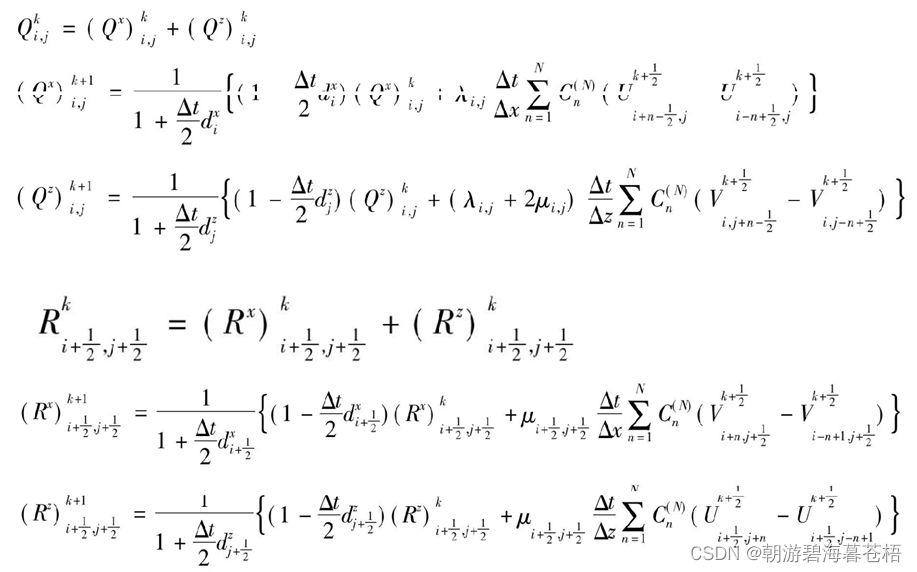
5.2 自由界面边界条件

声学和弹性介质边界近似代替自由界面（AEA方法）


参考文献：《高频面波法》夏江海老师
[1]杨庆节,刘财,耿美霞,冯晅,郭智奇,刘洋.交错网格任意阶导数有限差分格式及差分系数推导[J].吉林大学学报(地球科学版),2014,44(01):375-385.DOI:10.13278/j.cnki.jjuese.201401307.