2.1引言

综述

线性连续时间系统的时域分析，就是建立和求解线性微分方程的过程

n阶线性系统

1.数学模型

2.解法

古典解法

解法：系统全响应 = 自然响应（齐次方程通解）+ 受迫响应（非齐次方程特解）
缺点：对于复杂激励信号的求解困难

近代时域法（卷积法、算子法）

解法： 系统全响应 = 零输入响应 （古典解法求解）+ 零状态响应（叠加积分法或变换域法）

叠加积分法

1.本质

利用线性系统的齐次性和叠加性，将各个子信号的响应叠加得到整个系统的零状态响应

2. 待解决问题

选用何种子信号作为任意复杂信号的基础
如何分解复杂信号
如何求子信号响应
如何将子信号响应叠加

2.2系统方程的算子表示法

算子及其运算规则

1.微分算子和积分算子

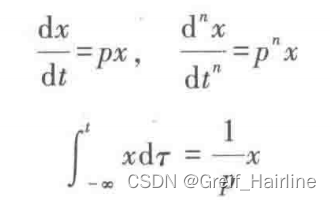
2.运算规则

  代数运算规则一般适用，只是在分子分母中或在等式两边相同的算子符号不能随便消去

3.电容和电感的伏安特性

转移算子

1.定义

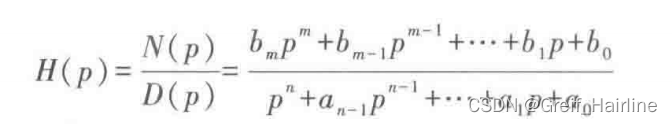
2.用转移算子表示响应与激励之间的关系