1. Anomaly detection
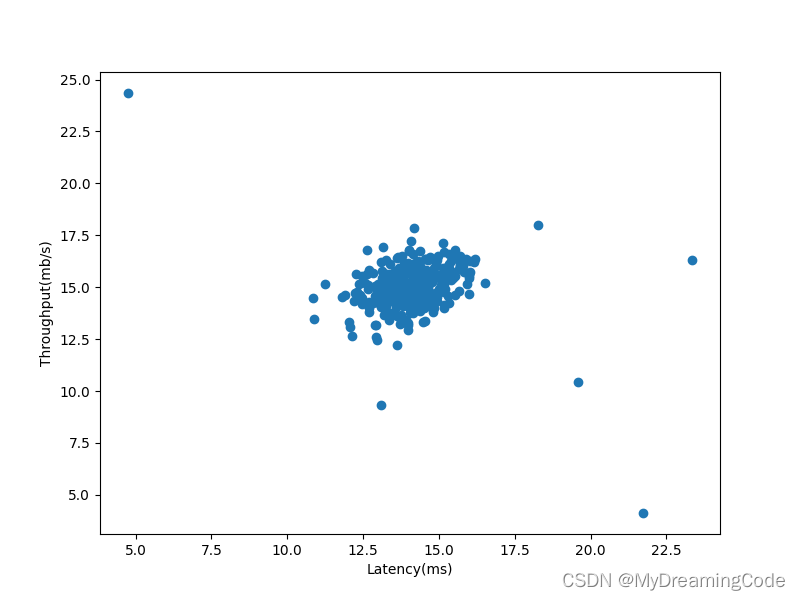
内容:使用高斯模型来检测数据集中异常的数据(概率低的),先在2维数据中进行实验。样本具有两个特征:a. 服务器响应的吞吐量(mb/s) b. 延迟(ms)。
数据可视化
main.py
from scipy.io import loadmat
import matplotlib.pyplot as plt
X = loadmat('ex8data1.mat')['X']
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(X[:, 0], X[:, 1])
ax.set_xlabel('Latency(ms)')
ax.set_ylabel('Throughput(mb/s)')
plt.show()
1.1 Gaussian distribution
内容:对每个特征 都拟合一个高斯分布。
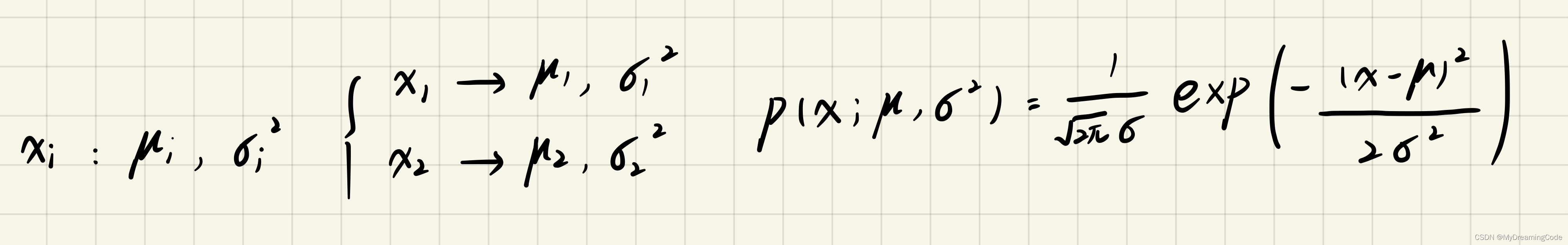
1.2 Estimating parameters for a Gaussian
内容:计算高斯分布函数的参数。输入一个X矩阵,得出一个包含n个特征的平均值mean和包含n个特征的sigma2。

estimateGaussian.py
def estimateGaussian(X):
mean = X.mean(axis=0)
sigma2 = X.var(axis=0)
return mean, sigma2
main.py
from scipy.io import loadmat
from estimateGaussian import * # 估算高斯分布的参数
X = loadmat('ex8data1.mat')['X']
mean, sigma2 = estimateGaussian(X)
print(mean, sigma2)
[14.11222578 14.99771051] [1.83263141 1.70974533]
数据可视化:
np.meshgrid为生成网络点坐标,如:
xplot = np.linspace(0, 25, 100)
yplot = np.linspace(0, 25, 100)
Xplot, Yplot = np.meshgrid(xplot, yplot) # 生成网格点坐标
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(Xplot, Yplot, s=5)
plt.show()
gaussianDistribution.py
import numpy as np
def gaussianDistribution(X, mean, sigma2):
sigma2 = np.reshape(sigma2, (1, 2))
mean = np.reshape(mean, (1, 2))
p = (1 / (np.sqrt(2 * np.pi) * sigma2)) * (np.exp(-(X - mean) ** 2 / (2 * sigma2)))
# prod为累乘
return np.prod(p, axis=1)
main.py
from scipy.io import loadmat
import numpy as np
import matplotlib.pyplot as plt
from estimateGaussian import * # 估算高斯分布的参数
from gaussianDistribution import * # 计算高斯分布函数
X = loadmat('ex8data1.mat')['X']
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(X[:, 0], X[:, 1])
mean, sigma2 = estimateGaussian(X)
gaussianDistribution(X, mean, sigma2)
xplot = np.linspace(0, 25, 100)
yplot = np.linspace(0, 25, 100)
Xplot, Yplot = np.meshgrid(xplot, yplot) # 生成网格点坐标
# 1.concatenate用于拼接数组
# 2.reshape(-1,1) 转换成1列
X = np.concatenate((Xplot.reshape(-1, 1), Yplot.reshape(-1, 1)), axis=1)
p = gaussianDistribution(X, mean, sigma2).reshape(Xplot.shape)
# 3.绘制等高线
# contour(X,Y,Z,[levels]) levels:确定轮廓线的数量和位置
contour = plt.contour(Xplot, Yplot, p, [10 ** -11, 10 ** -7, 10 ** -5, 10 ** -3, 0.1])
ax.set_xlabel('Latency(ms)')
ax.set_ylabel('Throughput(mb/s)')
plt.show()

1.3 Selecting the threshold, ε
内容:根据交叉验证集,使用 F1-score 来选择合适的阈值ε。低概率的数据可能是异常的。
精确率(precision)召回率(recall)
selectThreshold.py
import numpy as np
def selectThreshold(pval, yval):
best_epsilon = 0
best_f1 = 0
f1 = 0
step = (pval.max() - pval.min()) / 1000
# 1.np.arange(start,end,step):step为步长
# 2.np.logical_and(A,B) 返回A和B与逻辑后的布尔值
for epsilon in np.arange(pval.min(), pval.max(), step):
predicts = pval < epsilon # anomaly
# 虽然predicts(多一列)与yval列数不同,但是可以按照predicts的第一行与yval的第一行进行比较。
tp = np.sum(np.logical_and(predicts == 1, yval == 1)).astype(float)
fp = np.sum(np.logical_and(predicts == 1, yval == 0)).astype(float)
fn = np.sum(np.logical_and(predicts == 0, yval == 1)).astype(float)
prec = tp / (tp + fp) if tp + fp else 0
rec = tp / (tp + fn) if tp + fn else 0
f1 = (2 * prec * rec) / (prec + rec) if prec + rec else 0
if f1 > best_f1:
best_f1 = f1
best_epsilon = epsilon
return best_epsilon, best_f1
main.py
from scipy.io import loadmat
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
from estimateGaussian import * # 估算高斯分布的参数
from gaussianDistribution import * # 计算高斯分布
from selectThreshold import * # 选择阈值
raw_data = loadmat('ex8data1.mat')
X, Xval, yval = raw_data['X'], raw_data['Xval'], raw_data['yval']
mean, sigma2 = estimateGaussian(X)
# print(Xval.shape, yval.shape) (307, 2) (307, 1)
# 1.stats.norm(mean,sigma2).pdf:概率密度函数
p = np.zeros(X.shape)
p[:, 0] = stats.norm(mean[0], sigma2[0]).pdf(X[:, 0])
p[:, 1] = stats.norm(mean[1], sigma2[1]).pdf(X[:, 1])
# print(p.shape) # (307, 2)
# 2.验证集在相同模型参数下计算概率
pval = np.zeros(Xval.shape)
pval[:, 0] = stats.norm(mean[0], sigma2[0]).pdf(Xval[:, 0])
pval[:, 1] = stats.norm(mean[1], sigma2[1]).pdf(Xval[:, 1])
# print(pval.shape) # (307, 2)
epsilon, f1 = selectThreshold(pval, yval)
print(epsilon, f1)
0.009566706005956842 0.7142857142857143
可视化结果
main.py
from scipy.io import loadmat
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
from estimateGaussian import * # 估算高斯分布的参数
from gaussianDistribution import * # 计算高斯分布
from selectThreshold import * # 选择阈值
raw_data = loadmat('ex8data1.mat')
X, Xval, yval = raw_data['X'], raw_data['Xval'], raw_data['yval']
mean, sigma2 = estimateGaussian(X)
# print(Xval.shape, yval.shape) (307, 2) (307, 1)
# 1.stats.norm(mean,sigma2).pdf:概率密度函数
p = np.zeros(X.shape)
p[:, 0] = stats.norm(mean[0], sigma2[0]).pdf(X[:, 0])
p[:, 1] = stats.norm(mean[1], sigma2[1]).pdf(X[:, 1])
# print(p.shape) # (307, 2)
# 2.验证集在相同模型参数下计算概率
pval = np.zeros(Xval.shape)
pval[:, 0] = stats.norm(mean[0], sigma2[0]).pdf(Xval[:, 0])
pval[:, 1] = stats.norm(mean[1], sigma2[1]).pdf(Xval[:, 1])
# print(pval.shape) # (307, 2)
epsilon, f1 = selectThreshold(pval, yval)
# np.where(A)返回符合条件元素的坐标
outliers = np.where(p < epsilon)[0]
# print(outliers) # [300 301 301 303 303 304 306 306]
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(X[:, 0], X[:, 1])
ax.scatter(X[outliers, 0], X[outliers, 1], c='r', marker='o')
ax.set_xlabel('Latency(ms)')
ax.set_ylabel('Throughput(mb/s)')
plt.show()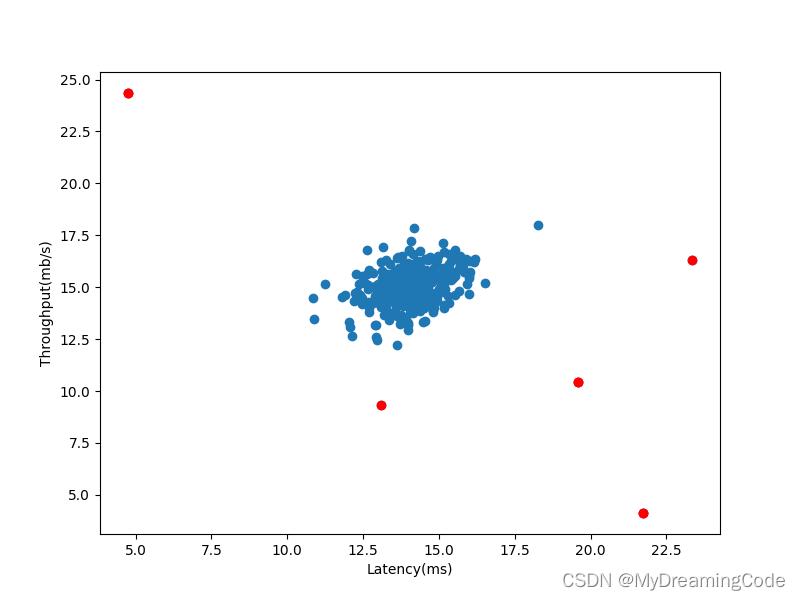
2. Recommender Systems
内容:该推荐系统将使用协同过滤算法在电影评级上进行应用。
2.1 Movie ratings dataset
内容:
n_movies:电影数量;n_users:用户数量
R(i,j):值为1表示用户 j 对电影 i 评分过,0表示未评分
y(i,j):评分(1-5),表示用户 j 对电影 i 的评分
矩阵:
X-电影的数据集(第 i 行表示由电影 i 组成的特征)
Theta-用户的数据集(第 j 行表示用户 j 对各类电影喜好程度的特征)
main.py
from scipy.io import loadmat
data = loadmat('ex8_movies.mat')
Y, R = data['Y'], data['R']
# print(Y.shape, R.shape) # (1682, 943) (1682, 943)
print(Y, R)
[[5 4 0 ... 5 0 0]
[3 0 0 ... 0 0 5]
[4 0 0 ... 0 0 0]
...
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]] [[1 1 0 ... 1 0 0]
[1 0 0 ... 0 0 1]
[1 0 0 ... 0 0 0]
...
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]]
评估电影的平均评级
main.py
from scipy.io import loadmat
import numpy as np
data = loadmat('ex8_movies.mat')
Y, R = data['Y'], data['R']
print(Y[1, np.where(R[1, :] == 1)].mean())
# 3.2061068702290076
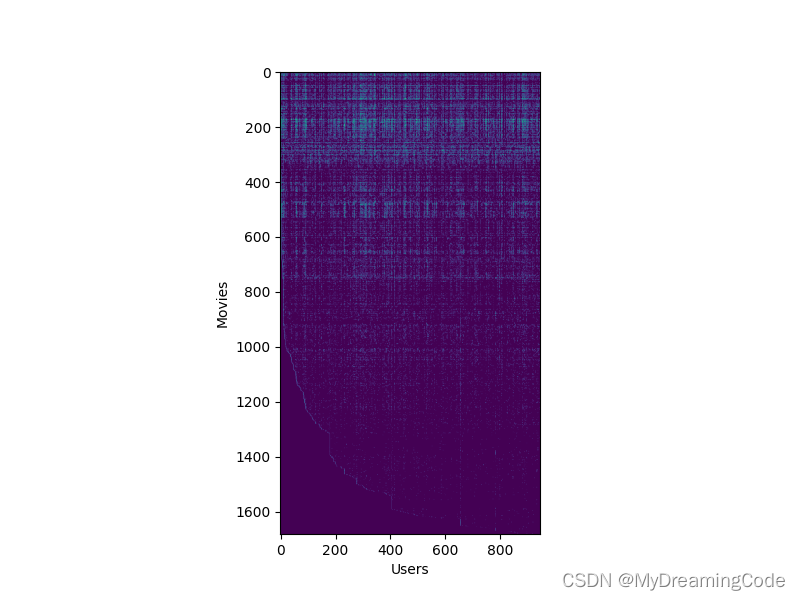
“可视化” 数据
main.py
from scipy.io import loadmat
import matplotlib.pyplot as plt
data = loadmat('ex8_movies.mat')
Y, R = data['Y'], data['R']
fig, ax = plt.subplots(figsize=(8, 6))
ax.imshow(Y)
ax.set_xlabel('Users')
ax.set_ylabel('Movies')
plt.show()
2.2 Collaborative filtering learning algorithm
内容:通过给定的一些用户评级电影的数据,并最小化代价函数,来学习参数X与Theta。
2.2.1 Collaborative filtering cost function
内容:

为了评估时间少一些,我们只取了少量的数据。(四位用户 五部电影 三个特征)
costFunction.py
import numpy as np
# 1.序列化
def serialize(X, theta):
return np.concatenate((X.ravel(), theta.ravel()))
# 2.逆序列化
def deserialize(param, n_movies, n_users, n_features):
return param[:n_movies * n_features].reshape(n_movies, n_features), param[n_movies * n_features:].reshape(n_users, n_features)
def costFunction(param, Y, R, n_features):
n_movies, n_users = Y.shape
X, theta = deserialize(param, n_movies, n_users, n_features)
return np.sum(np.power(np.multiply(X @ theta.T - Y, R), 2)) / 2
main.py
from scipy.io import loadmat
from costFunction import * # 代价函数
data = loadmat('ex8_movies.mat')
Y, R = data['Y'], data['R']
param_data = loadmat('ex8_movieParams.mat')
X, Theta = param_data['X'], param_data['Theta']
# 这里我们只取一小段数据
n_users = 4
n_movies = 5
n_features = 3
X_sub = X[:n_movies, :n_features]
Theta_sub = Theta[:n_users, :n_features]
Y_sub = Y[:n_movies, :n_users]
R_sub = R[:n_movies, :n_users]
param_sub = serialize(X_sub, Theta_sub)
print(costFunction(param_sub, Y_sub, R_sub, n_features))
param = serialize(X, Theta)
print(costFunction(param, Y, R, 10))
22.224603725685675
27918.64012454421
2.2.2 Collaborative filtering gradient
内容:计算梯度。
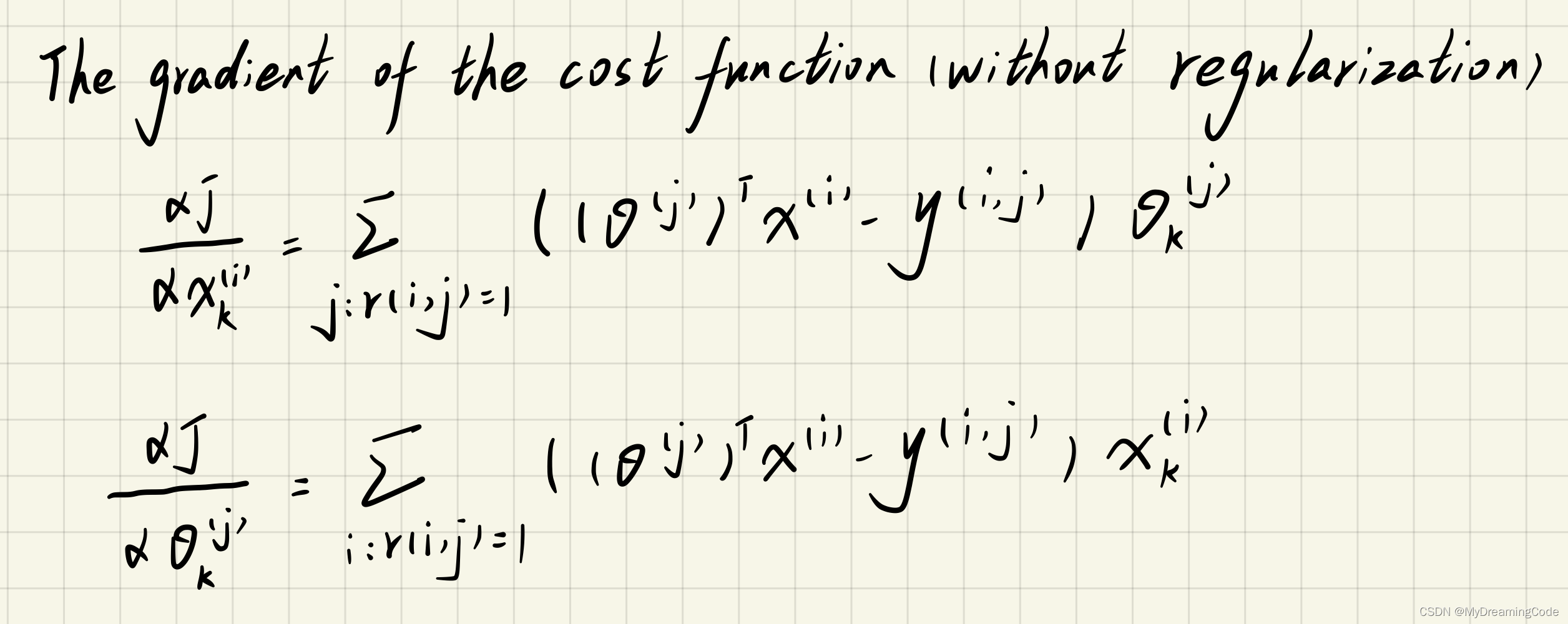
gradient.py
import numpy as np
from costFunction import * # 序列化与逆序列化的方法
def gradient(param, Y, R, n_features):
n_movies, n_users = Y.shape
X, Theta = deserialize(param, n_movies, n_users, n_features)
inner = np.multiply(X @ Theta.T - Y, R)
X_grad = inner @ Theta
Theta_grad = inner.T @ X
return serialize(X_grad, Theta_grad)
main.py
from scipy.io import loadmat
from gradient import * # 计算梯度
data = loadmat('ex8_movies.mat')
Y, R = data['Y'], data['R']
param_data = loadmat('ex8_movieParams.mat')
X, Theta = param_data['X'], param_data['Theta']
param = serialize(X, Theta)
n_movies, n_users = Y.shape
n_features = X.shape[1]
X_grad, Theta_grad = deserialize(gradient(param, Y, R, n_features), n_movies, n_users, n_features)
print(X_grad, Theta_grad)
[[-6.26184144 2.45936046 -6.87560329 ... -4.81611896 3.84341521
-1.88786696]
[-3.80931446 1.80494255 -2.63877955 ... -3.55580057 2.1709485
2.65129032]
[-3.13090116 2.54853961 0.23884578 ... -4.18778519 3.10538294
5.47323609]
...
[-1.04774171 0.99220776 -0.48920899 ... -0.75342146 0.32607323
-0.89053637]
[-0.7842118 0.76136861 -1.25614442 ... -1.05047808 1.63905435
-0.14891962]
[-0.38792295 1.06425941 -0.34347065 ... -2.04912884 1.37598855
0.19551671]] [[-1.54728877 9.0812347 -0.6421836 ... -3.92035321 5.66418748
1.16465605]
[-2.58829914 2.52342335 -1.52402705 ... -5.46793491 5.82479897
1.8849854 ]
[ 2.14588899 2.00889578 -4.32190712 ... -6.83365682 1.78952063
0.82886788]
...
[-4.59816821 3.63958389 -2.52909095 ... -3.50886008 2.99859566
0.64932177]
[-4.39652679 0.55036362 -1.98451805 ... -6.74723702 3.8538775
3.94901737]
[-3.75193726 1.44393885 -5.6925333 ... -6.56073746 5.20459188
2.65003952]]
2.2.3 Regularized cost function
内容:正则化代价函数

regularizedContent.py
import numpy as np
from costFunction import * # 引入未正则化的代价函数
def regularizedCostFunction(param, Y, R, n_features, learningRate):
reg = (learningRate / 2) * np.power(param, 2).sum()
return costFunction(param, Y, R, n_features) + reg
main.py
from scipy.io import loadmat
from gradient import * # 计算梯度
from regularizedContent import * # 带正则化的代价函数和梯度计算
data = loadmat('ex8_movies.mat')
Y, R = data['Y'], data['R']
param_data = loadmat('ex8_movieParams.mat')
X, Theta = param_data['X'], param_data['Theta']
n_users = 4
n_movies = 5
n_features = 3
X_sub = X[:n_movies, :n_features]
Theta_sub = Theta[:n_users, :n_features]
Y_sub = Y[:n_movies, :n_users]
R_sub = R[:n_movies, :n_users]
param_sub = serialize(X_sub, Theta_sub)
learningRate = 1.5
print(regularizedCostFunction(param_sub, Y_sub, R_sub, n_features, learningRate))
param = serialize(X, Theta)
print(regularizedCostFunction(param, Y, R, 10, learningRate=1))
31.34405624427422
32520.682450229557
2.2.4 Regularized gradient
内容:正则化梯度。
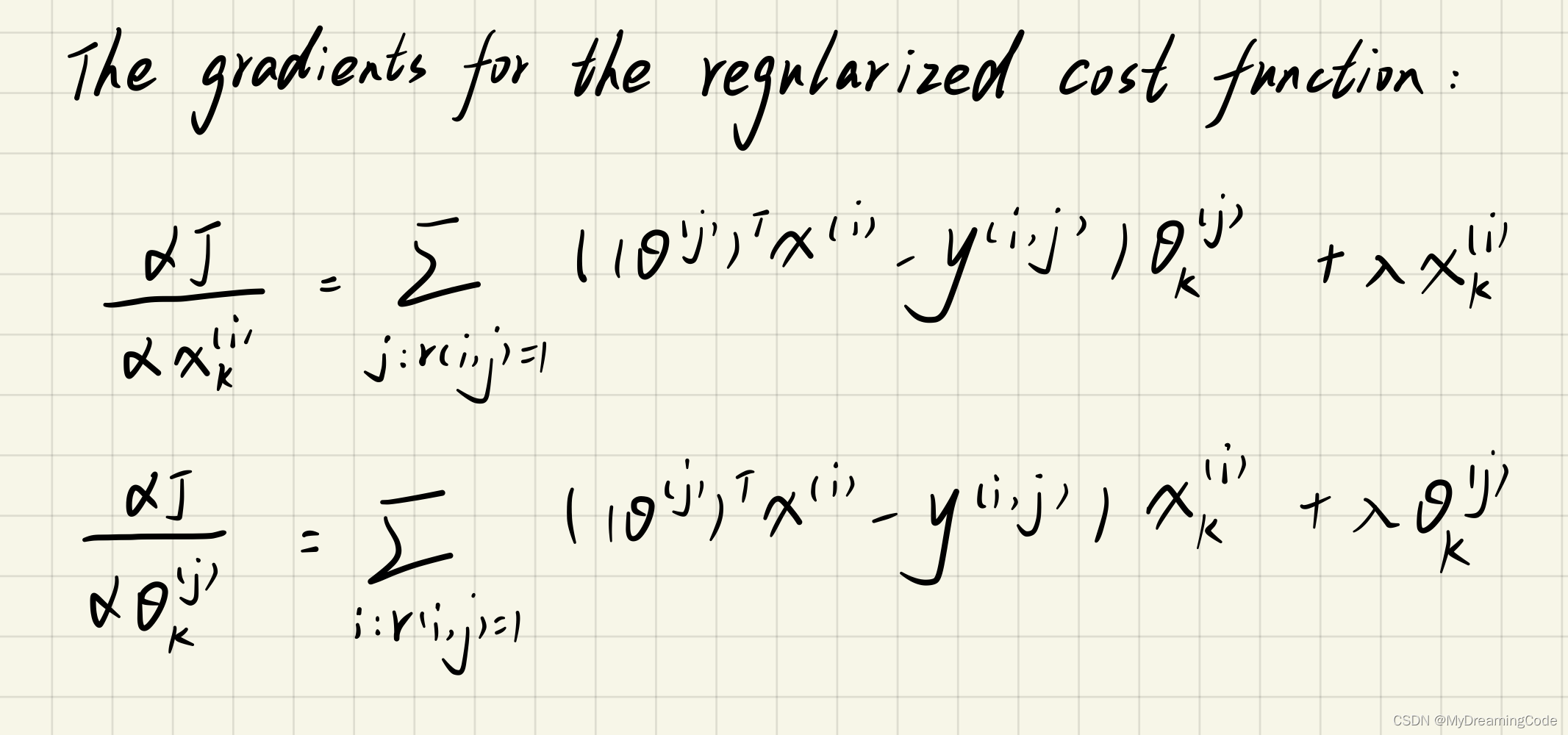
regularizedContent.py
import numpy as np
from costFunction import * # 引入未正则化的代价函数
from gradient import * # 引入未正则化的梯度计算
def regularizedCostFunction(param, Y, R, n_features, learningRate):
reg = (learningRate / 2) * np.power(param, 2).sum()
return costFunction(param, Y, R, n_features) + reg
def regularizedGradient(param, Y, R, n_features, learningRate):
grad = gradient(param, Y, R, n_features)
reg = learningRate * param
return grad + reg
main.py
from scipy.io import loadmat
from gradient import * # 计算梯度
from regularizedContent import * # 带正则化的代价函数和梯度计算
data = loadmat('ex8_movies.mat')
Y, R = data['Y'], data['R']
param_data = loadmat('ex8_movieParams.mat')
X, Theta = param_data['X'], param_data['Theta']
n_movies, n_users = Y.shape
param = serialize(X, Theta)
learningRate = 1
X_grad, Theta_grad = deserialize(regularizedGradient(param, Y, R, 10, learningRate), n_movies, n_users, 10)
print(X_grad, Theta_grad)
[[-5.21315594 2.0591285 -5.68148384 ... -3.95439796 3.14612528
-1.59912133]
[-3.02846323 1.41931663 -2.11758176 ... -2.85177984 1.68511329
2.08666626]
[-2.4893923 2.00068576 0.1550494 ... -3.34923876 2.41055086
4.33843977]
...
[-0.82821934 0.7917289 -0.39662935 ... -0.60746963 0.28294163
-0.71223186]
[-0.62377152 0.60121466 -1.02043496 ... -0.84313998 1.30670669
-0.10603832]
[-0.31115177 0.86705203 -0.2616062 ... -1.64900127 1.08850949
0.16318173]] [[-1.26184516 7.39696961 -0.37924484 ... -3.15312086 4.55958584
0.91278897]
[-2.08328593 2.06877489 -1.20656461 ... -4.37487155 4.62450461
1.49336864]
[ 1.71397243 1.53009129 -3.47519602 ... -5.47031706 1.46428521
0.63418576]
...
[-3.53947561 2.83086629 -1.95973324 ... -2.70464586 2.25512788
0.52946291]
[-3.50593747 0.42141628 -1.62891338 ... -5.37296895 3.1012226
3.13766426]
[-2.92779591 1.05501291 -4.62312829 ... -5.27650042 4.22109195
2.11819114]]
2.3 Learning movie recommendations
内容:创建自己的电影评分,以生成个性化推荐。有一个提供连接电影索引到其标题的文件。
main.py
import numpy as np
# open打开一个文件
f = open('movie_ids.txt', encoding='gbk', errors='ignore')
movie_list = []
for line in f:
tokens = line.strip().split(' ')
movie_list.append(' '.join(tokens[1:])) # 将电影名存入列表中
movie_list = np.array(movie_list)
print(movie_list[0])
Toy Story (1995)
2.3.1 Recommendations
内容:将自己的评级数据添加到原始数据中。训练数据,得到参数,推荐出用户可能喜欢的电影。
首先演示一下Python插入数据(非0即1,0则0)
test.py
import numpy as np
arr = np.array([
[1, 1, 1],
[1, 1, 0],
[1, 1, 0]
]).reshape(3, 3)
rate = np.array([2, 3, 0]).reshape(3, 1)
arr = np.append(rate != 0, arr, axis=1)
print(arr)
[[1 1 1 1]
[1 1 1 0]
[0 1 1 0]]
对评级进行归一化处理,并训练数据。
main.py
import numpy as np
from scipy.io import loadmat
from scipy.optimize import minimize
from costFunction import *
from regularizedContent import *
# open打开一个文件
f = open('movie_ids.txt', encoding='gbk', errors='ignore')
movie_list = []
for line in f:
tokens = line.strip().split(' ')
movie_list.append(' '.join(tokens[1:])) # 将电影名存入列表中
movie_list = np.array(movie_list)
ratings = np.zeros((1682, 1)) # 给定一些电影的评分
ratings[0] = 4
ratings[6] = 3
ratings[11] = 5
ratings[65] = 3
ratings[68] = 5
ratings[97] = 2
ratings[182] = 4
ratings[225] = 5
ratings[354] = 5
# print(ratings.shape) # (1682, 1)
# 1.我们现在成为user0
raw_data = loadmat('ex8_movies')
Y, R = raw_data['Y'], raw_data['R']
Y = np.append(ratings, Y, axis=1)
# print(Y.shape)
R = np.append(ratings != 0, R, axis=1)
# print(R.shape) # (1682, 944)
n_movies, n_users = Y.shape
n_features = 10
learningRate = 10
# 2.初始化X,Theta参数
# np.random.random((a,b))-生成a行b列的浮点数(0-1随机)
X = np.random.random((n_movies, n_features))
Theta = np.random.random((n_users, n_features))
param = serialize(X, Theta)
# print(X.shape, Theta.shape, param.shape) # (1682, 10) (944, 10) (26260,)
# 3.进行归一化
Y_mean = (Y.sum(axis=1) / R.sum(axis=1)).reshape(-1, 1)
# print(Y_mean.shape) # (1682, 1)
Y_norm = np.multiply(Y - Y_mean, R)
# print(Y_norm.shape) # (1682, 944)
# 4.训练数据
fmin = minimize(fun=regularizedCostFunction, x0=param, args=(Y_norm, R, n_features, learningRate), method='TNC',
jac=regularizedGradient)
X_trained, Theta_trained = deserialize(fmin.x, n_movies, n_users, n_features)
# print(X_trained.shape, theta_trained.shape) # (1682, 10) (944, 10)
# 5.得到训练出的数据后,给出所推荐的电影
predictions = X_trained @ Theta_trained.T
# print(predictions.shape) # (1682, 944)
Y_mean = (Y.sum(axis=1) / R.sum(axis=1))
my_preds = predictions[:, 0] + Y_mean
# print(my_preds.shape) # (1682,)
# argsort返回数组值从小到大的索引值
idx = np.argsort(my_preds)[::-1] # 降序排列
for m in movie_list[idx][:5]:
print(m) # 取前五部高分的
Santa with Muscles (1996)
Great Day in Harlem, A (1994)
Entertaining Angels: The Dorothy Day Story (1996)
They Made Me a Criminal (1939)
Saint of Fort Washington, The (1993)