1 Introduction
1.1 内容
上一章是对一个unknown MDP进行value function的预测,相当于policy evaluation。这一章是对unknown MDP找到一个最优的policy, optimise value function.
1.2 On and Off-Policy Learning
On-policy learning
- learn on the job
- learn about policy
π
\pi
π from experience sampled from
π
\pi
π
Off-policy learning - look over someone’s shoulder
- learn about policy π \pi π from experience sampled from μ \mu μ
2 On-policy Monte-Carlo Control
一般的policy iteraion的框架
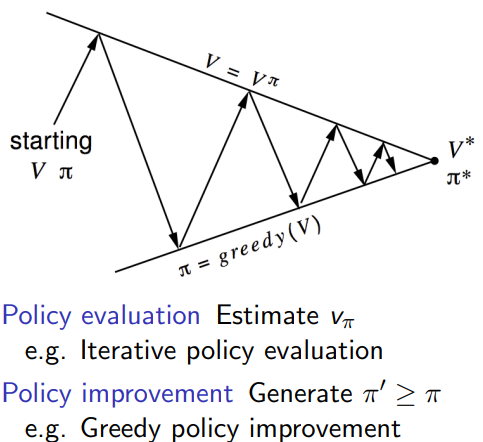
2.1 mc条件下如何进行policy iteration
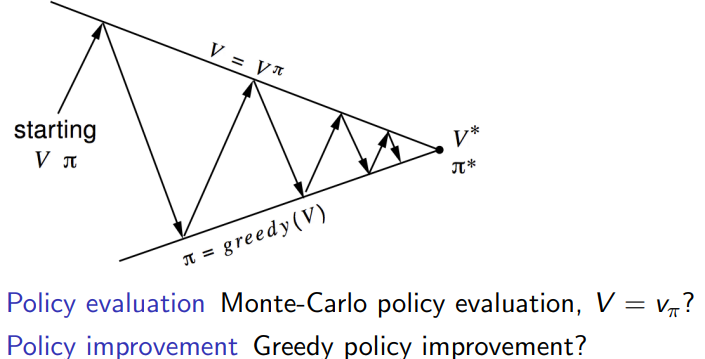
之前在做Policy evaluation的时候,用的是state value function
V
π
V_{\pi}
Vπ.
切换到Greedy policy improvement, 还是用这个吗?主要问题是状态转移矩阵和reward都不知道,
选择Q(s,a)最起码不需要显式的知道状态转移矩阵和reward。
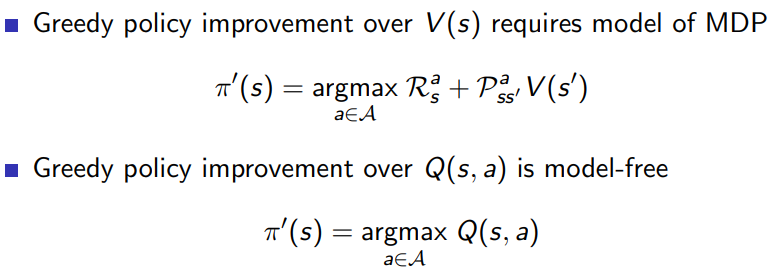
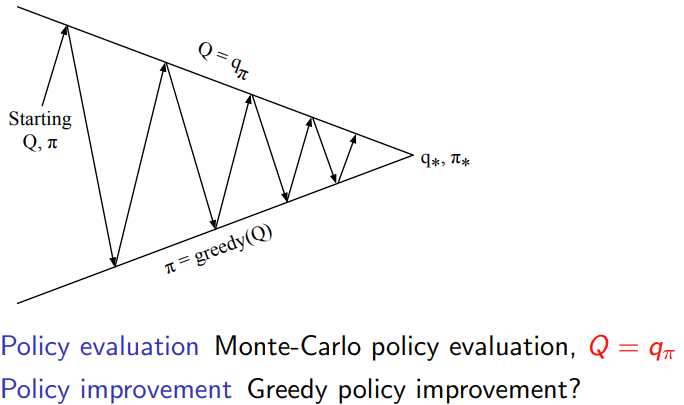
有一些方法可以学习Q(s,a),通过过往经验根据统计的方法去估计,或者神经网络去估计。
蒙特卡洛方法(Monte Carlo Methods):这种方法通过从实际经验中采样完整的episode,并利用该episode的平均回报来估计Q(s, a)。蒙特卡洛方法对每个状态-动作对都进行独立的评估,并且只在episode结束时更新Q值。
Temporal-Difference(TD)学习:TD学习是一种在线学习方法,它在每一步都更新Q值。这种方法在每次状态转换(s, a, r, s’)时更新Q值,使用TD误差(即当前奖励加上下一个状态-动作对的折扣Q值减去当前状态-动作对的Q值)。
Q-learning:Q-learning是一种TD学习方法,但它学习的是一个估计的最优Q值函数,而不是策略的Q值。在每个时间步,Q-learning更新Q值时,会采用greedy策略选择下一个状态的最大Q值,而不是使用当前策略选择的Q值。

2.2 exploration
只采用greedy action selection在MDP条件下,显然是最佳的;对于POMDP存在一些问题了。
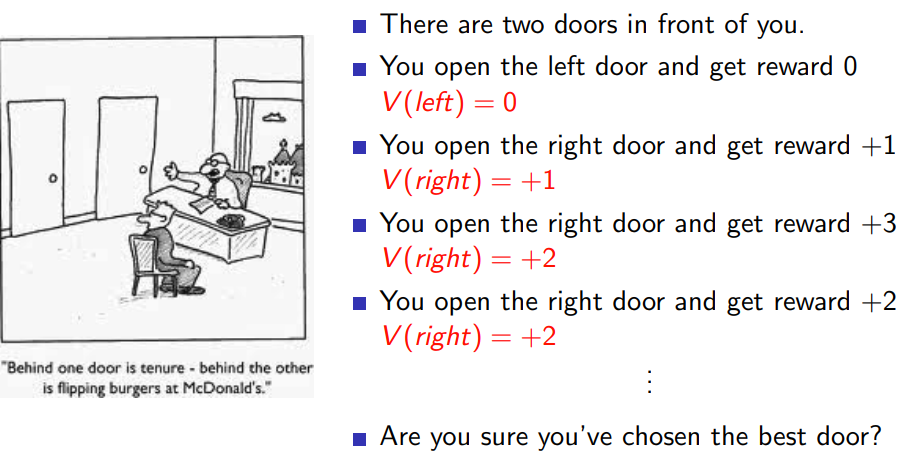
2.2.1 ϵ − \epsilon- ϵ−Greedy exploration

用这种方法来解决driving home policy iteration的问题
import numpy as np
n_states = 4
n_actions = 2
n_episodes = 5000
epsilon = 0.1
gamma = 0.9
# Step function
def step(state, action):
if action == 0: # Accelerate
next_state = max(state - 1, 0)
else: # Decelerate
next_state = min(state + 1, n_states - 1)
reward = -1 if next_state != 0 else 0
return next_state, reward
# Epsilon-greedy policy
def epsilon_greedy_policy(Q, state, epsilon):
if np.random.rand() < epsilon:
return np.random.randint(n_actions)
else:
return np.argmax(Q[state, :])
# Monte Carlo Policy Iteration with epsilon-greedy policy
Q = np.zeros((n_states, n_actions))
returns = np.zeros((n_states, n_actions))
counts = np.zeros((n_states, n_actions))
for _ in range(n_episodes):
state = n_states - 1
episode = []
while state != 0:
action = epsilon_greedy_policy(Q, state, epsilon)
next_state, reward = step(state, action)
episode.append((state, action, reward))
state = next_state
G = 0
for t in reversed(range(len(episode))):
state, action, reward = episode[t]
G = gamma * G + reward
counts[state, action] += 1
returns[state, action] += G
Q[state, action] = returns[state, action] / counts[state, action]
policy = np.argmax(Q, axis=1)
print("Optimal policy:", policy)
这里代码采用了一种隐士的方法来实现 ϵ − \epsilon- ϵ−exploration
2.2.2 ϵ − \epsilon- ϵ−policy improvement

确定一个完整的MC pipeline
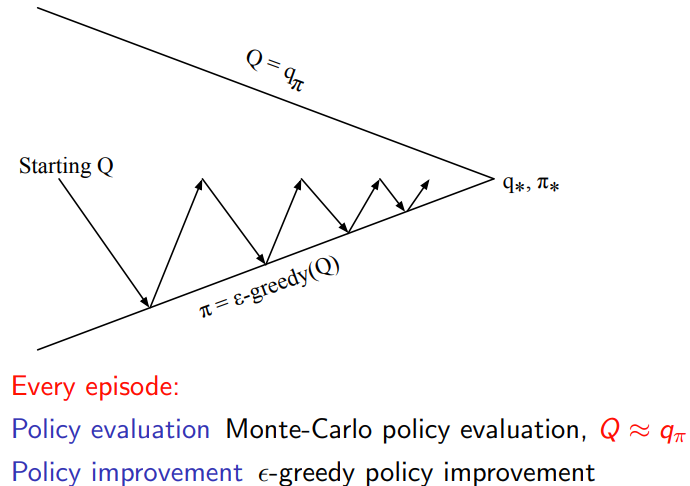
2.2.3 GLIE
Greedy in the Limit with Infinite Exploration (GLIE)
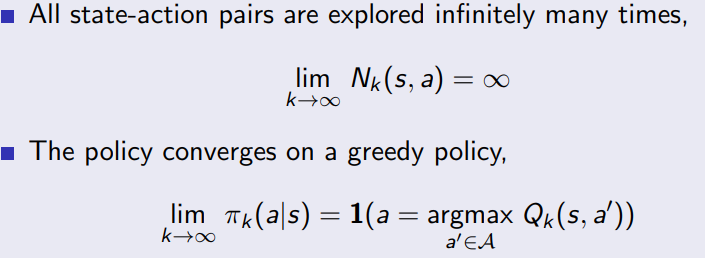
GLIE Monte-Carlo Control(Greedy in the Limit with Infinite Exploration,具有无限探索的极限贪心)和ε-greedy策略都是强化学习中用于平衡探索和利用的策略。这两种方法之间的区别和联系如下:
1.GLIE Monte-Carlo Control是一种强化学习算法,它使用一种特殊的探索策略来确保所有状态-动作对都被无限次探索。具体来说,GLIE算法要求在算法执行过程中逐渐减小探索率ε,使得在无限时间内,探索率趋向于0。这意味着,随着时间的推移,GLIE Monte-Carlo Control将越来越倾向于选择最优动作。
2.ε-greedy策略是一种常用的探索-利用平衡策略。它以ε的概率随机选择一个动作(探索),以1-ε的概率选择具有最高Q值的动作(利用)。ε-greedy策略可以用在各种强化学习算法中,包括GLIE Monte-Carlo Control。
总的来说,GLIE Monte-Carlo Control是一种强化学习算法,而ε-greedy策略是一种在该算法中可以使用的探索-利用平衡策略。在GLIE Monte-Carlo Control中,ε-greedy策略需要满足特定条件(即逐渐降低探索率ε),以确保在算法收敛时找到最优策略。
对于
ϵ
\epsilon
ϵ逐渐收敛到0的形式,就是GLIE
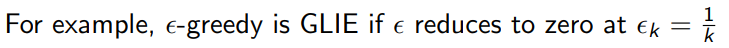

用GLIE重新实现刚才的代码
import numpy as np
n_states = 6
n_actions = 2
n_episodes = 5000
gamma = 0.9
# step function
def step(state, action):
if action == 0: # drive
next_state = min(state + np.random.randint(1, 7), n_states - 1)
reward = -1
else: # wait
next_state = state
reward = -2
return next_state, reward
# epsilon-greedy action selection
def epsilon_greedy(Q, state, epsilon):
if np.random.rand() < epsilon:
return np.random.randint(n_actions)
else:
return np.argmax(Q[state, :])
# GLIE Monte-Carlo Control
Q = np.zeros((n_states, n_actions))
returns = {}
counts = np.ones((n_states, n_actions))
for episode in range(n_episodes):
state = 0
trajectory = []
while state != n_states - 1:
epsilon = 1 / np.min(counts[state, :])
action = epsilon_greedy(Q, state, epsilon)
next_state, reward = step(state, action)
trajectory.append((state, action, reward))
state = next_state
G = 0
for t in reversed(range(len(trajectory))):
state, action, reward = trajectory[t]
G = gamma * G + reward
# Check if this state-action pair is first visited in this episode
if not any(x[0] == state and x[1] == action for x in trajectory[:t]):
if (state, action) not in returns:
returns[(state, action)] = []
returns[(state, action)].append(G)
Q[state, action] = np.mean(returns[(state, action)])
counts[state, action] += 1
print("Q-values:")
print(Q)
policy = np.argmax(Q, axis=1)
print("Policy:", policy)

3 On-policy Temporal-Difference Learning
3.1 MC vs TD control
TD 相对于 MC的优势
- Lower variance
- Online
- Incomplete sequences
Natural idea: use TD instead of MC on our control loop - Apply TD to Q(S, A)
- Use ϵ − \epsilon- ϵ−greedy policy improvement
- Update every time-step
3.2 Sarsa( λ \lambda λ)
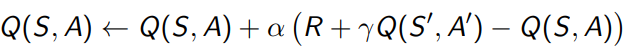
对比一下TD(\lambda)的policy evaluation的公式
E
0
(
s
)
=
0
E
t
(
s
)
=
γ
λ
E
t
−
1
(
s
)
+
1
(
s
t
=
s
)
δ
t
=
R
t
+
1
+
γ
V
(
S
t
+
1
)
−
V
(
S
t
)
V
(
s
)
=
V
(
s
)
+
α
∗
δ
t
∗
E
t
(
s
)
\begin{aligned} E_0(s)&=0\\ E_t(s)&=\gamma \lambda E_{t-1}(s)+1(s_t=s) \\ \delta_t &= R_{t+1}+\gamma V(S_{t+1})-V(S_t) \\ V(s) &=V(s)+ \alpha * \delta_t * E_t(s) \end{aligned}
E0(s)Et(s)δtV(s)=0=γλEt−1(s)+1(st=s)=Rt+1+γV(St+1)−V(St)=V(s)+α∗δt∗Et(s)
现在不用state value function,更换成
V
(
S
t
)
=
Q
(
S
,
A
)
V
(
S
′
)
=
Q
(
S
′
,
A
′
)
\begin{aligned} V(S_t) &=Q(S,A) \\ V(S') & = Q(S', A') \end{aligned}
V(St)V(S′)=Q(S,A)=Q(S′,A′)
实现之前的driving home的代码

import numpy as np
n_states = 6
n_actions = 2
n_episodes = 5000
gamma = 0.9
alpha = 0.1
_lambda = 0.9
# step function
def step(state, action):
if action == 0: # drive
next_state = min(state + np.random.randint(1, 7), n_states - 1)
reward = -1
else: # wait
next_state = state
reward = -2
return next_state, reward
# epsilon-greedy action selection
def epsilon_greedy(Q, state, epsilon):
if np.random.rand() < epsilon:
return np.random.randint(n_actions)
else:
return np.argmax(Q[state, :])
# Sarsa(lambda) algorithm
Q = np.zeros((n_states, n_actions))
counts = np.ones((n_states, n_actions))
for episode in range(n_episodes):
state = 0
epsilon = 1 / np.min(counts[state, :])
action = epsilon_greedy(Q, state, epsilon)
E = np.zeros((n_states, n_actions))
while state != n_states - 1:
next_state, reward = step(state, action)
epsilon = 1 / np.min(counts[next_state, :])
next_action = epsilon_greedy(Q, next_state, epsilon)
delta = reward + gamma * Q[next_state, next_action] - Q[state, action]
E[state, action] = E[state, action] * (gamma * _lambda) + 1
Q += alpha * delta * E
counts[state, action] += 1
E *= gamma * _lambda
state, action = next_state, next_action
print("Q-values:")
print(Q)
policy = np.argmax(Q, axis=1)
print("Policy:", policy)
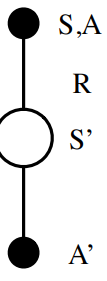
3.2.1 converges

forward view sarsa,平衡当前的reward和未来的影响Q

backward view, 和
T
D
(
λ
)
TD(\lambda)
TD(λ)类似

4 Off-Policy Learning
4.1 离线学习的作用和意义

Off-policy学习是强化学习中的一种方法,指的是在学习过程中,学习者并不完全遵循当前的策略进行决策。换句话说,它可以从其他策略生成的数据中学习,而不仅仅是从当前策略中学习。这种学习方法的优点是能够在训练过程中有效地利用历史数据,并且有助于学习更强大、更稳定的策略。
import numpy as np
import gym
# 创建FrozenLake-v1环境
env = gym.make("FrozenLake-v1")
# 初始化 Q-table
num_states = env.observation_space.n
num_actions = env.action_space.n
q_table = np.zeros((num_states, num_actions))
# 超参数设置
num_episodes = 5000
alpha = 0.1 # 学习率
gamma = 0.99 # 折扣因子
epsilon = 1 # 探索率
min_epsilon = 0.01 # 最小探索率
decay_rate = 0.999 # 探索率衰减率
# Q-learning算法
for episode in range(num_episodes):
state = env.reset()
done = False
if isinstance(state, tuple):
state = state[0]
while not done:
# 采用epsilon-greedy策略选择动作
if np.random.uniform(0, 1) < epsilon:
action = env.action_space.sample() # 随机选择一个动作
else:
action = np.argmax(q_table[state]) # 选择Q值最大的动作
# 执行动作,观察新状态和奖励
next_state, reward, done, _, _ = env.step(action)
# 更新 Q-table
q_table[state, action] += alpha * (reward + gamma * np.max(q_table[next_state]) - q_table[state, action])
# 更新状态
state = next_state
# 更新探索率
epsilon = max(min_epsilon, epsilon * decay_rate)
# 输出训练后的 Q-table
print("训练后的Q-table:")
print(q_table)
# 测试训练好的智能体
num_test_episodes = 3
for episode in range(num_test_episodes):
state = env.reset()
if isinstance(state, tuple):
state = state[0]
done = False
print(f"\n测试智能体, 试验 {episode + 1}:")
while not done:
action = np.argmax(q_table[state]) # 选择Q值最大的动作
next_state, _, done, _, _ = env.step(action)
env.render() # 渲染环境
state = next_state
env.close()
对比sarsa(0)的Python代码
import numpy as np
import gym
# 创建FrozenLake-v1环境
env = gym.make("FrozenLake-v1")
# 初始化 Q-table
num_states = env.observation_space.n
num_actions = env.action_space.n
q_table = np.zeros((num_states, num_actions))
# 超参数设置
num_episodes = 5000
alpha = 0.1 # 学习率
gamma = 0.99 # 折扣因子
epsilon = 1 # 探索率
min_epsilon = 0.01 # 最小探索率
decay_rate = 0.999 # 探索率衰减率
# SARSA(0)算法
for episode in range(num_episodes):
state = env.reset()
done = False
# 使用epsilon-greedy策略选择初始动作
if np.random.uniform(0, 1) < epsilon:
action = env.action_space.sample() # 随机选择一个动作
else:
action = np.argmax(q_table[state]) # 选择Q值最大的动作
while not done:
# 执行动作,观察新状态和奖励
next_state, reward, done, _ = env.step(action)
# 使用epsilon-greedy策略选择下一个动作
if np.random.uniform(0, 1) < epsilon:
next_action = env.action_space.sample() # 随机选择一个动作
else:
next_action = np.argmax(q_table[next_state]) # 选择Q值最大的动作
# 更新 Q-table
q_table[state, action] += alpha * (reward + gamma * q_table[next_state, next_action] - q_table[state, action])
# 更新状态和动作
state = next_state
action = next_action
# 更新探索率
epsilon = max(min_epsilon, epsilon * decay_rate)
# 输出训练后的 Q-table
print("训练后的Q-table:")
print(q_table)
# 测试训练好的智能体
num_test_episodes = 3
for episode in range(num_test_episodes):
state = env.reset()
done = False
print(f"\n测试智能体, 试验 {episode + 1}:")
while not done:
action = np.argmax(q_table[state]) # 选择Q值最大的动作
next_state, _, done, _ = env.step(action)
env.render() # 渲染环境
state = next_state
env.close()
代码对比可以看出
# sarsa(0)
# 更新 Q-table
q_table[state, action] += alpha * (reward + gamma * q_table[next_state, next_action] - q_table[state, action])
# 更新状态和动作
state = next_state
action = next_action
# 更新探索率
epsilon = max(min_epsilon, epsilon * decay_rate)
# Q-learning
# 更新 Q-table
q_table[state, action] += alpha * (reward + gamma * np.max(q_table[next_state]) - q_table[state, action])
# 更新状态
state = next_state
# 更新探索率
epsilon = max(min_epsilon, epsilon * decay_rate)
Q-learning的off-policy特性体现在它能从其他策略生成的经验中学习。在Q-learning中,更新Q值时我们考虑了最大化下一状态的Q值,而不是基于当前策略实际采取的动作。这意味着Q-learning在更新过程中既考虑了当前策略下的动作,也考虑了其他策略下的动作。这使得Q-learning能够学习到最优策略,而不仅仅局限于当前策略。
在更新Q-table时,我们使用了np.max(q_table[next_state])来计算下一状态的最大Q值。这个最大Q值可能来自于其他策略,而不仅仅是当前的策略。这就是Q-learning如何体现off-policy特性的。
# 执行动作,观察新状态和奖励
next_state, reward, done, _ = env.step(action)
# 更新 Q-table
q_table[state, action] += alpha * (reward + gamma * np.max(q_table[next_state]) - q_table[state, action])
4.2 importance sampling
4.2.1 definition
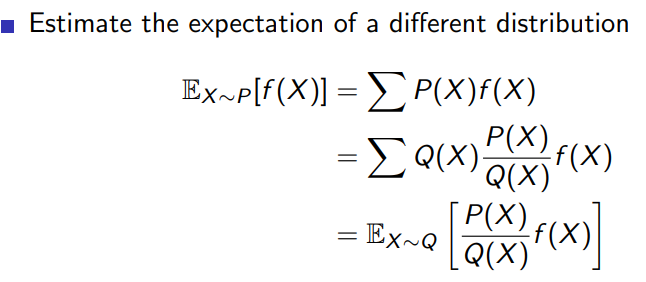
4.2.2 importance sampling for off-policy Monte-Carlo
在强化学习中,重要性采样(Importance Sampling)是一种数学技术,用于从一个分布中估计另一个分布的期望值。在强化学习的背景下,重要性采样通常用于从一个策略(行为策略,称为b)中生成的经验样本来估计另一个策略(目标策略,称为π)的期望回报。这在off-policy学习算法中尤为重要,因为我们需要从一个策略的经验中学习另一个策略。
重要性采样的基本思想是通过对目标策略和行为策略的概率比值(称为重要性采样比率)进行加权,来修正从行为策略生成的样本。这样一来,我们就可以使用这些加权样本来估计目标策略的期望回报。
设想我们有一个序列(轨迹):s_0, a_0, r_1, s_1, a_1, r_2, …, s_{T-1}, a_{T-1}, r_T, s_T,其中s_i表示状态,a_i表示动作,r_{i+1}表示奖励。我们可以计算这个序列在目标策略和行为策略下的概率,分别表示为P_π和P_b。重要性采样比率(IS)定义为目标策略和行为策略概率的比值:
IS = P π P b \text{IS} = \frac{P_\pi}{P_b} IS=PbPπ
在强化学习中,我们通常使用累积折扣回报(G_t)来评估策略。为了估计目标策略的累积折扣回报,我们可以使用行为策略生成的轨迹和重要性采样比率来加权:
E [ G t π ] ≈ 1 N ∑ i = 1 N ( G t b ⋅ IS ) \mathbb{E}[G_t^\pi] \approx \frac{1}{N} \sum_{i=1}^{N} \left( G_t^b \cdot \text{IS} \right) E[Gtπ]≈N1i=1∑N(Gtb⋅IS)
其中N表示轨迹数量,G_t^{π} 表示目标策略的累积折扣回报,G_t^b表示行为策略的累积折扣回报。
累积折扣回报
G
t
b
G_t^b
Gtb,可以通过累计回报的定义,或者MC算法进行计算
G
t
b
=
r
t
+
1
+
γ
r
t
+
2
+
γ
2
r
t
+
3
+
⋯
+
γ
T
−
t
−
1
r
T
G_t^b = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots + \gamma^{T-t-1} r_T
Gtb=rt+1+γrt+2+γ2rt+3+⋯+γT−t−1rT
G_tπ表示在时间步t开始,根据目标策略π在未来所有时间步中获得的累积折扣回报。直接计算G_tπ可能很困难,因为我们可能没有关于目标策略π的经验数据。然而,我们可以使用重要性采样(Importance Sampling)来间接估计G_t^π。通过利用行为策略b生成的轨迹和重要性采样比率(IS),我们可以计算加权的累积折扣回报,从而估计目标策略π的期望回报。
在计算G_tπ时,我们需要先计算G_tb,然后使用重要性采样比率(IS)对其进行加权。重要性采样比率是目标策略π和行为策略b在每个时间步上的概率比值的乘积。我们可以通过以下方式计算G_t^π的估计值:
E [ G t π ] ≈ 1 N ∑ i = 1 N ( G t b ⋅ IS ) \mathbb{E}[G_t^\pi] \approx \frac{1}{N} \sum_{i=1}^{N} \left( G_t^b \cdot \text{IS} \right) E[Gtπ]≈N1i=1∑N(Gtb⋅IS)
其中,N表示轨迹数量,G_t^b表示行为策略b的累积折扣回报,IS表示重要性采样比率。
为了计算重要性采样比率,我们需要分别计算目标策略π和行为策略b在每个时间步上采取相应动作的概率。设π(a_t|s_t)表示在状态s_t下,根据目标策略π采取动作a_t的概率,而b(a_t|s_t)表示在状态s_t下,根据行为策略b采取动作a_t的概率。那么,重要性采样比率可以通过以下公式计算:
IS
=
∏
k
=
t
T
−
1
π
(
a
k
∣
s
k
)
b
(
a
k
∣
s
k
)
\text{IS} = \prod_{k=t}^{T-1} \frac{\pi(a_k|s_k)}{b(a_k|s_k)}
IS=k=t∏T−1b(ak∣sk)π(ak∣sk)

使用一个例子,假设我们有一个简单的马尔可夫决策过程(MDP),共有两个状态A和B。在每个状态下,智能体可以采取两个动作:向左(L)或向右(R)。智能体按照行为策略b来选择动作,而我们希望估计目标策略π的期望回报。
π(A, L) = 0.9, π(A, R) = 0.1
π(B, L) = 0.5, π(B, R) = 0.5
b(A, L) = 0.5, b(A, R) = 0.5
b(B, L) = 0.7, b(B, R) = 0.3
# 定义目标策略π和行为策略b
pi = {
('A', 'L'): 0.9,
('A', 'R'): 0.1,
('B', 'L'): 0.5,
('B', 'R'): 0.5,
}
b = {
('A', 'L'): 0.5,
('A', 'R'): 0.5,
('B', 'L'): 0.7,
('B', 'R'): 0.3,
}
# 按照行为策略b生成的轨迹
trajectory = [('A', 'L'), ('B', 'R'), ('A', 'L')]
# 计算重要性采样比率
def importance_sampling_ratio(trajectory, pi, b):
is_ratio = 1.0
for state, action in trajectory:
is_ratio *= pi[state, action] / b[state, action]
return is_ratio
# 计算轨迹的重要性采样比率
is_ratio = importance_sampling_ratio(trajectory, pi, b)
print("Importance Sampling Ratio:", is_ratio)
实际工程中,概率如何获得
在实际应用中,使用重要性采样时确实需要知道行为策略(b)和目标策略(π)在每个状态下选择动作的概率。通常,这些概率可以从策略本身获得。对于离策略学习,我们在采样过程中使用行为策略,因此可以在生成轨迹时记录这些概率。
对于目标策略(π),我们通常根据当前的价值函数或Q函数来确定。例如,在Q-Learning中,我们希望学习最优策略,因此目标策略是在每个状态下选择具有最高Q值的动作。这种情况下,目标策略是确定性的,所以在给定状态下选择最优动作的概率为1,其他动作的概率为0。
行为策略(b)通常更容易获取,因为我们在生成轨迹时使用它来选择动作。例如,在使用Epsilon-greedy策略时,我们知道在给定状态下选择最优动作的概率为1 - epsilon + epsilon / n_actions,而选择其他动作的概率为epsilon / n_actions。我们可以在采样过程中记录这些概率。
def generate_trajectory_with_behavior_policy(env, q_table, epsilon):
trajectory = []
state = env.reset()
done = False
while not done:
action = epsilon_greedy_policy(state, q_table, epsilon)
# 计算行为策略概率
optimal_action = np.argmax(q_table[state])
if action == optimal_action:
behavior_prob = 1 - epsilon + epsilon / n_actions
else:
behavior_prob = epsilon / n_actions
next_state, reward, done, _ = env.step(action)
trajectory.append((state, action, reward, behavior_prob))
state = next_state
return trajectory
再来看一个importance sampling 和expect sarsa结合起来的例子
import numpy as np
import gym
# 初始化环境
env = gym.make('FrozenLake-v1')
# 初始化参数
n_states = env.observation_space.n
n_actions = env.action_space.n
alpha = 0.1 # 学习率
gamma = 0.99 # 折扣因子
epsilon = 0.1 # Epsilon-greedy策略参数
episodes = 20000 # 迭代次数
# 初始化Q表
q_table = np.zeros((n_states, n_actions))
# Epsilon-greedy策略
def epsilon_greedy_policy(state, q_table, epsilon):
if np.random.rand() < epsilon:
return np.random.randint(n_actions)
else:
return np.argmax(q_table[state])
# 通过重要性采样更新Q值
def update_q_table_with_importance_sampling(state, action, reward, next_state, q_table, alpha, gamma, epsilon):
# 使用Q-Learning选择下一个动作
next_action = np.argmax(q_table[next_state])
# 使用Epsilon-greedy策略选择下一个动作
behavior_next_action = epsilon_greedy_policy(next_state, q_table, epsilon)
# 计算目标策略和行为策略的概率
target_policy_prob = 1.0 if action == next_action else 0.0
behavior_policy_prob = 1 - epsilon + epsilon / n_actions if action == behavior_next_action else epsilon / n_actions
# 计算重要性采样比率
importance_sampling_ratio = target_policy_prob / behavior_policy_prob
# 计算TD目标和TD误差
td_target = reward + gamma * q_table[next_state, next_action]
td_error = td_target - q_table[state, action]
# 使用重要性采样更新Q值
q_table[state, action] += alpha * importance_sampling_ratio * td_error
# 开始学习
for episode in range(episodes):
state = env.reset()
done = False
while not done:
# 选择动作
action = epsilon_greedy_policy(state, q_table, epsilon)
# 执行动作并观察结果
next_state, reward, done, _ = env.step(action)
# 更新Q表
update_q_table_with_importance_sampling(state, action, reward, next_state, q_table, alpha, gamma, epsilon)
# 更新状态
state = next_state
print("Q-Table:")
print(q_table)
在来看一下q-table的公式
q
table
(
s
t
,
a
t
)
←
q
table
(
s
t
,
a
t
)
+
α
⋅
ρ
⋅
TD
error
q_{\text{table}}(s_t, a_t) \leftarrow q_{\text{table}}(s_t, a_t) + \alpha \cdot \rho \cdot \text{TD}_\text{error}
qtable(st,at)←qtable(st,at)+α⋅ρ⋅TDerror
TDtarget
=
r
t
+
1
+
γ
⋅
E
a
t
+
1
∼
π
[
q
table
(
s
t
+
1
,
a
t
+
1
)
]
\text{TD}\text{target} = r_{t+1} + \gamma \cdot \mathbb{E}_{a_{t+1} \sim \pi}[q_{\text{table}}(s_{t+1}, a_{t+1})]
TDtarget=rt+1+γ⋅Eat+1∼π[qtable(st+1,at+1)]
在这个公式中,TD目标表示我们希望学习到的理想Q值,它是由当前奖励加上折扣期望回报组成的。在更新Q值时,我们会根据TD目标和当前Q值之间的差异(即TD误差)来调整Q值。
![[oeasy]python0050_动态类型_静态类型_编译_运行](https://img-blog.csdnimg.cn/img_convert/0ec95436f367102609e79deec2ee1b5a.png)




![[JAVA EE]创建Servlet——继承HttpServlet类笔记2](https://img-blog.csdnimg.cn/63dec33eb8fb43078f994eaccca3c93f.png)
![[前端基础]websocket协议](https://img-blog.csdnimg.cn/8d13bc87c4854523bf94b119db37b7e3.png)