背景
前面已经出了一系列的文章来介绍大模型、多模态、生成模型。这篇文章会从更微观和更贴近实际工作的角度下手。会给大家介绍下前面讲到的diffuiosn model具体怎么来实现。文章结构如下:
1.介绍Diffusion Model包括哪些零部件,这些零部件衔接关系
2.介绍介绍每部分零件的核心代码实现
3.介绍如何把这些零部件挂载到框架变成一个系统
4.小结部分
宏观模型介绍
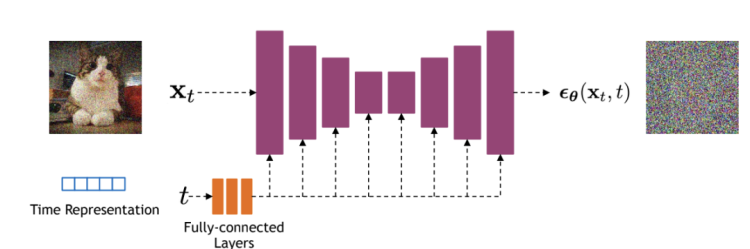
上面的图是Diffusion Model训练过程中,一个step输入、输出、网络结构。
1.输入包括了:
a.代表这是第几个step的Time Representation
b.上图轮合成图
2.预测噪声的网络就是Unet
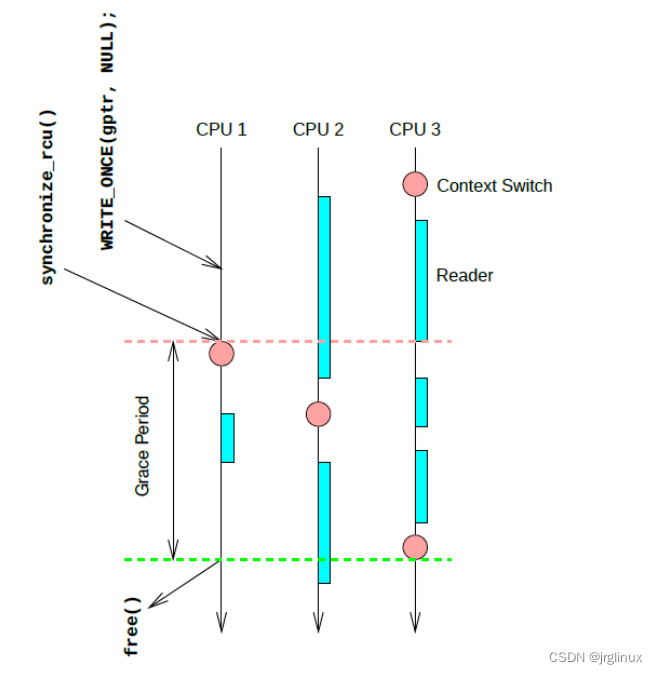
3.用过sd webui的用户应该对**schedule,如果看上面图,没发现这个**schedule在哪,那这东西是哪个部件呢,这部分李宏毅老师的视频里讲的比较清楚,下面图是从他视频里面截去处来的。
**schedule其实是在一个step中额外加进来的噪声(下图黄色Z)。加这部分原因个人猜测,是对随机生成过程这个生成流程的概率分布假设。如果知识用预测的噪声作为加噪,整个生成的链路就是固定的,只有每个step里面生成分布是符合一定分布的。为了保证生成链路是符合一定分布,加入噪声来做采样,让生成链路不是固定的,而是符合一定概率分布的。

代码实现
1.Time Representation
第几步就是用一个向量来表示,具体实现如下面代码
def timestep_embedding(timesteps, dim, max_period=10000):
"""
Create sinusoidal timestep embeddings.
:param timesteps: a 1-D Tensor of N indices, one per batch element.
These may be fractional.
:param dim: the dimension of the output.
:param max_period: controls the minimum frequency of the embeddings.
:return: an [N x dim] Tensor of positional embeddings.
"""
half = dim // 2
freqs = th.exp(
-math.log(max_period) * th.arange(start=0, end=half, dtype=th.float32) / half
).to(device=timesteps.device)
args = timesteps[:, None].float() * freqs[None]
embedding = th.cat([th.cos(args), th.sin(args)], dim=-1)
if dim % 2:
embedding = th.cat([embedding, th.zeros_like(embedding[:, :1])], dim=-1)
return embeddingtime representation是要输入到unet模型里面的,接在residual block,衔接部分代码如下:
class TimestepBlock(nn.Module):
"""
Any module where forward() takes timestep embeddings as a second argument.
"""
@abstractmethod
def forward(self, x, emb):
"""
Apply the module to `x` given `emb` timestep embeddings.
"""
class TimestepEmbedSequential(nn.Sequential, TimestepBlock):
"""
A sequential module that passes timestep embeddings to the children that
support it as an extra input.
"""
def forward(self, x, emb):
for layer in self:
if isinstance(layer, TimestepBlock):
x = layer(x, emb)
else:
x = layer(x)
return x2.Unet:
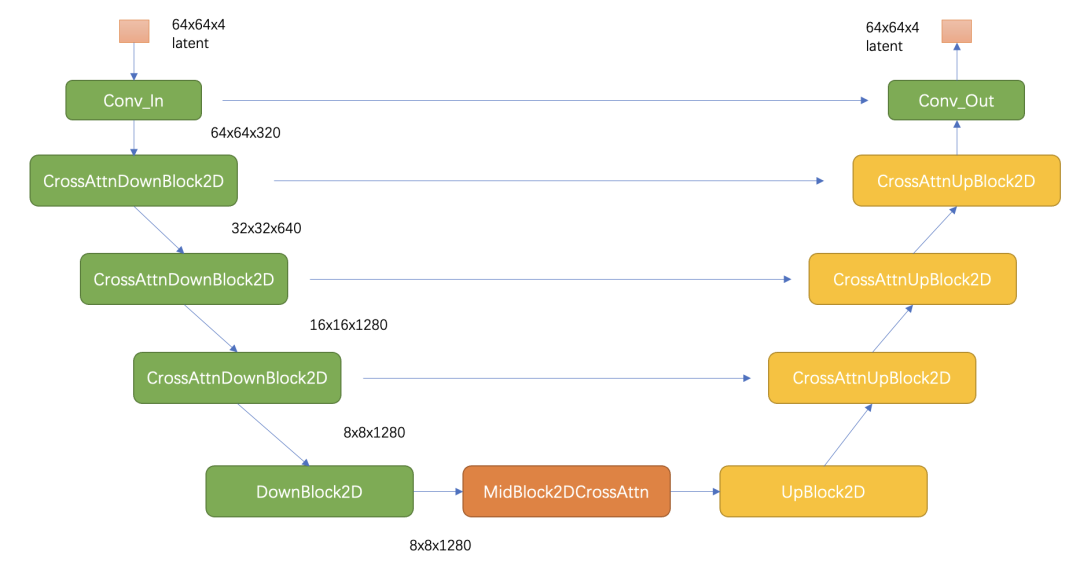
UNet,其主要结构如下图所示(这里以输入的latent为64x64x4维度为例),其中encoder部分包括3个CrossAttnDownBlock2D模块和1个DownBlock2D模块,而decoder部分包括1个UpBlock2D模块和3个CrossAttnUpBlock2D模块,中间还有一个UNetMidBlock2DCrossAttn模块。encoder和decoder两个部分是完全对应的,中间存在skip connection。注意3个CrossAttnDownBlock2D模块最后均有一个2x的downsample操作,而DownBlock2D模块是不包含下采样的。
其中CrossAttnDownBlock2D模块的主要结构如下图所示,text condition将通过CrossAttention模块嵌入进来,此时Attention的query是UNet的中间特征,而key和value则是text embeddings。
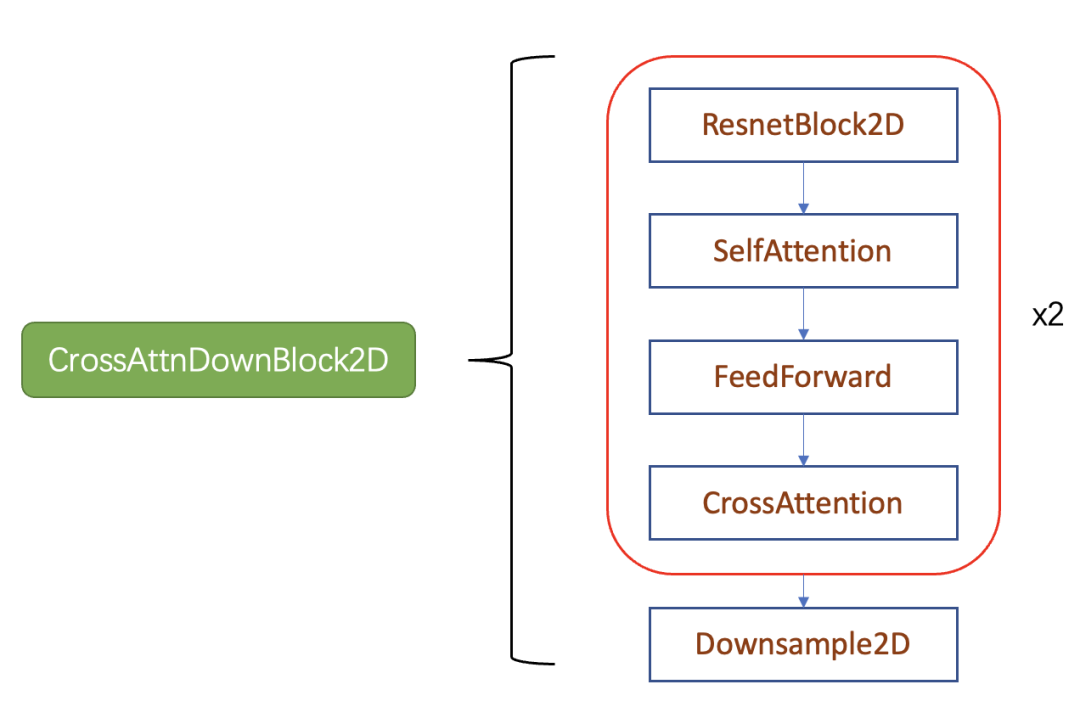
如上图所示,每个cross attention block其实就是time step、图信息融合的模块,这个模块包括了resnet block组件、selfattention组件、feed forward、crossattention组件。下面会具体介绍这些组件如何实现:
U-Net的核心模块是residual block,它包含两个卷积层以及shortcut,同时也要引入time embedding,这里额外定义了一个linear层来将time embedding变换为和特征维度一致,第一conv之后通过加上time embedding来编码time:
class ResBlock(TimestepBlock):
"""
A residual block that can optionally change the number of channels.
:param channels: the number of input channels.
:param emb_channels: the number of timestep embedding channels.
:param dropout: the rate of dropout.
:param out_channels: if specified, the number of out channels.
:param use_conv: if True and out_channels is specified, use a spatial
convolution instead of a smaller 1x1 convolution to change the
channels in the skip connection.
:param dims: determines if the signal is 1D, 2D, or 3D.
:param use_checkpoint: if True, use gradient checkpointing on this module.
"""
def __init__(
self,
channels,
emb_channels,
dropout,
out_channels=None,
use_conv=False,
use_scale_shift_norm=False,
dims=2,
use_checkpoint=False,
):
super().__init__()
self.channels = channels
self.emb_channels = emb_channels
self.dropout = dropout
self.out_channels = out_channels or channels
self.use_conv = use_conv
self.use_checkpoint = use_checkpoint
self.use_scale_shift_norm = use_scale_shift_norm
#第一层卷积
self.in_layers = nn.Sequential(
normalization(channels),
SiLU(),
conv_nd(dims, channels, self.out_channels, 3, padding=1),
)
#把time step emedding注入进来
self.emb_layers = nn.Sequential(
SiLU(),
linear(
emb_channels,
2 * self.out_channels if use_scale_shift_norm else self.out_channels,
),
)
#第二层卷积
self.out_layers = nn.Sequential(
normalization(self.out_channels),
SiLU(),
nn.Dropout(p=dropout),
zero_module(
conv_nd(dims, self.out_channels, self.out_channels, 3, padding=1)
),
)
if self.out_channels == channels:
self.skip_connection = nn.Identity()
elif use_conv:
self.skip_connection = conv_nd(
dims, channels, self.out_channels, 3, padding=1
)
else:
self.skip_connection = conv_nd(dims, channels, self.out_channels, 1)
def forward(self, x, emb):
"""
Apply the block to a Tensor, conditioned on a timestep embedding.
:param x: an [N x C x ...] Tensor of features.
:param emb: an [N x emb_channels] Tensor of timestep embeddings.
:return: an [N x C x ...] Tensor of outputs.
"""
return checkpoint(
self._forward, (x, emb), self.parameters(), self.use_checkpoint
)
def _forward(self, x, emb):
h = self.in_layers(x)
emb_out = self.emb_layers(emb).type(h.dtype)
while len(emb_out.shape) < len(h.shape):
emb_out = emb_out[..., None]
if self.use_scale_shift_norm:
out_norm, out_rest = self.out_layers[0], self.out_layers[1:]
scale, shift = th.chunk(emb_out, 2, dim=1)
h = out_norm(h) * (1 + scale) + shift
h = out_rest(h)
else:
h = h + emb_out
h = self.out_layers(h)
return self.skip_connection(x) + h这里还在部分residual block引入了attention:
class AttentionBlock(nn.Module):
"""
An attention block that allows spatial positions to attend to each other.
Originally ported from here, but adapted to the N-d case.
https://github.com/hojonathanho/diffusion/blob/1e0dceb3b3495bbe19116a5e1b3596cd0706c543/diffusion_tf/models/unet.py#L66.
"""
def __init__(self, channels, num_heads=1, use_checkpoint=False):
super().__init__()
self.channels = channels
self.num_heads = num_heads
self.use_checkpoint = use_checkpoint
self.norm = normalization(channels)
self.qkv = conv_nd(1, channels, channels * 3, 1)
self.attention = QKVAttention()
self.proj_out = zero_module(conv_nd(1, channels, channels, 1))
def forward(self, x):
return checkpoint(self._forward, (x,), self.parameters(), self.use_checkpoint)
def _forward(self, x):
b, c, *spatial = x.shape
x = x.reshape(b, c, -1)
qkv = self.qkv(self.norm(x))
qkv = qkv.reshape(b * self.num_heads, -1, qkv.shape[2])
h = self.attention(qkv)
h = h.reshape(b, -1, h.shape[-1])
h = self.proj_out(h)
return (x + h).reshape(b, c, *spatial)上采样模块和下采样模块,其分别可以采用插值和stride=2的conv或者pooling来实现:
class Upsample(nn.Module):
"""
An upsampling layer with an optional convolution.
:param channels: channels in the inputs and outputs.
:param use_conv: a bool determining if a convolution is applied.
:param dims: determines if the signal is 1D, 2D, or 3D. If 3D, then
upsampling occurs in the inner-two dimensions.
"""
def __init__(self, channels, use_conv, dims=2):
super().__init__()
self.channels = channels
self.use_conv = use_conv
self.dims = dims
if use_conv:
self.conv = conv_nd(dims, channels, channels, 3, padding=1)
def forward(self, x):
assert x.shape[1] == self.channels
if self.dims == 3:
x = F.interpolate(
x, (x.shape[2], x.shape[3] * 2, x.shape[4] * 2), mode="nearest"
)
else:
x = F.interpolate(x, scale_factor=2, mode="nearest")
if self.use_conv:
x = self.conv(x)
return x
class Downsample(nn.Module):
"""
A downsampling layer with an optional convolution.
:param channels: channels in the inputs and outputs.
:param use_conv: a bool determining if a convolution is applied.
:param dims: determines if the signal is 1D, 2D, or 3D. If 3D, then
downsampling occurs in the inner-two dimensions.
"""
def __init__(self, channels, use_conv, dims=2):
super().__init__()
self.channels = channels
self.use_conv = use_conv
self.dims = dims
stride = 2 if dims != 3 else (1, 2, 2)
if use_conv:
self.op = conv_nd(dims, channels, channels, 3, stride=stride, padding=1)
else:
self.op = avg_pool_nd(stride)
def forward(self, x):
assert x.shape[1] == self.channels
return self.op(x)把上面的各组件串起来组成UNet网络:
class UNetModel(nn.Module):
"""
The full UNet model with attention and timestep embedding.
:param in_channels: channels in the input Tensor.
:param model_channels: base channel count for the model.
:param out_channels: channels in the output Tensor.
:param num_res_blocks: number of residual blocks per downsample.
:param attention_resolutions: a collection of downsample rates at which
attention will take place. May be a set, list, or tuple.
For example, if this contains 4, then at 4x downsampling, attention
will be used.
:param dropout: the dropout probability.
:param channel_mult: channel multiplier for each level of the UNet.
:param conv_resample: if True, use learned convolutions for upsampling and
downsampling.
:param dims: determines if the signal is 1D, 2D, or 3D.
:param num_classes: if specified (as an int), then this model will be
class-conditional with `num_classes` classes.
:param use_checkpoint: use gradient checkpointing to reduce memory usage.
:param num_heads: the number of attention heads in each attention layer.
"""
def __init__(
self,
in_channels,
model_channels,
out_channels,
num_res_blocks,
attention_resolutions,
dropout=0,
channel_mult=(1, 2, 4, 8),
conv_resample=True,
dims=2,
num_classes=None,
use_checkpoint=False,
num_heads=1,
num_heads_upsample=-1,
use_scale_shift_norm=False,
):
super().__init__()
if num_heads_upsample == -1:
num_heads_upsample = num_heads
self.in_channels = in_channels
self.model_channels = model_channels
self.out_channels = out_channels
self.num_res_blocks = num_res_blocks
self.attention_resolutions = attention_resolutions
self.dropout = dropout
self.channel_mult = channel_mult
self.conv_resample = conv_resample
self.num_classes = num_classes
self.use_checkpoint = use_checkpoint
self.num_heads = num_heads
self.num_heads_upsample = num_heads_upsample
#time embbding
time_embed_dim = model_channels * 4
self.time_embed = nn.Sequential(
linear(model_channels, time_embed_dim),
SiLU(),
linear(time_embed_dim, time_embed_dim),
)
if self.num_classes is not None:
self.label_emb = nn.Embedding(num_classes, time_embed_dim)
#下采样模块
self.input_blocks = nn.ModuleList(
[
TimestepEmbedSequential(
conv_nd(dims, in_channels, model_channels, 3, padding=1)
)
]
)
input_block_chans = [model_channels]
ch = model_channels
ds = 1
for level, mult in enumerate(channel_mult):
for _ in range(num_res_blocks):
layers = [
ResBlock(
ch,
time_embed_dim,
dropout,
out_channels=mult * model_channels,
dims=dims,
use_checkpoint=use_checkpoint,
use_scale_shift_norm=use_scale_shift_norm,
)
]
ch = mult * model_channels
if ds in attention_resolutions:
layers.append(
AttentionBlock(
ch, use_checkpoint=use_checkpoint, num_heads=num_heads
)
)
self.input_blocks.append(TimestepEmbedSequential(*layers))
input_block_chans.append(ch)
if level != len(channel_mult) - 1:
self.input_blocks.append(
TimestepEmbedSequential(Downsample(ch, conv_resample, dims=dims))
)
input_block_chans.append(ch)
ds *= 2
#middle block(就是上面橙色模块,衔接encode和decode的部分)
self.middle_block = TimestepEmbedSequential(
ResBlock(
ch,
time_embed_dim,
dropout,
dims=dims,
use_checkpoint=use_checkpoint,
use_scale_shift_norm=use_scale_shift_norm,
),
AttentionBlock(ch, use_checkpoint=use_checkpoint, num_heads=num_heads),
ResBlock(
ch,
time_embed_dim,
dropout,
dims=dims,
use_checkpoint=use_checkpoint,
use_scale_shift_norm=use_scale_shift_norm,
),
)
#decode部分,上面图黄色部分
self.output_blocks = nn.ModuleList([])
for level, mult in list(enumerate(channel_mult))[::-1]:
for i in range(num_res_blocks + 1):
layers = [
ResBlock(
ch + input_block_chans.pop(),
time_embed_dim,
dropout,
out_channels=model_channels * mult,
dims=dims,
use_checkpoint=use_checkpoint,
use_scale_shift_norm=use_scale_shift_norm,
)
]
ch = model_channels * mult
if ds in attention_resolutions:
layers.append(
AttentionBlock(
ch,
use_checkpoint=use_checkpoint,
num_heads=num_heads_upsample,
)
)
if level and i == num_res_blocks:
layers.append(Upsample(ch, conv_resample, dims=dims))
ds //= 2
self.output_blocks.append(TimestepEmbedSequential(*layers))
self.out = nn.Sequential(
normalization(ch),
SiLU(),
zero_module(conv_nd(dims, model_channels, out_channels, 3, padding=1)),
)
3.schedule
针对每个step的训练,网络架构上看就差一个产生过程随机的schedule,下图黄色部分:

def get_named_beta_schedule(schedule_name, num_diffusion_timesteps):
"""
Get a pre-defined beta schedule for the given name.
The beta schedule library consists of beta schedules which remain similar
in the limit of num_diffusion_timesteps.
Beta schedules may be added, but should not be removed or changed once
they are committed to maintain backwards compatibility.
"""
if schedule_name == "linear":
# Linear schedule from Ho et al, extended to work for any number of
# diffusion steps.
scale = 1000 / num_diffusion_timesteps
beta_start = scale * 0.0001
beta_end = scale * 0.02
return np.linspace(
beta_start, beta_end, num_diffusion_timesteps, dtype=np.float64
)
elif schedule_name == "cosine":
return betas_for_alpha_bar(
num_diffusion_timesteps,
lambda t: math.cos((t + 0.008) / 1.008 * math.pi / 2) ** 2,
)
else:
raise NotImplementedError(f"unknown beta schedule: {schedule_name}")
def betas_for_alpha_bar(num_diffusion_timesteps, alpha_bar, max_beta=0.999):
"""
Create a beta schedule that discretizes the given alpha_t_bar function,
which defines the cumulative product of (1-beta) over time from t = [0,1].
:param num_diffusion_timesteps: the number of betas to produce.
:param alpha_bar: a lambda that takes an argument t from 0 to 1 and
produces the cumulative product of (1-beta) up to that
part of the diffusion process.
:param max_beta: the maximum beta to use; use values lower than 1 to
prevent singularities.
"""
betas = []
for i in range(num_diffusion_timesteps):
t1 = i / num_diffusion_timesteps
t2 = (i + 1) / num_diffusion_timesteps
betas.append(min(1 - alpha_bar(t2) / alpha_bar(t1), max_beta))
return np.array(betas)4.从一个step到多step
上面其实只是一个diffusion model的一个step过程,diffusion包含的是一个多step的随机过程,这部分的衔接代码如下。
class GaussianDiffusion:
"""
Utilities for training and sampling diffusion models.
Ported directly from here, and then adapted over time to further experimentation.
https://github.com/hojonathanho/diffusion/blob/1e0dceb3b3495bbe19116a5e1b3596cd0706c543/diffusion_tf/diffusion_utils_2.py#L42
:param betas: a 1-D numpy array of betas for each diffusion timestep,
starting at T and going to 1.
:param model_mean_type: a ModelMeanType determining what the model outputs.
:param model_var_type: a ModelVarType determining how variance is output.
:param loss_type: a LossType determining the loss function to use.
:param rescale_timesteps: if True, pass floating point timesteps into the
model so that they are always scaled like in the
original paper (0 to 1000).
"""
def __init__(
self,
*,
betas,
model_mean_type,
model_var_type,
loss_type,
rescale_timesteps=False,
):
self.model_mean_type = model_mean_type
self.model_var_type = model_var_type
self.loss_type = loss_type
self.rescale_timesteps = rescale_timesteps
# Use float64 for accuracy.
betas = np.array(betas, dtype=np.float64)
self.betas = betas
assert len(betas.shape) == 1, "betas must be 1-D"
assert (betas > 0).all() and (betas <= 1).all()
self.num_timesteps = int(betas.shape[0])
alphas = 1.0 - betas
self.alphas_cumprod = np.cumprod(alphas, axis=0)
self.alphas_cumprod_prev = np.append(1.0, self.alphas_cumprod[:-1])
self.alphas_cumprod_next = np.append(self.alphas_cumprod[1:], 0.0)
assert self.alphas_cumprod_prev.shape == (self.num_timesteps,)
# calculations for diffusion q(x_t | x_{t-1}) and others
self.sqrt_alphas_cumprod = np.sqrt(self.alphas_cumprod)
self.sqrt_one_minus_alphas_cumprod = np.sqrt(1.0 - self.alphas_cumprod)
self.log_one_minus_alphas_cumprod = np.log(1.0 - self.alphas_cumprod)
self.sqrt_recip_alphas_cumprod = np.sqrt(1.0 / self.alphas_cumprod)
self.sqrt_recipm1_alphas_cumprod = np.sqrt(1.0 / self.alphas_cumprod - 1)
# calculations for posterior q(x_{t-1} | x_t, x_0)
self.posterior_variance = (
betas * (1.0 - self.alphas_cumprod_prev) / (1.0 - self.alphas_cumprod)
)
# log calculation clipped because the posterior variance is 0 at the
# beginning of the diffusion chain.
self.posterior_log_variance_clipped = np.log(
np.append(self.posterior_variance[1], self.posterior_variance[1:])
)
self.posterior_mean_coef1 = (
betas * np.sqrt(self.alphas_cumprod_prev) / (1.0 - self.alphas_cumprod)
)
self.posterior_mean_coef2 = (
(1.0 - self.alphas_cumprod_prev)
* np.sqrt(alphas)
/ (1.0 - self.alphas_cumprod)
)
def q_mean_variance(self, x_start, t):
"""
Get the distribution q(x_t | x_0).
:param x_start: the [N x C x ...] tensor of noiseless inputs.
:param t: the number of diffusion steps (minus 1). Here, 0 means one step.
:return: A tuple (mean, variance, log_variance), all of x_start's shape.
"""
mean = (
_extract_into_tensor(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start
)
variance = _extract_into_tensor(1.0 - self.alphas_cumprod, t, x_start.shape)
log_variance = _extract_into_tensor(
self.log_one_minus_alphas_cumprod, t, x_start.shape
)
return mean, variance, log_variance
def q_sample(self, x_start, t, noise=None):
"""
Diffuse the data for a given number of diffusion steps.
In other words, sample from q(x_t | x_0).
:param x_start: the initial data batch.
:param t: the number of diffusion steps (minus 1). Here, 0 means one step.
:param noise: if specified, the split-out normal noise.
:return: A noisy version of x_start.
"""
if noise is None:
noise = th.randn_like(x_start)
assert noise.shape == x_start.shape
return (
_extract_into_tensor(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start
+ _extract_into_tensor(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape)
* noise
)
def q_posterior_mean_variance(self, x_start, x_t, t):
"""
Compute the mean and variance of the diffusion posterior:
q(x_{t-1} | x_t, x_0)
"""
assert x_start.shape == x_t.shape
posterior_mean = (
_extract_into_tensor(self.posterior_mean_coef1, t, x_t.shape) * x_start
+ _extract_into_tensor(self.posterior_mean_coef2, t, x_t.shape) * x_t
)
posterior_variance = _extract_into_tensor(self.posterior_variance, t, x_t.shape)
posterior_log_variance_clipped = _extract_into_tensor(
self.posterior_log_variance_clipped, t, x_t.shape
)
assert (
posterior_mean.shape[0]
== posterior_variance.shape[0]
== posterior_log_variance_clipped.shape[0]
== x_start.shape[0]
)
return posterior_mean, posterior_variance, posterior_log_variance_clipped
def p_mean_variance(
self, model, x, t, clip_denoised=True, denoised_fn=None, model_kwargs=None
):
"""
Apply the model to get p(x_{t-1} | x_t), as well as a prediction of
the initial x, x_0.
:param model: the model, which takes a signal and a batch of timesteps
as input.
:param x: the [N x C x ...] tensor at time t.
:param t: a 1-D Tensor of timesteps.
:param clip_denoised: if True, clip the denoised signal into [-1, 1].
:param denoised_fn: if not None, a function which applies to the
x_start prediction before it is used to sample. Applies before
clip_denoised.
:param model_kwargs: if not None, a dict of extra keyword arguments to
pass to the model. This can be used for conditioning.
:return: a dict with the following keys:
- 'mean': the model mean output.
- 'variance': the model variance output.
- 'log_variance': the log of 'variance'.
- 'pred_xstart': the prediction for x_0.
"""
if model_kwargs is None:
model_kwargs = {}
B, C = x.shape[:2]
assert t.shape == (B,)
model_output = model(x, self._scale_timesteps(t), **model_kwargs)
if self.model_var_type in [ModelVarType.LEARNED, ModelVarType.LEARNED_RANGE]:
assert model_output.shape == (B, C * 2, *x.shape[2:])
model_output, model_var_values = th.split(model_output, C, dim=1)
if self.model_var_type == ModelVarType.LEARNED:
model_log_variance = model_var_values
model_variance = th.exp(model_log_variance)
else:
min_log = _extract_into_tensor(
self.posterior_log_variance_clipped, t, x.shape
)
max_log = _extract_into_tensor(np.log(self.betas), t, x.shape)
# The model_var_values is [-1, 1] for [min_var, max_var].
frac = (model_var_values + 1) / 2
model_log_variance = frac * max_log + (1 - frac) * min_log
model_variance = th.exp(model_log_variance)
else:
model_variance, model_log_variance = {
# for fixedlarge, we set the initial (log-)variance like so
# to get a better decoder log likelihood.
ModelVarType.FIXED_LARGE: (
np.append(self.posterior_variance[1], self.betas[1:]),
np.log(np.append(self.posterior_variance[1], self.betas[1:])),
),
ModelVarType.FIXED_SMALL: (
self.posterior_variance,
self.posterior_log_variance_clipped,
),
}[self.model_var_type]
model_variance = _extract_into_tensor(model_variance, t, x.shape)
model_log_variance = _extract_into_tensor(model_log_variance, t, x.shape)
def process_xstart(x):
if denoised_fn is not None:
x = denoised_fn(x)
if clip_denoised:
return x.clamp(-1, 1)
return x
if self.model_mean_type == ModelMeanType.PREVIOUS_X:
pred_xstart = process_xstart(
self._predict_xstart_from_xprev(x_t=x, t=t, xprev=model_output)
)
model_mean = model_output
elif self.model_mean_type in [ModelMeanType.START_X, ModelMeanType.EPSILON]:
if self.model_mean_type == ModelMeanType.START_X:
pred_xstart = process_xstart(model_output)
else:
pred_xstart = process_xstart(
self._predict_xstart_from_eps(x_t=x, t=t, eps=model_output)
)
model_mean, _, _ = self.q_posterior_mean_variance(
x_start=pred_xstart, x_t=x, t=t
)
else:
raise NotImplementedError(self.model_mean_type)
assert (
model_mean.shape == model_log_variance.shape == pred_xstart.shape == x.shape
)
return {
"mean": model_mean,
"variance": model_variance,
"log_variance": model_log_variance,
"pred_xstart": pred_xstart,
}
def _predict_xstart_from_eps(self, x_t, t, eps):
assert x_t.shape == eps.shape
return (
_extract_into_tensor(self.sqrt_recip_alphas_cumprod, t, x_t.shape) * x_t
- _extract_into_tensor(self.sqrt_recipm1_alphas_cumprod, t, x_t.shape) * eps
)
def _predict_xstart_from_xprev(self, x_t, t, xprev):
assert x_t.shape == xprev.shape
return ( # (xprev - coef2*x_t) / coef1
_extract_into_tensor(1.0 / self.posterior_mean_coef1, t, x_t.shape) * xprev
- _extract_into_tensor(
self.posterior_mean_coef2 / self.posterior_mean_coef1, t, x_t.shape
)
* x_t
)
def _predict_eps_from_xstart(self, x_t, t, pred_xstart):
return (
_extract_into_tensor(self.sqrt_recip_alphas_cumprod, t, x_t.shape) * x_t
- pred_xstart
) / _extract_into_tensor(self.sqrt_recipm1_alphas_cumprod, t, x_t.shape)
def _scale_timesteps(self, t):
if self.rescale_timesteps:
return t.float() * (1000.0 / self.num_timesteps)
return t
def p_sample(
self, model, x, t, clip_denoised=True, denoised_fn=None, model_kwargs=None
):
"""
Sample x_{t-1} from the model at the given timestep.
:param model: the model to sample from.
:param x: the current tensor at x_{t-1}.
:param t: the value of t, starting at 0 for the first diffusion step.
:param clip_denoised: if True, clip the x_start prediction to [-1, 1].
:param denoised_fn: if not None, a function which applies to the
x_start prediction before it is used to sample.
:param model_kwargs: if not None, a dict of extra keyword arguments to
pass to the model. This can be used for conditioning.
:return: a dict containing the following keys:
- 'sample': a random sample from the model.
- 'pred_xstart': a prediction of x_0.
"""
out = self.p_mean_variance(
model,
x,
t,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
model_kwargs=model_kwargs,
)
noise = th.randn_like(x)
nonzero_mask = (
(t != 0).float().view(-1, *([1] * (len(x.shape) - 1)))
) # no noise when t == 0
sample = out["mean"] + nonzero_mask * th.exp(0.5 * out["log_variance"]) * noise
return {"sample": sample, "pred_xstart": out["pred_xstart"]}
def p_sample_loop(
self,
model,
shape,
noise=None,
clip_denoised=True,
denoised_fn=None,
model_kwargs=None,
device=None,
progress=False,
):
"""
Generate samples from the model.
:param model: the model module.
:param shape: the shape of the samples, (N, C, H, W).
:param noise: if specified, the noise from the encoder to sample.
Should be of the same shape as `shape`.
:param clip_denoised: if True, clip x_start predictions to [-1, 1].
:param denoised_fn: if not None, a function which applies to the
x_start prediction before it is used to sample.
:param model_kwargs: if not None, a dict of extra keyword arguments to
pass to the model. This can be used for conditioning.
:param device: if specified, the device to create the samples on.
If not specified, use a model parameter's device.
:param progress: if True, show a tqdm progress bar.
:return: a non-differentiable batch of samples.
"""
final = None
for sample in self.p_sample_loop_progressive(
model,
shape,
noise=noise,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
model_kwargs=model_kwargs,
device=device,
progress=progress,
):
final = sample
return final["sample"]
def p_sample_loop_progressive(
self,
model,
shape,
noise=None,
clip_denoised=True,
denoised_fn=None,
model_kwargs=None,
device=None,
progress=False,
):
"""
Generate samples from the model and yield intermediate samples from
each timestep of diffusion.
Arguments are the same as p_sample_loop().
Returns a generator over dicts, where each dict is the return value of
p_sample().
"""
if device is None:
device = next(model.parameters()).device
assert isinstance(shape, (tuple, list))
if noise is not None:
img = noise
else:
img = th.randn(*shape, device=device)
indices = list(range(self.num_timesteps))[::-1]
if progress:
# Lazy import so that we don't depend on tqdm.
from tqdm.auto import tqdm
indices = tqdm(indices)
for i in indices:
t = th.tensor([i] * shape[0], device=device)
with th.no_grad():
out = self.p_sample(
model,
img,
t,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
model_kwargs=model_kwargs,
)
yield out
img = out["sample"]
def ddim_sample(
self,
model,
x,
t,
clip_denoised=True,
denoised_fn=None,
model_kwargs=None,
eta=0.0,
):
"""
Sample x_{t-1} from the model using DDIM.
Same usage as p_sample().
"""
out = self.p_mean_variance(
model,
x,
t,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
model_kwargs=model_kwargs,
)
# Usually our model outputs epsilon, but we re-derive it
# in case we used x_start or x_prev prediction.
eps = self._predict_eps_from_xstart(x, t, out["pred_xstart"])
alpha_bar = _extract_into_tensor(self.alphas_cumprod, t, x.shape)
alpha_bar_prev = _extract_into_tensor(self.alphas_cumprod_prev, t, x.shape)
sigma = (
eta
* th.sqrt((1 - alpha_bar_prev) / (1 - alpha_bar))
* th.sqrt(1 - alpha_bar / alpha_bar_prev)
)
# Equation 12.
noise = th.randn_like(x)
mean_pred = (
out["pred_xstart"] * th.sqrt(alpha_bar_prev)
+ th.sqrt(1 - alpha_bar_prev - sigma ** 2) * eps
)
nonzero_mask = (
(t != 0).float().view(-1, *([1] * (len(x.shape) - 1)))
) # no noise when t == 0
sample = mean_pred + nonzero_mask * sigma * noise
return {"sample": sample, "pred_xstart": out["pred_xstart"]}
def ddim_reverse_sample(
self,
model,
x,
t,
clip_denoised=True,
denoised_fn=None,
model_kwargs=None,
eta=0.0,
):
"""
Sample x_{t+1} from the model using DDIM reverse ODE.
"""
assert eta == 0.0, "Reverse ODE only for deterministic path"
out = self.p_mean_variance(
model,
x,
t,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
model_kwargs=model_kwargs,
)
# Usually our model outputs epsilon, but we re-derive it
# in case we used x_start or x_prev prediction.
eps = (
_extract_into_tensor(self.sqrt_recip_alphas_cumprod, t, x.shape) * x
- out["pred_xstart"]
) / _extract_into_tensor(self.sqrt_recipm1_alphas_cumprod, t, x.shape)
alpha_bar_next = _extract_into_tensor(self.alphas_cumprod_next, t, x.shape)
# Equation 12. reversed
mean_pred = (
out["pred_xstart"] * th.sqrt(alpha_bar_next)
+ th.sqrt(1 - alpha_bar_next) * eps
)
return {"sample": mean_pred, "pred_xstart": out["pred_xstart"]}
def ddim_sample_loop(
self,
model,
shape,
noise=None,
clip_denoised=True,
denoised_fn=None,
model_kwargs=None,
device=None,
progress=False,
eta=0.0,
):
"""
Generate samples from the model using DDIM.
Same usage as p_sample_loop().
"""
final = None
for sample in self.ddim_sample_loop_progressive(
model,
shape,
noise=noise,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
model_kwargs=model_kwargs,
device=device,
progress=progress,
eta=eta,
):
final = sample
return final["sample"]
def ddim_sample_loop_progressive(
self,
model,
shape,
noise=None,
clip_denoised=True,
denoised_fn=None,
model_kwargs=None,
device=None,
progress=False,
eta=0.0,
):
"""
Use DDIM to sample from the model and yield intermediate samples from
each timestep of DDIM.
Same usage as p_sample_loop_progressive().
"""
if device is None:
device = next(model.parameters()).device
assert isinstance(shape, (tuple, list))
if noise is not None:
img = noise
else:
img = th.randn(*shape, device=device)
indices = list(range(self.num_timesteps))[::-1]
if progress:
# Lazy import so that we don't depend on tqdm.
from tqdm.auto import tqdm
indices = tqdm(indices)
for i in indices:
t = th.tensor([i] * shape[0], device=device)
with th.no_grad():
out = self.ddim_sample(
model,
img,
t,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
model_kwargs=model_kwargs,
eta=eta,
)
yield out
img = out["sample"]
def _vb_terms_bpd(
self, model, x_start, x_t, t, clip_denoised=True, model_kwargs=None
):
"""
Get a term for the variational lower-bound.
The resulting units are bits (rather than nats, as one might expect).
This allows for comparison to other papers.
:return: a dict with the following keys:
- 'output': a shape [N] tensor of NLLs or KLs.
- 'pred_xstart': the x_0 predictions.
"""
true_mean, _, true_log_variance_clipped = self.q_posterior_mean_variance(
x_start=x_start, x_t=x_t, t=t
)
out = self.p_mean_variance(
model, x_t, t, clip_denoised=clip_denoised, model_kwargs=model_kwargs
)
kl = normal_kl(
true_mean, true_log_variance_clipped, out["mean"], out["log_variance"]
)
kl = mean_flat(kl) / np.log(2.0)
decoder_nll = -discretized_gaussian_log_likelihood(
x_start, means=out["mean"], log_scales=0.5 * out["log_variance"]
)
assert decoder_nll.shape == x_start.shape
decoder_nll = mean_flat(decoder_nll) / np.log(2.0)
# At the first timestep return the decoder NLL,
# otherwise return KL(q(x_{t-1}|x_t,x_0) || p(x_{t-1}|x_t))
output = th.where((t == 0), decoder_nll, kl)
return {"output": output, "pred_xstart": out["pred_xstart"]}
def training_losses(self, model, x_start, t, model_kwargs=None, noise=None):
"""
Compute training losses for a single timestep.
:param model: the model to evaluate loss on.
:param x_start: the [N x C x ...] tensor of inputs.
:param t: a batch of timestep indices.
:param model_kwargs: if not None, a dict of extra keyword arguments to
pass to the model. This can be used for conditioning.
:param noise: if specified, the specific Gaussian noise to try to remove.
:return: a dict with the key "loss" containing a tensor of shape [N].
Some mean or variance settings may also have other keys.
"""
if model_kwargs is None:
model_kwargs = {}
if noise is None:
noise = th.randn_like(x_start)
x_t = self.q_sample(x_start, t, noise=noise)
terms = {}
if self.loss_type == LossType.KL or self.loss_type == LossType.RESCALED_KL:
terms["loss"] = self._vb_terms_bpd(
model=model,
x_start=x_start,
x_t=x_t,
t=t,
clip_denoised=False,
model_kwargs=model_kwargs,
)["output"]
if self.loss_type == LossType.RESCALED_KL:
terms["loss"] *= self.num_timesteps
elif self.loss_type == LossType.MSE or self.loss_type == LossType.RESCALED_MSE:
model_output = model(x_t, self._scale_timesteps(t), **model_kwargs)
if self.model_var_type in [
ModelVarType.LEARNED,
ModelVarType.LEARNED_RANGE,
]:
B, C = x_t.shape[:2]
assert model_output.shape == (B, C * 2, *x_t.shape[2:])
model_output, model_var_values = th.split(model_output, C, dim=1)
# Learn the variance using the variational bound, but don't let
# it affect our mean prediction.
frozen_out = th.cat([model_output.detach(), model_var_values], dim=1)
terms["vb"] = self._vb_terms_bpd(
model=lambda *args, r=frozen_out: r,
x_start=x_start,
x_t=x_t,
t=t,
clip_denoised=False,
)["output"]
if self.loss_type == LossType.RESCALED_MSE:
# Divide by 1000 for equivalence with initial implementation.
# Without a factor of 1/1000, the VB term hurts the MSE term.
terms["vb"] *= self.num_timesteps / 1000.0
target = {
ModelMeanType.PREVIOUS_X: self.q_posterior_mean_variance(
x_start=x_start, x_t=x_t, t=t
)[0],
ModelMeanType.START_X: x_start,
ModelMeanType.EPSILON: noise,
}[self.model_mean_type]
assert model_output.shape == target.shape == x_start.shape
terms["mse"] = mean_flat((target - model_output) ** 2)
if "vb" in terms:
terms["loss"] = terms["mse"] + terms["vb"]
else:
terms["loss"] = terms["mse"]
else:
raise NotImplementedError(self.loss_type)
return terms其中几个主要的函数总结如下:
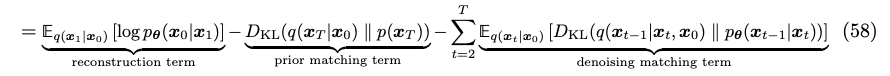
这部分代码其实就是把流程,和上面的公式做实现
- q_sample:实现的从x0到xt扩散过程;
- q_posterior_mean_variance:实现的是后验分布的均值和方差的计算公式;
- predict_start_from_noise:q_sample的逆过程,根据预测的噪音来生成;
- p_mean_variance:根据预测的噪音来计算的均值和方差;
- p_sample:单个去噪step;
- p_sample_loop:整个去噪音过程,即生成过程。
5.损失函数定义
论文loss是每个step中,真实加入的噪声和训练网络预测的噪声差值最小化。openai开源实现代码是计算实际噪声loss分布和预测噪声loss的kl散度。

def normal_kl(mean1, logvar1, mean2, logvar2):
"""
Compute the KL divergence between two gaussians.
Shapes are automatically broadcasted, so batches can be compared to
scalars, among other use cases.
"""
tensor = None
for obj in (mean1, logvar1, mean2, logvar2):
if isinstance(obj, th.Tensor):
tensor = obj
break
assert tensor is not None, "at least one argument must be a Tensor"
# Force variances to be Tensors. Broadcasting helps convert scalars to
# Tensors, but it does not work for th.exp().
logvar1, logvar2 = [
x if isinstance(x, th.Tensor) else th.tensor(x).to(tensor)
for x in (logvar1, logvar2)
]
return 0.5 * (
-1.0
+ logvar2
- logvar1
+ th.exp(logvar1 - logvar2)
+ ((mean1 - mean2) ** 2) * th.exp(-logvar2)
)6.串接训练流程
def main():
args = create_argparser().parse_args()
dist_util.setup_dist()
logger.configure()
logger.log("creating model and diffusion...")
model, diffusion = create_model_and_diffusion(
**args_to_dict(args, model_and_diffusion_defaults().keys())
)
model.to(dist_util.dev())
schedule_sampler = create_named_schedule_sampler(args.schedule_sampler, diffusion)
logger.log("creating data loader...")
data = load_data(
data_dir=args.data_dir,
batch_size=args.batch_size,
image_size=args.image_size,
class_cond=args.class_cond,
)
logger.log("training...")
TrainLoop(
model=model,
diffusion=diffusion,
data=data,
batch_size=args.batch_size,
microbatch=args.microbatch,
lr=args.lr,
ema_rate=args.ema_rate,
log_interval=args.log_interval,
save_interval=args.save_interval,
resume_checkpoint=args.resume_checkpoint,
use_fp16=args.use_fp16,
fp16_scale_growth=args.fp16_scale_growth,
schedule_sampler=schedule_sampler,
weight_decay=args.weight_decay,
lr_anneal_steps=args.lr_anneal_steps,
).run_loop()小结
1.把DDIM模型做了实现层面的介绍
2.把具体实现代码和推导细节对应
3.代码学习是为了后面sd模型打基础
4.甚至是为了后续改模型架构,增加更多特征信息作铺垫

![[JAVA EE]创建Servlet——继承HttpServlet类笔记2](https://img-blog.csdnimg.cn/63dec33eb8fb43078f994eaccca3c93f.png)
![[前端基础]websocket协议](https://img-blog.csdnimg.cn/8d13bc87c4854523bf94b119db37b7e3.png)