目录

 

一.问题描述

描述

 二.示例

三.动态规划方法

（一）最优子结构

 （二）递推关系建立

 （三）自底向上计算

（四）代码实现

---

一.问题描述

描述

输入一个长度为n的整型数组array，数组中的一个或连续多个整数组成一个子数组，子数组最小长度为1。求所有子数组的和的最大值。

数据范围:

1<=n<=2×1051<=n<=2×105

−100<=a[i]<=100−100<=a[i]<=100

要求:时间复杂度为 O(n)O(n)，空间复杂度为 O(n)O(n)

进阶:时间复杂度为 O(n)O(n)，空间复杂度为 O(1)O(1)

 二.示例

输入：

[1,-2,3,10,-4,7,2,-5]

返回值：

18

说明：

经分析可知，输入数组的子数组[3,10,-4,7,2]可以求得最大和为18        

该问题有多种解决方法，本文使用动态规划方法。

三.动态规划方法

（一）最优子结构

原数组

记录相加后的数组

 假设原始答案为ar[0],计算ar[0]和ar[0]+ar[1]哪个大，如果后者大，将其值存入数组，否则新数组该位仍为ar[0]。

选取子问题里面的最优解即和最大。

依次得到数组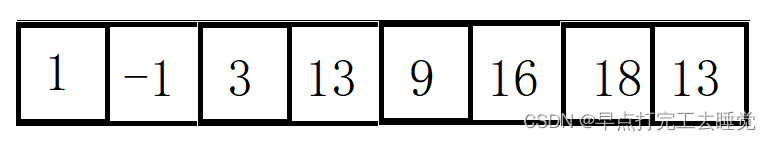

 （二）递推关系建立

 （三）自底向上计算

因为新数组保存的是每次得到的最优解，遍历该数组得到最大的数，就是该问题的解。

（四）代码实现

/**
 * 
 * @param array int整型一维数组 
 * @param arrayLen int array数组长度
 * @return int整型
 */
int FindGreatestSumOfSubArray(int* array, int arrayLen ) {
    int*d=(int*)malloc(sizeof(int)*arrayLen);
    if(arrayLen==1){
        return array[0];
    }
    d[0]=array[0];
    for(int i=1;i<arrayLen;i++){
        int a=array[i];
        int b=array[i]+d[i-1];
        d[i]=a>b?a:b;
    }
    int max=d[0];
    for(int i=0;i<arrayLen;i++){
        if(max<d[i]){
            max=d[i];
        }
    }
    return max;
}

本题链接：连续子数组的最大和_牛客题霸_牛客网

最近小白会刷一些题，与大家分享下小白的思路。