区间信息维护与查询【线段树】 - 原理2 线段树中的“懒操作”

news2024/11/27 4:13:53

区间信息维护与查询【线段树】 - 原理2 线段树中的“懒操作”

之前我们已经说了对线段树的点更新和区间查询，若要求对区间中的所有点都进行更新，该怎么办？

若对区间的每个点都进行更新，则时间复杂度较高，可以引入懒操作。下面讲解带有懒标记的区间更新和区间查询操作。

【1】区间更新

对[l , r ]区间进行更新，例如将[l , r ]区间的所有元素都更新为v ，步骤如下。

① 若当前节点的区间被查询区间[l , r ]覆盖，则仅对该节点进行更新并做懒标记，表示该节点已被更新，对该节点的子节点暂不更新。

② 判断是在左子树中查询还是在右子树中查询。在查询过程中，若当前节点带有懒标记，则将懒标记下传给子节点（将当前节点的懒标记清除，将子节点更新并做懒标记），继续查询。

③ 在返回时更新最值。

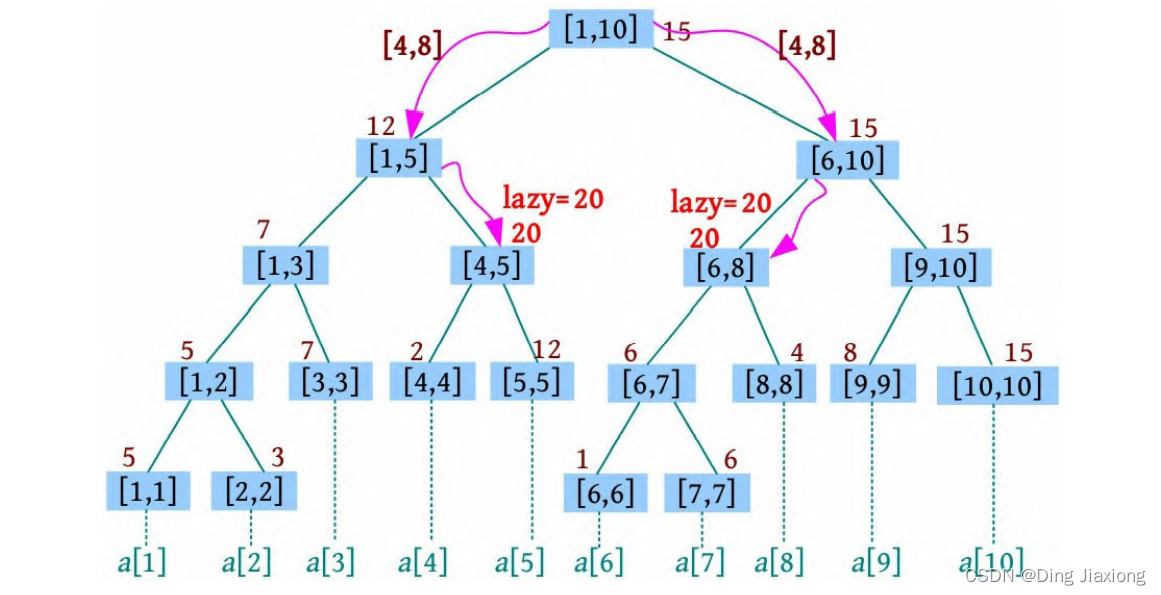
例如，在[1, 10]区间的线段树中修改[4, 8]区间的值为20，其过程如下。

① 先判断[4, 8]区间是否覆盖树根区间[1, 10]，树根划分点mid=(1+10)/2=5，查询区间横跨树根的左右子树区间，分别到左右子树中查找区间[4, 8]，若当前节点有懒标记，则下传懒标记。

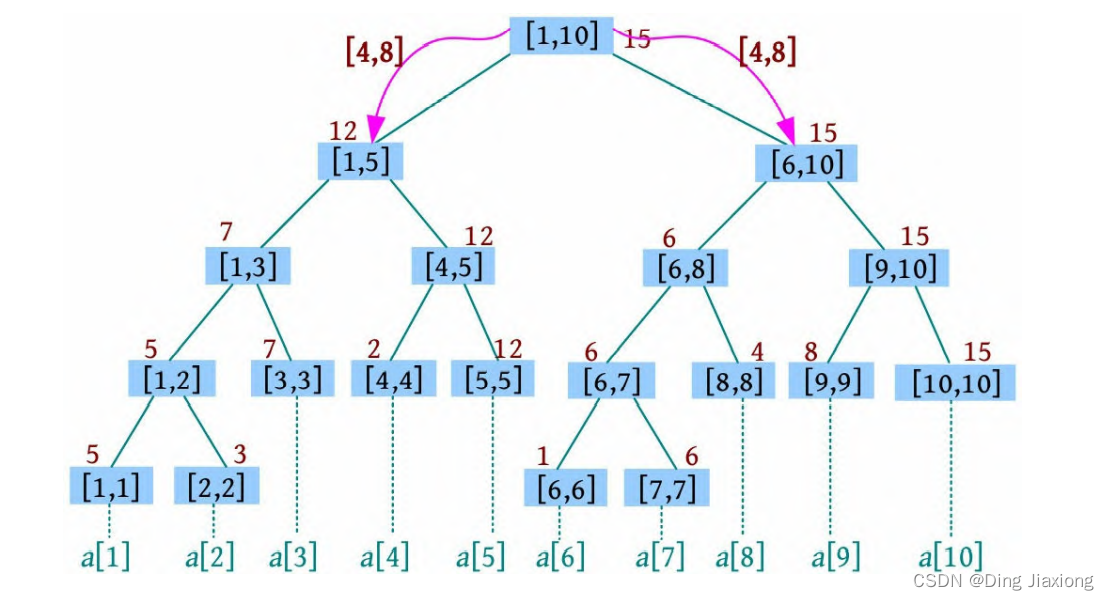
在这里插入图片描述

② 在左子树[1, 5]中查找更新区间[4, 8]，划分点mid=(1+5)/2=3，查询区间在右子树中，到右子树[4, 5]中查找区间[4,8]，若该节点有懒标记，则下传懒标记。更新区间[4, 8]正好覆盖[4,5]区间，更新最值并做懒标记。

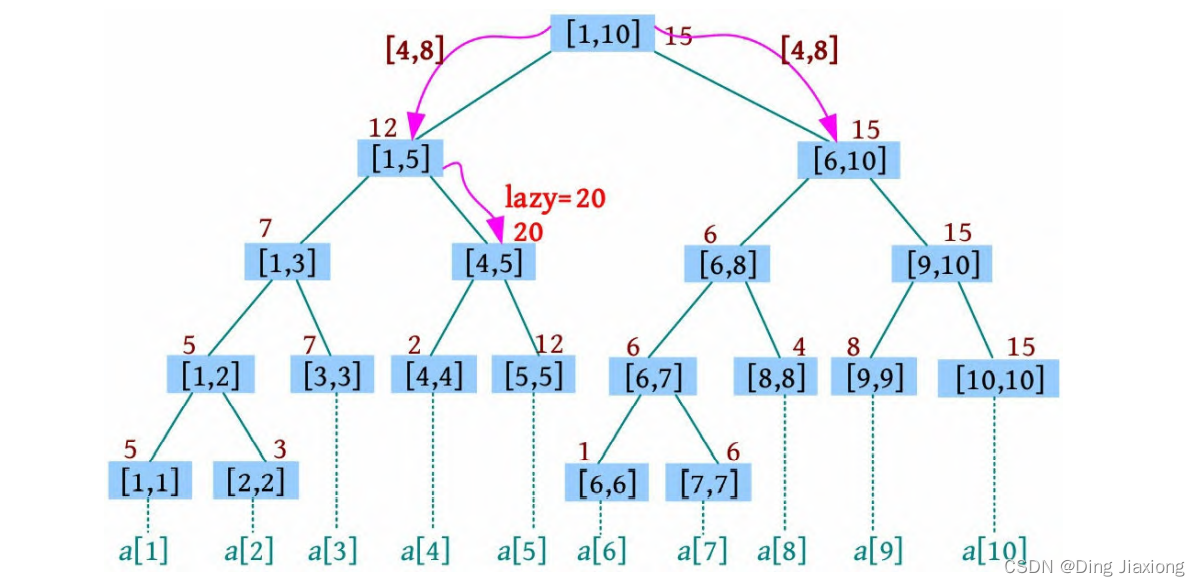
在这里插入图片描述

③ 在右子树[6, 10]中查找更新区间[4, 8]，划分点mid=(6+10)/2=8，查询区间在左子树中，到左子树[6, 8]中查找更新区间[4, 8]，若该节点有懒标记，则下传懒标记。更新区间[4, 8]正好覆盖[6, 8]区间，更新最值并做懒标记。

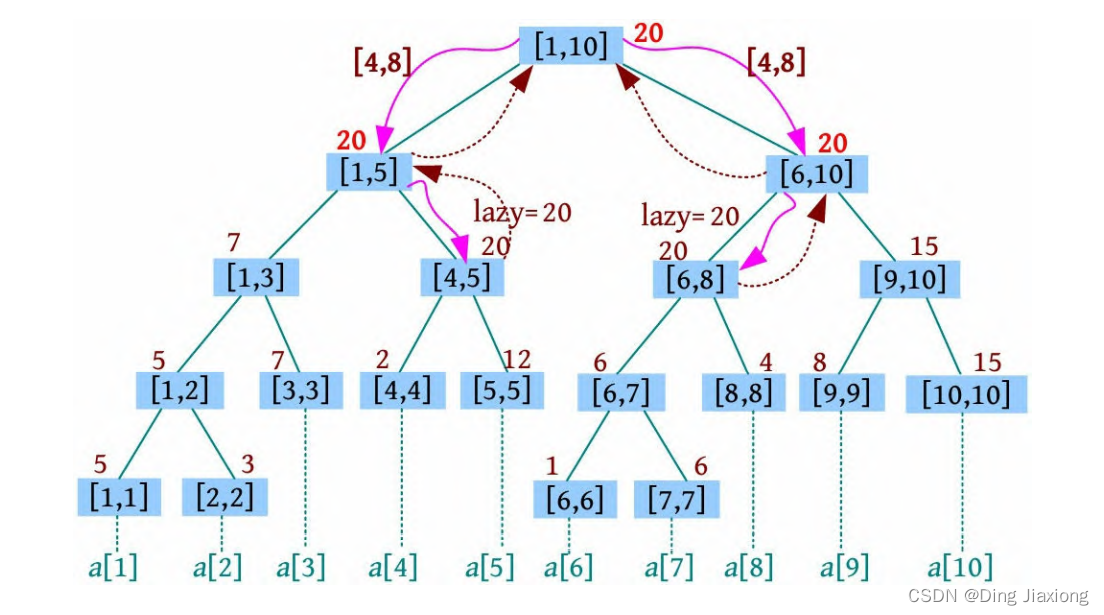
在这里插入图片描述

④ 返回时，更新节点的最值为其左右子树最值的最大值。

在这里插入图片描述

[算法代码]

void lazy(int k , int v){
	tree[k].mx = v; //更新最值
	tree[k].lz = v; //做懒标记
}

void pushdown(int k){ // 向下传递懒标记
	
	lazy(2 * k , tree[k].lz); // 下传给左子节点
	lazy(2 * k + 1, tree[k].lz); //下传给 右子节点
	tree[k].lz = -1; //清除自己的 懒标记
}

void update(int k , int l , int r , int v){ //将[l ,r ] 区间的所有元素 都更新为 v
	
	if(tree[k].l >= l && tree[k].r <= r){ // 找到该区间
		return lazy(k , v); // 更新并做懒标记
	}	
	if(tree[k].lz != -1){
		pushdown(k); // 懒标记下传
	}
	
	int mid , lc ,rc ;
	mid = (tree[k].l + tree[k].r) / 2; // 划分点
	lc = k * 2; //左子节点的存储下标
	rc = k * 2 + 1; //右子节点的存储下标
	
	if(l <= mid){
		update(lc , l , r ,v); //到左子树中更新
	}
	if(r > mid){
		update(rc , l , r, v); //到右子树中更新
	}
	tree[k].mx = max(tree[lc].mx , tree[rc].mx); //返回时更新最值
}

【2】区间查询

带有懒标记的区间查询和普通的区间查询有所不同，在查询过程中若遇到节点有懒标记，则下传懒标记，继续查询。

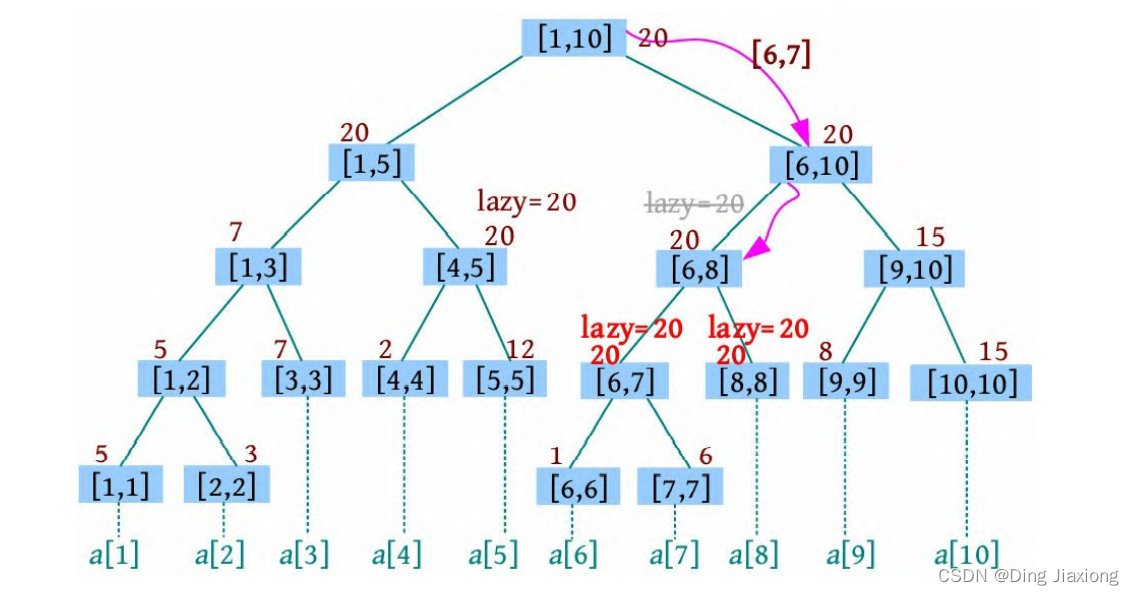
例如，查询[6, 7]区间的最值，过程如下。

① 求树根[1, 10]的划分点，mid=(1+10)/2=5，查询区间[6, 7]在右子树中，继续判断，经过[6, 8]区间时，该节点有懒标记，则下传懒标记（当前节点的懒标记清除，下传至左右子节点）。

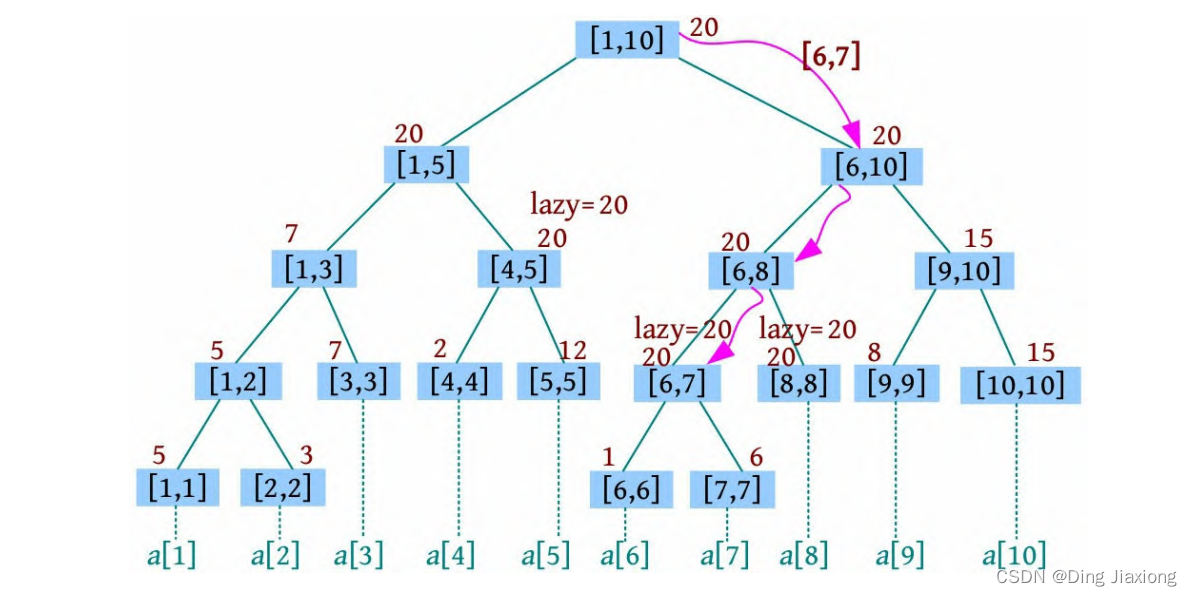
在这里插入图片描述

② 继续判断，找到[6, 7]区间，返回该区间的最值即可。

在这里插入图片描述

[算法代码]

int query(int k , int l , int r){ // 求[l .. r] 区间的最值
	
	int Max = -inf;
	if(tree[k].l >= l && tree[k].r <= r){ // 找到该区间
		return tree[k].mx;
	}
	if(tree[k].lz != -1){
		pushdown(k); //懒标记下传
	}
	
	int mid , lc , rc;
	mid = (tree[k].l + tree[k].r) / 2; //划分点
	
	lc = k * 2; // 左子节点的 存储下标
	rc = k * 2 + 1; //右子节点 的存储下标
	
	if(l <= mid){
		Max = max(Max , query(lc , l , r)); //到左子树中查询
	}
	if(r > mid){
		Max = max(Max , query(rc, l , r)); // 到右子树中查询
	}
	
	return Max;
}